Поляризация диэлектриков. Поляризованность. Поляризационные заряды. Теорема Гаусса для диэлектриков. Электрическое смещение. реферат 1. Поляризация диэлектриков. Поляризованность. Поляризационные заряды. Теорема Гаусса для диэлектриков. Электрическое смещение. Граничные условия
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Реферат на тему: Поляризация диэлектриков. Поляризованность. Поляризационные заряды. Теорема Гаусса для диэлектриков. Электрическое смещение. Граничные условия. Поляризация диэлектриков Поляризация – состояние диэлектрика, при котором элементарный объем материала приобретает электрический момент (под действием электрического поля, механических напряжений или спонтанно в сегнетоэлектриках). Виды поляризации диэлектриков: Быстрые поляризации Это упругие поляризации, которые происходят практически мгновенно, без рассеяния энергии приложенного электрического поля, то есть без выделения тепла в диэлектрике. Быстрые поляризации, обусловленные упруго связанными частицами. Электронная поляризация Электронная поляризация – это смещение электронного облака относительно центра ядра атома или иона (рисунок 1). Наблюдается во всех без исключения диэлектриках. Единственным видом поляризации электронная поляризация является в неполярных диэлектриках. Время протекания поляризации 10-14– 10-15с. 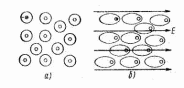 Рис. 1 Упрощенная схема электронной поляризации У неполярных диэлектриков 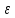 уменьшается из-за теплового расширения диэлектрика и уменьшения числачастиц в единице объема (рисунок 2). уменьшается из-за теплового расширения диэлектрика и уменьшения числачастиц в единице объема (рисунок 2).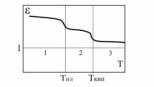 Рис. 2. Зависимость диэлектрической проницаемости от температуры для неполярных диэлектриков. У неполярных диэлектриков на частотах порядка 1014– 1016 Гц. Наблюдается резонансная дисперсия 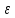 связанная с резонансной поляризацией (рисунок 3). связанная с резонансной поляризацией (рисунок 3).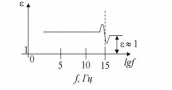 Рис. 3. Зависимость диэлектрической проницаемости от частоты для неполярных диэлектриков Ионная поляризация Ионная поляризация проявляется в смещении друг относительно друга упруго связанных разноименно заряженных ионов на расстояния меньше периода кристаллической решетки (рисунок 4). Время ионной поляризации на 2 – 3 порядка больше электронной поляризации. 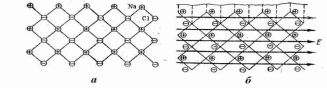 Рис. 4. Идеализированная схема расположения ионов каменной соли: а — в узлах решетки в отсутствие электрического поля, б — смещенные из узлов на небольшие расстояния при воздействии поля. Диэлектрическая проницаемость увеличивается с ростом температуры для неорганических стекол различного состава, для керамического материала - электротехнического фарфора, содержащего большое количество стекловидной фазы. Замедленные поляризации Это релаксационные поляризации, которые происходят не мгновенно, с рассеянием (потерями) энергии приложенного электрического поля, с выделением тепла в материале. Замедленные поляризации, обусловленные слабо связанными частицами. Дипольно-релаксационная поляризация При дипольной поляризации диполи ориентируются под действием поля. Увеличение температуры приводит к ослаблению молекулярных сил вследствие чего поляризация может усилиться (рисунок 5), но при этом растет энергия теплового движения молекул и ориентирующее влияние поля уменьшается, приводя к спаду проницаемости. Зависимость диэлектрической проницаемости от частоты для жидкого полярного диэлектрика при различных температурах показана на рисунке 6. После некоторой частоты диполи не успевают ориентироваться по полю и диэлектрическая проницаемость уменьшается. 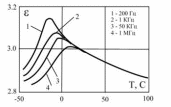 Рис. 5. Зависимость диэлектрической проницаемости полифенилсилоксановой жидкости от температуры для различных частот. 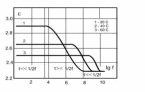 Рис. 6. Зависимость диэлектрической проницаемости от частоты жидкого полярного диэлектрика при различных температурах. Ионно-релаксационная поляризация Ионно-релаксационная поляризация наблюдается в диэлектриках с ионным типом химических связей. Слабо связанные ионы вещества под действием приложенного электрического поля смещаются на расстояния, превышающие постоянную кристаллической решетки. Электронно-релаксационная поляризация Электронно-релаксационная поляризация характерна для твердых диэлектриков, содержащих дефекты или примесные ионы, способные захватывать электроны. Такие электроны или дырки при отсутствии электрического поля могут под действием тепловых флуктуаций переходить из одного вероятного положения в другое. Время релаксации данного механизма поляризации при комнатной температуре 10-2 – 10-7с. Этот вид поляризации существенную роль играет в поликристаллической керамике типа рутила TiO2, перовскита CaTiO3, в керамических материалах, изготовленных на основе сложных оксидов титана, циркония, ниобия, тантала, свинца, церия, висмута. Миграционная поляризация Миграционная поляризация наблюдается в неоднородных диэлектриках, имеющих проводящие и полупроводящие включения, слои с различной проводимостью и т.п. При внесении неоднородных диэлектриков в электрическое поле свободные заряды смещаются и концентрируются на граничных слоях включений, в приэлектродных слоях и т.д., образуя пространственные заряды, поле которых внешне проявляет себя как "дополнительный" механизм поляризации. Спонтанная поляризация Фазовые переходы, при которых неполярные вещества самопроизвольно (спонтанно) переходят в полярное состояние называют сегнетоэлектрическими, а сам процесс перехода в новое состояние спонтанной поляризацией. Для сегнетоэлектриков характерны зависимости диэлектрической проницаемости от температуры с резко выраженным максимумом, который наблюдается вблизи точки перехода - точки КюриТк (рисунок 7). 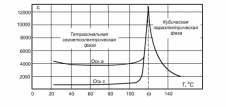 Рис. 7. Зависимость диэлектрической проницаемости от температуры вдоль осей a и c для BaTiO3 Характерные свойства сегнетоэлектриков обусловлены наличием у них доменной структуры – взаимосвязанных микрообластей, в пределах которых векторы поляризации структурных ячеек имеют одинаковое направление. Поляризованность Два одинаковых по модулю разноимённых заряда характеризуют величиной, которая называется дипольным моментом, а сами заряды называют диполем. Во многих веществах молекулы являются диполем или становятся ими под действием электрического поля. Поляризо́ванность (вектор поляризации) — векторная физическая величина, равная дипольному моменту единицы объёма вещества, возникающему при его поляризации, количественная характеристика диэлектрической поляризации. 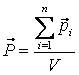 (2) (2)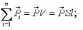 (3) (3)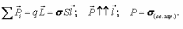 (4) (4)То есть проекция поляризованности на внешнюю нормаль равна поверхностной плотности связанных зарядов. Если диэлектрик попадает во внешнее электрическое поле, то на его гранях возникают поверхностные заряды. Поляризационные заряды В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 8). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами С другой стороны, электрический момент единицы объема равен Приравняв друг к другу оба выражения для электрического момента, получаем, что поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации: где n - единичный вектор нормали к поверхности диэлектрика. 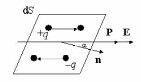 Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых Теорема Гаусса для диэлектриков Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами. Вектор напряженности Теорема Остроградского–Гаусса может быть применена в диэлектрической среде, если в правой части равенства рассматривать алгебраическую сумму всех свободных и связанных зарядов, охватываемых гауссовой поверхностью 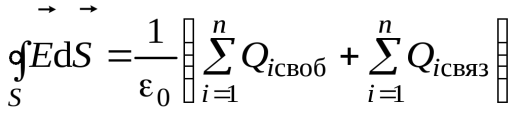 .(8) .(8)Использование полученного соотношения для расчета напряженности поля, создаваемого заданной системой свободных зарядов в диэлектрической среде, осложняется тем, что заранее не известно распределение связанных зарядов в поле. Соответственно, невозможно определить величину связанного заряда, попавшего внутрь гауссовой поверхности. Поскольку молекулы диэлектрика электрически нейтральны, то вклад в Ориентация диполей приводит к тому, что часть молекулярных зарядов при повороте диполей выходит за пределы гауссовой поверхности, а часть зарядов входит внутрь нее. Покидают объем, ограниченный гауссовой поверхностью, положительные заряды, а входят в него отрицательные. Выделим некоторый объем диэлектрика в виде косого цилиндра, образующая которого параллельна где п – концентрация молекул диэлектрика. Справа от Поскольку отрицательный и положительный заряды молекулярных диполей равны по модулю то можно определить модули “вышедших” и “вошедших” зарядов: Однако, увеличение отрицательного связанного заряда, находящегося внутри гауссовой поверхности, на С учетом полученного соотношения преобразуем выражение теоремы Остроградского–Гаусса так: 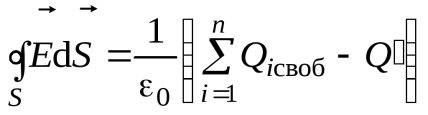 , , Последнее равенство запишем в виде: Именно в таком виде теорему Остроградского–Гаусса удобно применять в диэлектрических средах: поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охваченных этой поверхностью. При расчете напряженности электростатического поля в диэлектрической среде необходимо сначала определить модуль и направление вектора электрического смещения Повторяя рассуждения, получим: 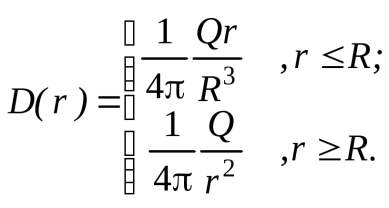 (19) (19)Так как 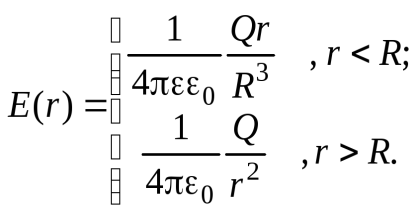 (20) (20)Отметим, что зависимость Рассмотрим физический смысл относительной диэлектрической проницаемости . Пусть в вакууме (при отсутствии диэлектрика) совокупность свободных зарядов создает электрическое поле, характеризующееся вектором Поэтому, Поскольку Электрическое смещение Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами, так что вектор напряженности E, характеризующий результирующее поле в диэлектрике, Если обозначить объемную плотность свободных зарядов в дифференциальной форме, либо в интегральной форме откуда для вектора электрического смещения (индукции) находим Последнее выражение показывает, что вектор электрической индукции учитывает поляризованность среды. Возвращаясь к соответствующим формулировкам теоремы Гаусса можно видеть, что вектор электрического смещения характеризует источники электрического поля, т. е. свободные заряды, на которых этот вектор начинается и заканчивается. Так как Напряженность электрического поля характеризует как свободные, так и связанные заряды, поэтому вектор напряженности терпит разрывы на границах областей, где присутствуют связанные заряды, например на границе раздела двух диэлектриков с различными Граничные условия Во многих случаях неоднородную среду можно представить в виде совокупности кусочно-непрерывных однородных областей, разделённых бесконечно тонкими границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая» на границах получающиеся решения. В частности, при рассмотрении решения в конечном объёме необходимо учитывать условия на границах объёма с окружающим бесконечным пространством. Граничные условия получаются из уравнений Максвелла предельным переходом. Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме. Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно получить следующую связь между компонентами поля в двух областях, примыкающих к границе: 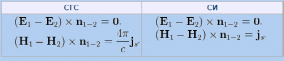 где Аналогичным образом, выбирая область интегрирования в первой паре интегральных уравнений в виде цилиндра бесконечно малой высоты, пересекающего границу раздела так, что его образующие перпендикулярны границе раздела, можно получить:  где Эти граничные условия показывают непрерывность нормальной компоненты вектора магнитной индукции (нормальная компонента электрической индукции непрерывна только при отсутствии на границе поверхностных зарядов). Из уравнения непрерывности можно получить граничное условие для токов: Важным частным случаем является граница раздела диэлектрика и идеального проводника. Поскольку идеальный проводник имеет бесконечную проводимость, электрическое поле внутри него равно нулю (иначе оно порождало бы бесконечную плотность тока). Тогда в общем случае переменных полей из уравнений Максвелла следует, что и магнитное поле в проводнике равно нулю. |
