Звук волны. Решения Задачи 7_8. Задача 7 Теория Объемная плотность энергии
 Скачать 77.79 Kb. Скачать 77.79 Kb.
|
|
Задача 7 Теория: Объемная плотность энергии - энергия колебательного движения частиц среды, содержащихся в единице ее объема: где ρ - плотность среды, А - амплитуда колебаний частиц, ω – циклическая частота волны. Формула длины волны увязывает линейную скорость распространения волны (υ) с циклическая частотой (ω) и частотой колебаний (ν)  Здесь v - скорость волны, Т - период колебаний, ν- частота колебаний точек среды, ω - циклическая частота, π – 3,14. Здесь v - скорость волны, Т - период колебаний, ν- частота колебаний точек среды, ω - циклическая частота, π – 3,14.При распространении волны энергия, сообщаемая источником, переносится в удаленные области. Для количественного описания переноса энергии вводят следующие величины. Интенсивность волны или плотность потока энергии (I) - величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны: Можно показать, что интенсивность волны равна произведению скорости ее распространения на объемную плотность энергии 7. Интенсивность плоской волны в воздухе равна 𝐼 = 10-10 Вт/м2 . Найдите амплитуду колебания частиц (молекул) воздуха при нормальных условиях и объемную плотность энергии колебательного движения для частот: ν = 20 Гц, ν = 1000Гц; ν = 20.103 Гц. Скорость звука в воздухе υ = 330 м/𝑐 . Дано: 𝐼 = 10-10 Вт/м2 Плотность воздуха при нормальных условиях: ρ = 1,2 кг/м3 ν 1 = 20 Гц; ν 2 = 1 кГц; ν 3 = 20 кГц; υ = 330 м/𝑐 Решение: ρ A2𝛚2 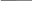 Объемная плотность энергии W = ; 𝐼 = υ . W Объемная плотность энергии W = ; 𝐼 = υ . W2 𝐼 10-10 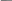  W= = = 0,3. 10-10(Дж/м3) W= = = 0,3. 10-10(Дж/м3)υ 330 Через интенсивность волны определим амплитуду колебания частиц молекул воздуха υ ρ A2𝛚2υ ρ A24 π2ν 2 𝐼 = ------------ = ------------------- = υ ρ A22π2ν2 2 2 Отсюда амплитуду колебания частиц молекул воздуха 𝐼  А2 = А2 = υ ρ 2π2 ν2 А= 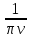 . . 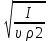 = =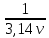 . . 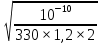 = = 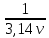 .0,0013. .0,0013.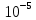 Подставляя частоту колебаний (ν), определим амплитуду для заданных частот: 0,0004. 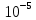  А1= = 0,00002. А1= = 0,00002.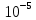 = 0,2. = 0,2.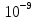 = 0,2(нм); = 0,2(нм);20 0,0004. 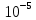  А2= = 4. А2= = 4.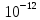 = 0,004. = 0,004.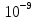 = 0,004 (нм); = 0,004 (нм);1000 0,0004. 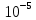  А3= = 0,2. А3= = 0,2.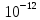 = 0,0002. = 0,0002.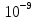 = 0,0002 (нм): = 0,0002 (нм):20000 Задача 8 Специфическое действие оказывает шум на функции органа слуха. Ухо, как и все органы чувств, способно адаптироваться к шуму. При этом под действием шума порог слышимости повышается на 10-15 дБ. После прекращения шумового воздействия нормальное значение порога слышимости восстанавливается только через 3-5 минут. При высоком уровне интенсивности шума (80-90 дБ) его утомляющее действие резко усиливается. Одной из форм расстройства функции органа слуха, связанной с длительным воздействием шума, является тугоухость. В лабораторном цехе уровень интенсивности шума достигал 80 дБ. С целью уменьшения шума было решено обить стены этого помещения материалом, поглощающим звук, который уменьшает интенсивность звука (Вт/м2) в 1000 раз. Какой уровень интенсивности шума станет после этого в этом помещении? L1 = 80 дБ J2 1   = = J1 1000 ------------------------------------- L2 = ? Решение Уровень интенсивности шума в децибелах определяется соотношением: J  L1 = 10.lg , L1 = 10.lg ,J0 где J0 – условный нулевой уровень интенсивности звука (J0 =10-12 Вт/м2). При изменении интенсивности звука изменение уровня интенсивности шума будет равно:  Отсюда, подставляя числовые значения, получим: 1  L2 = 80+ 10.lg = 80 - 10.lg1000 = 80 - 10.3= 50 (дБ) L2 = 80+ 10.lg = 80 - 10.lg1000 = 80 - 10.3= 50 (дБ)1000 lg1000 = lg (103) = 3* lg 10 = 3*1 = 3 это пояснения, в решении можно не показывать. |
