Городнова А.В.. Понятие цилиндра Рассмотрим две параллельные плоскости a и и окружность
 Скачать 289.79 Kb.
|
|
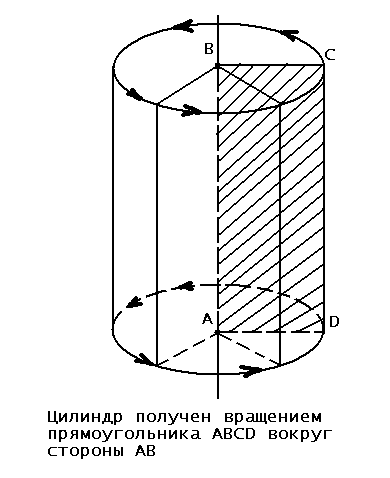§  1 ЦилиндрПонятие цилиндра Рассмотрим две параллельные плоскости a и и окружность L с центром Oрадиуса r, расположенную в плоскости (рис. 135). Через каждую точку окружности L проведём прямую, перпендикулярную к плоскости . Отрезки этих прямых, заключенные между плоскостями и , образуют цилиндрическую поверхность. Сами отрезки называются образующими цилиндрической поверхности (на рис. 135 изображены образующие АА1 , ММ1 и др.). По построению концы образующих, расположенные в плоскости , заполняют окружность L. Концы же образующих, расположенные в плоскости , заполняют окружность L1 с центром О1 радиуса r, где О1 точка пересечения плоскости  с прямой, проходящей через точку О перпендикулярно к плоскости . Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости , получается из окружности L параллельным переносом на вектор 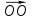 1. Параллельный перенос является движением и, значит, наложением, а при 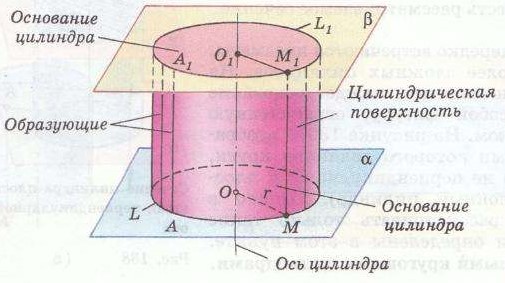 наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор 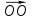1 окружность L перейдёт в равную ей окружность L1 радиуса r с центром в точке О1. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами Lи L1 , называется цилиндром (см. рис 135). Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги основаниями цилиндра. Образующие цилиндрической поверхности называются образующими цилиндра, а прямая ОО1 осью цилиндра. Все образующие цилиндра параллельны и равны друг к другу как отрезки параллельных прямых, заключенные между параллельными плоскостями и . Длина образующей называется высотой цилиндра, а радиус основания радиусом цилиндра. Ц 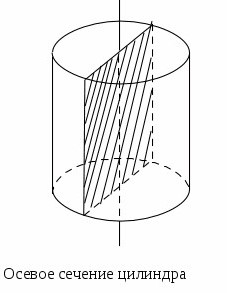 илиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке 136 изображен цилиндр, полученный вращением прямоугольника ABCD вокруг стороны AB. При этом боковая поверхность цилиндра образуется вращением стороны CD, а основания вращением сторон BC и AD.Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник (рис. 137), две стороны которого образующие, а две другие диаметры оснований цилиндра. Такое сечение называется осевым. Е 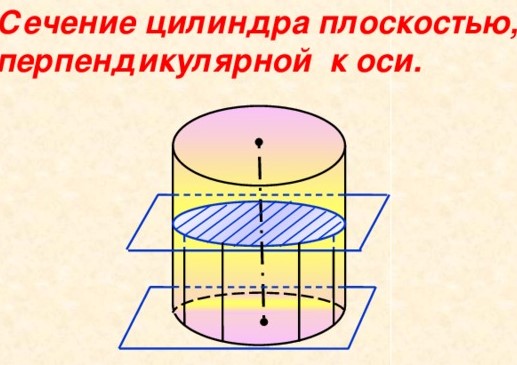 сли секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость (плоскость на рисунке 138) отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.Замечание На практике нередко встречаются предметы, которые имеют форму более сложных цилиндров. На рисунке 139, изображен цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На рисунке 139, б изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований (наклонный цилиндр). Однако в дальнейшем мы будем рассматривать только такие цилиндры, которые были определены в этом пункте. Их называют иногда прямыми круговыми цилиндрами. Площадь поверхности цилиндра  А На рисунке 140, изображен цилиндр. Представим себе, что его боковую поверхность разрезали по образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости (рис. 140, б). В результате в плоскости получится прямоугольник АВВ’А’. Стороны АВ и А’В’ прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание АА’ прямоугольника является разверткой окружности основания цилиндра, а высота АВобразующей цилиндра, поэтому АА’= 2r, АВ=h, где rрадиус цилиндра, hего высота.  a) За площадь боковой поверхности цилиндра принимается площадь её развёртки. Т 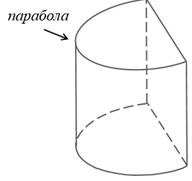 ак как площадь прямоугольника АВВ’А’ равнаАА’*AB=2rh, то для вычисления площади Sбок боковой поверхности цилиндра радиуса r и высоты h получится формула Sбок=2rh. И 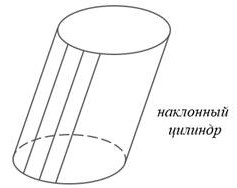 так, площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна r2, то для вычисления площади Sцил полной поверхности цилиндра получаем формулу                 окружность б) рис. 140 2r A’ B’ h A B h В Sцил=2r(r+h). |