Урок №1
Дата: 02.09.20
Класс: 10
Предмет: алгебра
Тема: Понятие действительного числа
|
Тип занятия:
|
Урок овладения новым материалом.
|
|
Цели занятия:
|
|
|
Образовательные:
|
- рассмотреть множество иррациональных чисел;
- рассмотреть множество действительных чисел;
- рассмотреть правила выполнения действий с бесконечными десятичными дробями;
- ввести понятие модуля действительного числа;
- дать определение бесконечно убывающей геометрической прогрессии
- сформировать умение нахождения суммы бесконечно убывающей геометрической прогрессии;
- сформировать желание самостоятельно изучать материал;
|
|
Воспитательные:
|
- воспитывать положительное отношение к приобретению новых знаний;
- воспитывать ответственность за свои действия и поступки;
- вызвать заинтересованность новым для студентов подходом изучения математики.
|
|
Развивающие:
|
- формировать навыки познавательного мышления;
- формировать умения и навыки учебного труда.
|
|
Методы обучения:
|
Лекция объяснительно - иллюстрированная
|
|
Планируемый результат:
|
Ученик знает:
Определение иррационального числа. Множество действительных чисел. Определение модуля действительного числа. Определение бесконечно убывающей геометрической прогрессии. Формулы геометрической прогрессии. Формулу суммы бесконечно убывающей геометрической прогрессии. Умеет выполнять действия с бесконечными десятичными дробями. Умеет находить сумму бесконечно убывающей геометрической прогрессии.
|
|
Структура занятия:
|
1. Устная работа
|
|
2. Объяснение темы «Действительные числа»
Определение иррационального числа
Множество действительных чисел
Действия с бесконечными десятичными дробями
Модуль действительного числа
|
|
3. Решение тренировочных упражнений из учебника на закрепление темы
|
|
4. Объяснение темы «Бесконечно убывающая геометрическая прогрессия»
Геометрическая прогрессия (повторение)
Основные формулы геометрической прогрессии (повторение)
Бесконечно убывающая геометрическая прогрессия
Решение ключевой задачи №1
Формула суммы бесконечно убывающей геометрической прогрессии
Решение ключевых задач №2, №3, №4
|
|
5. Решение тренировочных упражнений на закрепление темы (нечетные пункты).
6. Домашнее задание.
|
1
|
Устная работа:
|
|
Переведите в десятичную дробь:
|
Переведите в обыкновенную дробь:
|
|

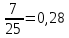

|



|
2
|
Объяснение темы «Действительные числа»:
|
|
Определение иррационального числа
|
Определение
Иррациональным числом называется бесконечная десятичная непериодическая дробь.
Иррациональные числа, как и рациональные, могут быть положительными и отрицательными.
Например, число 0,123456…., в котором после запятой записаны подряд все натуральные числа, является положительным иррациональным числом. Число -5, 246810…., в которм после запятой записаны подряд все четные числа, является отрицательным иррациональным числом.
Числа  также являются иррациональными, так как можно доказать, что они могут быть представлены в виде бесконечных десятичных непериодических дробей. также являются иррациональными, так как можно доказать, что они могут быть представлены в виде бесконечных десятичных непериодических дробей.
|
|
Множество действительных чисел
|
Рациональные и иррациональные числа образуют множество действительных чисел.

|
Действия с бесконечными десятичными дробями.
|
Известно как выполняются действия над конечными десятичными дробями. Арифметические операции над действительными числами, т.е. бесконечными десятичными дробями, заменяются операциями над их приближениями.
Например,вычислим приближенные значения 
Решение:
Воспользуемся калькулятором и найдем значения 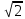 и и 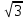
Имеем 
Найдем  с точностью до единицы с точностью до единицы
 и и  , тогда , тогда 
Найдем  с точностью до одной десятой с точностью до одной десятой
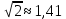 и и 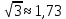 , тогда , тогда 
Найдем  с точностью до одной сотой с точностью до одной сотой
 и и 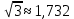 , тогда , тогда 
Анальгично, вычисляя произведение  с точностью до 0,1, получаем с точностью до 0,1, получаем

Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
|
|
Модуль действительного числа
|
Определение.
Модуль действительного числа  обозначается обозначается  и определяется так же, как и модуль рационального числа: и определяется так же, как и модуль рационального числа:

|
|
3
|
Решение тренировочных упражнений
|
|
№9. Выяснить, каким числом (рациональным или иррациональным) является числовое значение выражения:
|
|

|

|
|
Решение: Перемножим скобки
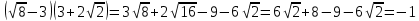
Ответ: является рациональным числом
|
Решение: Перемножим скобки

Ответ: является иррациональным числом
|
|
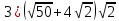
|

|
|
Решение: Раскроем скобки (распределительный закон)

Ответ: является рациональным числом
|
Решение: Раскроем скобки (распределительный закон)

Ответ: является рациональным числом
|
|
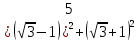
|
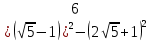
|
|
Решение: Раскроем скобки (формулы сокращенного умножения)

Ответ: является рациональным числом
|
Решение: Раскроем скобки (формулы сокращенного умножения)

Ответ: является иррациональным числом
|
|
№10. Вычислить:
|
|

|
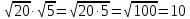
|
|
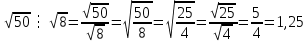
|

|
4
|
Объяснение темы «Бесконечно убывающая геометрическая прогрессия»:
|
Геометрическая прогрессия
|
Геометрической прогрессией называется такая числовая последовательность  что для всех натуральных что для всех натуральных 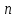 выполняется равенство выполняется равенство

Например, 
|
Основные формулы геометрической прогрессии
|
Формула 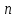 -го члена геометрической прогрессии: -го члена геометрической прогрессии:

Формула суммы 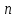 первых членов геометрической прогрессии: первых членов геометрической прогрессии:
 , если , если 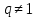
Если 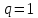 , то , то 
|
Бесконечно убывающая геометрическая прогрессия
|
Среди геометрических прогрессий особый интерес представляют бесконечно убывающие геометрические прогрессии.
Пример. Рассмотрим квадраты, изображенные на рисунке. Сторона первого квадрата равна 1, сторона второго равна 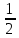 , соторна третьего , соторна третьего 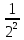 и т.д. и т.д. 
Таким образом, стороны квадратов образуют геометрическую пргрессию со знаменателем 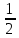 : :
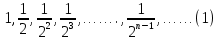
Площади этих квадратов образуют геометрическую прогрессию со знаменателем 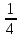

|
Из рисунка видно, что стороны квадратов и их площади с возрастанием номера 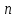 становятся все меньше, приближаясь к нулю. Поэтому каждая из прогрессий (1) и (2) называется бесконечно убывающей. становятся все меньше, приближаясь к нулю. Поэтому каждая из прогрессий (1) и (2) называется бесконечно убывающей.
Рассмотрим геометрическую прогрессию

Знаменатель этой прогрессии 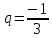 , а ее члены , а ее члены 
С возрастанием номера 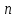 члены этой прогрессии приближаются к нулю. Эту прогрессию так же называют бесконечно убывающей. Ометим, что модуль ее знаменателя меньше единицы: члены этой прогрессии приближаются к нулю. Эту прогрессию так же называют бесконечно убывающей. Ометим, что модуль ее знаменателя меньше единицы: 
Определение.
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.
|
Решение ключевой задачи
Задача №1.
Доказать, что геометрическая прогрессия, заданная формулой -го члена 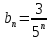 , является бесконечно убывающей. , является бесконечно убывающей.
|
Решение:
Найдем первый и второй члены заданной геометрической прогрессии:
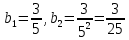
Найдем знаменатель геометрической прогрессии:

Так как модуль полученного знаменателя меньше единицы, т.е.  , то по определению данная геометрическая прогрессия является бесконечно убывающей. , то по определению данная геометрическая прогрессия является бесконечно убывающей.
|
Формула суммы бесконечно убывающей геометрической прогрессии
|
Рассмотрим квадрат состороной равной единице. Отметим штриховкой его половину, затем половину оставшейся части и т.д. Площади заштрихованных прямоугольников образуют бесконечно убывающую геометрическую прогрессию
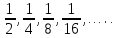

Если заштриховать все полученные таким образом прямоугольники, тоштриховкой покроется весь квадрат. Естественно считать, что сумма площадей всех заштрихованных прямоугольников равна единице, т.е.
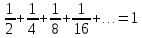
|
Выведем формулу суммы бесконечно убывающей геометрической прогрессии с помощью формулы суммы 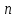 первых членов геометрической прогрессии первых членов геометрической прогрессии

Запишем ее так:
Так как  , то , то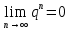 , ,  , ,
поэтому
Таким образом, сумма S бесконечно убывающей геометрической прогрессии вычисляется по формуле:
 (4) (4)
Из формулы (4) при 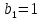 получаем получаем  . .
Это равенство обычно записывают так:

Заметим, что это равенство справедливо при  , в частности при , в частности при 
|
Решение ключевых задач
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии
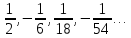
|
Решение:
Выпишем  и и  и найдем и найдем  : :

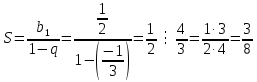
|
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии, если  , , 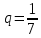
|
Решение:
Необходимо найти  , поэтому воспользуемся формулой , поэтому воспользуемся формулой 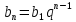 , тогда , тогда 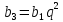
Подставим данные, 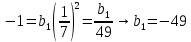

|
|
Задача №4. Записать бесконечную периодическую десятичную дробь 1,1(3) в виде обыкновенной.
|
Решение:
Число 1,1(3) можно записать в виде суммы 
Сумма слагаемых, начиная со второго, является суммой  бесконечно убывающей геометрической прогрессии. бесконечно убывающей геометрической прогрессии.
Тогда 
Получаем, 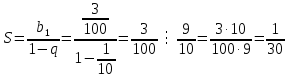
Учитывая исходные данные, получаем 1,1(3)
|
5
|
Решение тренировочных упражнений из учебника «Алгебра и начала анализа 10» на закрепление темы:
|
Найти сумму бесконечно убывающей геометрической прогрессии, если
|
 , , 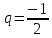
Решение:

|
 , , 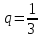
Решение:

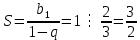
|
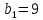 , , 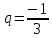
Решение:

|
 , , 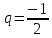
Решение:
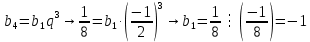

|
. Найти сумму бесконечно убывающей геометрической прогрессии
|
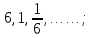
Выпишем  и и  и найдем и найдем  : :


|
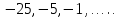
Выпишем  и и 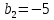 и найдем и найдем  : :
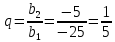

|
Записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
|
|
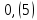
Решение:
Представим 
Сумма слагаемых является суммой  бесконечно убывающей бесконечно убывающей
геометрической прогрессии.
Тогда 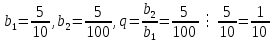
Получаем, 
Итак, 0,(5)
|

Решение:
Представим 
Сумма слагаемых является суммой  бесконечно убывающей бесконечно убывающей
геометрической прогрессии.
Тогда 
Получаем, 
Итак, 0,(8)
|
7
|
Домашнее задание: п. 1.1.- знать правила,Решение № 1.4 а), 1.5 а), 1.8 а)
|
|
| |
 Скачать 0.63 Mb.
Скачать 0.63 Mb.