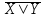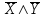лекции Логика. лекции логика. Понятие элементарного произведения. Днф, кнф Понятие элементарного произведения. Днф, кнф
 Скачать 261.47 Kb. Скачать 261.47 Kb.
|
|
Тема лекции «Понятие элементарного произведения. ДНФ, КНФ» Понятие элементарного произведения. ДНФ, КНФ Дизъюнктивная нормальная форма Отрицание, относящиеся к переменной называется тесным (простым). Отрицание, не являющееся тесным, называется сложным. Определение: Высказывательная форма называется приведенной, если она не содержит операции импликации и сложного отрицания. Определение: Высказывательная форма, состоящая из переменных или отрицания переменных с применением только одной операции дизъюнкции, называется элементарной дизъюнкцией. Определение: Высказывательная форма, состоящая из элементарных конъюнкций, с применением только одной операции дизъюнкции называется дизъюнктивной нормальной формой (ДНФ). Конъюнктивная нормальная форма Определение: Высказывательная форма, состоящая из переменных или отрицательных переменных, применением только одной операции конъюнкции, называется элементарной конъюнкцией. Определение: Высказывательная форма, состоящая из элементарных дизъюнкций, применением только одной операции конъюнкции называется конъюнктивной нормальной формой (КНФ). Более просто: ДНФ - это сумма произведений, а КНФ - это произведение логических сумм. Для нахождения ДНФ, КНФ необходимо построить таблицу истинности или упростить данную формулу. Рассмотрим на следующих занятиях Контрольные вопросы: 1. Какая форма записи высказывания называется высказывательной? 2. Какая высказывательная форма называется элементарной дизъюнкцией? 3. Какая высказывательная форма называется элементарной конъюнкцией? 4. Какая высказывательная форма называется дизъюнктивной нормальной формой (ДНФ)? 5. Какая высказывательная форма называется конъюнктивной нормальной формой (КНФ)? Закрепление нового материала: Перевод с естественного языка на формальный Задание 1. Представить высказывание в виде логической формулы: «Солнце светит тогда и только тогда, когда на небе нет туч». Решение а) Простых высказываний в данном предложении два: 1. Солнце светит, 2. На небе есть тучи. Обозначим их латинскими буквами: А – Солнце светит, В – На небе есть тучи. б) Логических связок в данном высказывании две: первая – тогда и только тогда, когда, вторая – нет. Первая соответствует операцииэквиваленции (⇔), вторая – операции отрицания ( ⎯ ). в) Делаем вывод о том, что формула имеет следующий вид: A⇔ В . г) Делаем проверку: А – Солнце светит, В – На небе есть тучи, ⇔ - операция эквиваленции (тогда и только тогда, когда), х - операция отрицания (нет). Следовательно, формулу A⇔ В можно прочитать следующим образом: Солнце светит тогда и только тогда, когда на небе нет туч. Ответ:высказывание соответствует формуле A⇔ В . Задание 2. Представить высказывание в виде логической формулы: «Неверно высказывание: книга интересная, если она дорогая, и ее скучно читать». Решение а) Простых высказываний в данном предложении три: 1. Книга интересная, 2. Книга дорогая, 3. Книгу скучно читать. Обозначим высказывания латинскими буквами: А – Книга интересная, В – Книга дорогая, С – Книгу скучно читать. б) В данном высказывании можно заметить две особенности: 1) посылка и заключение «поменялись местами» друг с другом, 2) частица то в данном предложении пропущена, но можно легко определить ее местоположение – после слова что. Логических связок в данном высказывании три: первая – неверно высказывание, вторая – если, …то, третья – и. Поскольку отрицание стоит в начале предложения, данная операция относится ко всей формуле. Первая логическая связка соответствует операции отрицания ( ⎯ ), вторая – операции импликации (=>), третья – операции конъюнкции (/\). в) На основе пунктов а) и б) делаем вывод, что формула имеет следующий вид: В ∧ С⇒ А. г) Делаем проверку: А – Книга интересная, В – Книга дорогая, С – Книгу скучно читать, => - операция импликации (если, …то), х - операция отрицания(неверно высказывание), /\. - операция конъюнкции (и). Следовательно, формулу В ∧ С⇒ А можно прочитать следующим образом: Неверно высказывание: если книга дорогая и ее скучно читать, то она интересная. Ответ:высказывание соответствует формуле В ∧ С⇒ А. Перевод с формального языка на естественный Задание 3. Представить логическую формулу в виде высказывания на русском языке: (А ∧ В)⇒С . Решение а) Присвоим логическим переменным А, В, С какое-либо высказывание: А – Пушкин А. С. – поэт, В – Пушкин А. С. – дуэлянт, С – Пушкин А. С. доживет до 70 лет. б) Логические операции заменим соответствующими логическими связками: А – Пушкин А. С. – не поэт; В – Пушкин А. С. – не дуэлянт; ∧ – и; ⇒ – Если …, то … в) Составим предложение по формуле, заменяя логические переменные заданными высказываниями, а операции – логическими связками: «Если Пушкин А. С. – не поэт и Пушкин А. С. – не дуэлянт, то Пушкин А. С. доживет до 70 лет». В соответствии с правилами русского языка, избавимся от повторяющихся слов: «Если Пушкин А. С. – не поэт и не дуэлянт, то он доживет до 70 лет». Ответ:«Если Пушкин А. С. – не поэт и не дуэлянт, то он доживет до 70 лет». Задание 4: вычислить значение логической формулы, предварительно указав порядок действий X ⇔ X ∨ Y ; Решение X ⇔ X ∨ Y X - первое действие; X ∨ Y - второе действие; X ⇔ X ∨ Y - третье действие.  Ответ:формула принимает истинное значение, когда Х – истина,Y – ложь. Во всех остальных случаях формула принимает значение ложь.  Тема 2.2. Методы минимизации алгебраических преобразований Тема лекции «Равносильные формулы. Законы логики» Равносильность формул Различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие равносильности формул. Две формулы алгебры высказываний F1 и F2называются равносильными (эквивалентными), если их таблицы истинности совпадают. Равносильность формул будем обозначать через F1≡F2. Нужно различать символы ↔ и ≡. Символ ↔ является символом формального языка, с помощью которого строятся формулы; символ ≡ заменяет слово «равносильно». Заметим, что отношение равносильности есть отношение эквивалентности. При этом справедливы утверждения: Если две ПФ равносильны и одна из них содержит переменные, которых нет в другой, то ПФ от этих переменных не зависит (такие переменные называются фиктивными). Если две ПФ равносильны, то их отрицания также равносильны. Если в двух равносильных ПФ все вхождения некоторой переменной заменить любой формулой, то полученные новые ПФ будут равносильны. Равносильности формул логики высказываний часто называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям. Перечислим наиболее важные из них: Законы логики 1.X X Закон тождества 2. 3. 4. 5. X X X , X X Законы идемпотентности 6 , Законы коммутативности , - Законы ассоциативности 8. , - Законы дистрибутивности (распределительности) 9. 10. X 1 , 11. , 12. , Законы поглощения 13. 14. . XY 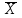 Y = Y =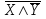 . Закон исключения импликации . Закон исключения импликации1-й закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует. Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. “Это яблоко спелое” и “Это яблоко не спелое”. Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание. Закон двойного отрицания. Отрицать отрицание какого-нибудь высказывания - то же, что утверждать это высказывание. “ Неверно, что 2× 2¹ 4” Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых “сомножителей” равносильна одному из них. Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел. В отличие от сложения и умножения чисел логическое сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции. Смысл законов де Моргана (Август де Морган (1806-1871) - шотландский математик и логик) можно выразить в кратких словесных формулировках: Доказать законы логики можно: 1) с помощью таблиц истинности; 2) с помощью равносильностей. Докажем, например, один из законов де Моргана. 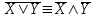 . .Для этого составим таблицы истинности для ПФ, стоящих в левой и правой частях выражения, и сравним их.
Пример. Доказать равносильность 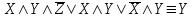 Используя закон поглощения, дистрибутивный закон и закон, определяющий действие с 1, получим 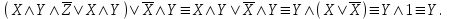 Контрольные вопросы: Объясните понятие «равносильные формулы». Сформулируйте закон тождества. Сформулируйте закон противоречия. Сформулируйте закон исключенного третьего. Сформулируйте закон двойного отрицания. Сформулируйте закон идемпотентности. Сформулируйте закон коммутативности (переместительности). Сформулируйте закон ассоциативности (сочетательности). Сформулируйте закон дистрибутивности (распределительности). Сформулируйте закон де Моргана. Сформулируйте закон поглощения. Сформулируйте закон склеивания. Сформулируйте закон исключения импликации. Сформулируйте закон эквивалентности. Сформулируйте правила действий с константами. Закрепление нового материала: Пример 1. Доказать равносильность 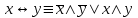 . .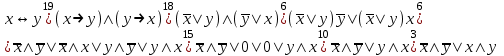 Пример 2. Упростить формулу 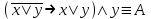 . .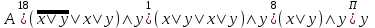 . .Пример 3. Доказать ТИ формулы 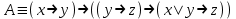 . .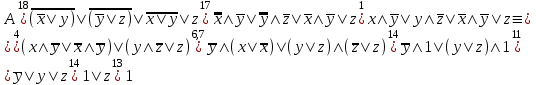 Пример 4. Доказать законы склеивания. 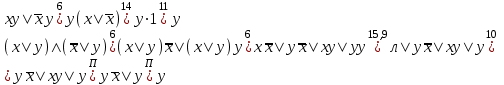 Пример 5. Доказать закон Блейка - Порецкого. 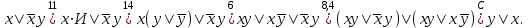 Пример 6. Доказать закон свертки логического выражения. 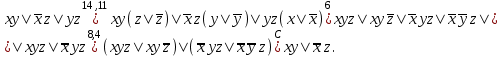 Дополнительные задачи     Тема лекции «Упрощение формул логики с помощью равносильных преобразований» Пример1. Упростите логическое выражение 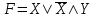 . .На первый взгляд формула не позволяет себя упростить, т.к. в ней ничего нельзя вынести за скобки. Заметим, что «хочется», чтобы у переменной Х «появился» Y. Для этого представим Х как X&1, а 1 распишем по закону исключенного третьего как Y 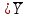 . Далее раскроем скобки. . Далее раскроем скобки.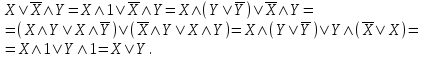 Пример2. Упростите логическое выражение 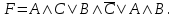 Один из возможных вариантов упрощения состоит в том, чтобы добавить к последнему слагаемому переменную С. Это делается стандартным способом: умножить А&В на 1, а 1 расписать как 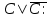 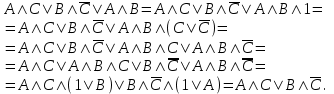 Закрепление нового материала: Пример3. Упростите логическое выражение 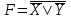 . .Применим закон де Моргана: 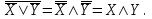 Пример4. Упростите логическое выражение 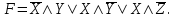 В данном случае воспользуемся законом двойного отрицания. 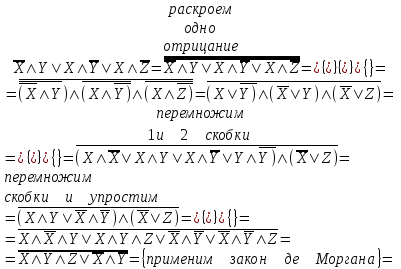 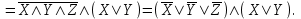 Пример5. Упростите логическое выражение 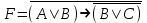 Избавимся от импликации и отрицания. Воспользуемся законом де Моргана 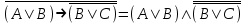 . .Применим закон двойного отрицания. Получим: 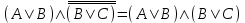 . .Применим правило дистрибутивности. Получим: 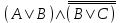 = =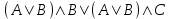 . .Применим закон коммутативности дистрибутивности. Получим: 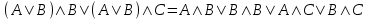 . .Применим закон идемпотентности. Получим: 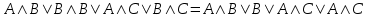 . .Применим правило дистрибутивности, т.е. вынесем за скобки В. Получим: 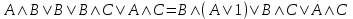  . .Применим свойство констант. Получим: 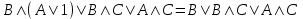 . .Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим: 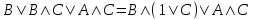 . .Применим свойство констант: 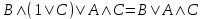 . . Задание . Упростить логические выражения: 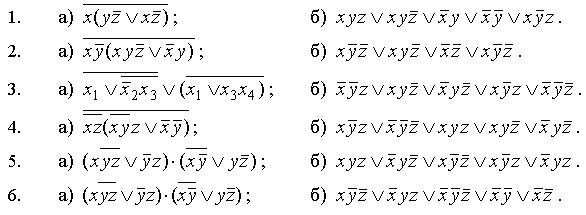 7. а) 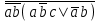 б) б) 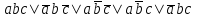 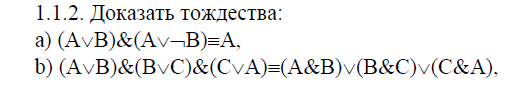 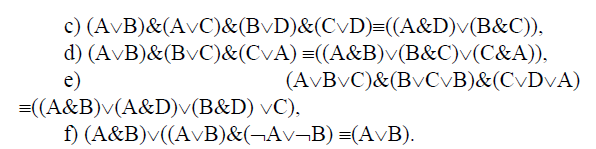 Проверьте следующие равносильности двумя способами: построив таблицу истинности и упростив выражения.   Закрепление нового материала: Проверьте следующие равносильности двумя способами: построив таблицу истинности и упростив выражения. A B V A B C V B A C V A C = A B C V A B C V A C D V A C D V C A D = A V C A B V A B (C V D)= A B A V B (A V B) C D = A A V B V (A V B) C D= A V B V C D (A V B) (A V B V C) = A V B (A B V A B C V B C V C) (C V A C V A B C) =BVAC |