Билеты (маленький шрифт). Понятие эвм и ее основных характеристик структура, архитектура
 Скачать 434.18 Kb. Скачать 434.18 Kb.
|
|
II         каналы каналы   УУВП HD HL УУВП HD HL III IV  ВНУ V I логический уровень. Процессор-Процессор Связь обеспечивается через блоки прямого управления. Один процессор выдает другому команду - сигнал. Этот канал не предназначается для обмена большими порциями информации, а только командами. II уровень общей оперативной памяти. В качестве сопрягаемых устройств используются коммутаторы многооболочной ОП. Однако при большом числе комплексирующих процессоров оперативная память становится источником большого числа конфликтов. Особо опасны конфликты когда, когда один хочет прочесть информацию а другой -поменять данные. Этот вид взаимодействия наиболее оперативный при небольшом числе обслуживаемых абонентов. III уровень комплексируемых каналов ввода-вывода. Предназначается для передачи больших объемов информации между блоками ОП, сопрягаемых в ВС. Обмен данными между ЭВМ осуществляется с помощью адаптера "канал-канал" (АКК) и команд "чтение" и "запись". Скорость передачи данных измеряется Мбайтами в секунду. Передача данных идет параллельно вычислениям в процессорах. IV уровень групповых устройств управления периферией. В качестве средств сопряжения используются двуканальные переключатели, позволяющие группы устройств подключать к каналам различных ЭВМ. Для исключения конфликтов было принято следующее: канал, перехватывающий управление, резервирует подключенное устройство до полного завершения работ. Только после освобождения ресурса эти устройства могут быть переключены на другой канал. V уровень внешних общих устройств. Предполагается, что комплексируемые внешние устройства имеют встроенный или навесной двуканальный переключатель для подключения к различным каналам. Этот уровень используется только в специальных системах. I, III, IV уровни предназначены для создания многомашинных систем. II - для многопроцессорных систем. На практике зачастую создается комбинация уровней, что позволяет создать достаточно гибкие и перестраиваемые структуры. Классификация вычислительных систем. Большое разнообразие вычислительных систем породило естественное желание ввести для них какую-то классификацию. Эта классификация должна однозначно относить ту или иную вычислительную систему к некоторому классу, который, в свою очередь, должен достаточно полно ее характеризовать. Таких попыток предпринималось множество. Одна из первых классификаций, ссылки на которую наиболее часто встречаются в литературе, была предложена М. Флинном в конце 60-х годов прошлого века. Она базируется на понятиях двух потоков: команд и данных. На основе числа этих потоков выделяется четыре класса архитектур: SISD (Single Instruction Single Data) - единственный поток команд и единственный поток данных. По сути дела это классическая машина фон Неймана. К этому классу относятся все однопроцессорные системы. SIMD (Single Instruction Multiple Data) - единственный поток команд и множественный поток данных. Типичными представителями являются матричные компьютеры, в которых все процессорные элементы выполняют одну и ту же программу, применяемую к своим (различным для каждого ПЭ) локальным данным. Некоторые авторы к этому классу относят и векторно-конвейерные компьютеры, если каждый элемент вектора рассматривать как отдельный элемент потока данных. MISD (Multiple Instruction Single Date) - множественный поток команд и единственный поток данных. М. Флинн не смог привести ни одного примера реально существующей системы, работающей на этом принципе. Некоторые авторы в качестве представителей такой архитектуры называют векторно-конвейерные компьютеры, однако такая точка зрения не получила широкой поддержки. MIMD (Multiple Instruction Multiple Date) - множественный поток команд и множественный поток данных. К этому классу относятся практически все современные многопроцессорные системы. Архитектура ВС. Параллелизм команд и данных. Архитектура ВС — совокупность характеристик и параметров, определяющих функционально-логическую и структурную организацию системы. Понятие архитектуры затрагивает более общую классификацию, относящуюся к видам параллельной обработки информации. Среди различных видов классификаций выделяют следующую классификацию. Согласно её все ВС сети могут быть разбиты на 4 группы: одиночный поток команд и данных ОКОД (SISD) множественный поток команд, одиночный поток данных МКОД (MISD) одиночный поток команд, множественный поток данных ОКМД (SIMD) множественный поток команд, множественный поток данных МКМД (MIMD). В основу данной классификации положен параллелизм обработки команд и данных, а также их сочетание. Архитектура ОКОД охватывает все однопроцессорные и одно - машинные варианты систем, т.е. с одним вычислителем, т.е. все ЭВМ классической структуры попадают в этот класс. Параллелизм обеспечиваемый этой структурой визуальный (кажущийся). Здесь параллелизм вычислений обеспечивается путем совмещения выполнения операций отдельными блоками АЛУ, а также параллельной работой устройств вывода-ввода информации и процессора. Процессор может обрабатывать только одну задачу, но параллельно вычислениям в процессоре могут выполняться операции ввода вывода. Сейчас эти системы относятся к классическим структурам ЭВМ. Архитектура МКОДпредлагает построение своеобразного процессорного конвейера, в котором результаты обработки предлагаются от одного процессора к другому по цепочке. В современных ЭВМ по этому принципу реализована схема совмещения операций, в которой параллельно работают различные функциональные блоки, и каждый из них делает свою часть в общем цикле обработки команды. На практике нельзя обеспечить "большую длину" конвейера, при которой достигается наивысший эффект (т.к ориентация процессоров не может быть полной). Конвейерная схема нашла применение в скалярных процессорах Супер ЭВМ, в которых они применяются как специальные процессоры для поддержки векторной обработки. ПО типу конвейра работают сети, реализующие архитектуру клиент-сервер. Архитектура ОКМД предполагает создание структур векторной или матричной обработки. Системы этого типа строятся как однородные, т.е. процессорные элементы, входящие в систему, идентичны и все они управляются одной и той же последовательностью команд. Однако каждый процессор обрабатывает свой поток данных. Под эту схему хорошо подходят задачи обработки матриц или векторов (массивов), задачи решения систем, линейных и нелинейных, алгебраических и дифференциальных уравнений. Все современные супер ЭВМ комбинируют векторную и конвейерную обработку и отличаются только видами этих комбинаций. Архитектура МКМД предполагает, что все процессоры системы работают по своим программам с собственным потоком команд. Кластерные архитектуры. Круг задач, решаемых серверами, постоянно расширяется, становится многообразным и сложным. Чем выше ранг сети, тем более специализированными они становятся. В сетях первых поколений серверы строились на основе больших и очень дорогих ЭВМ (mainframe), выпускаемых целым рядом компаний: Digital Equipment, Tandem, влившихся в корпорацию Compaq, IBM, Hewlett-Packard. Все они работали под управлением ОС Unix и способны были объединяться для совместной работы. Одним из перспективных направлений является кластеризация, т.е. технология, с помощью которой несколько серверов, сами являющиеся вычислительными системами, объединяются в единую систему более высокого ранга для повышения эффективности функционирования системы в целом. Целями построения кластеров могут служить: улучшение масштабируемости (способность к наращиванию мощности); повышение надежности и готовности системы в целом; увеличение суммарной производительности; эффективное перераспределение нагрузок между компьютерами кластера; эффективное управление и контроль работы системы и т.п. Улучшение масштабируемости или способность к наращиванию мощности предусматривает, что все элементы кластера имеют аппаратную, программную и информационную совместимость. В сочетании с простым и эффективным управлением изменение оборудования в идеальном кластере должно обеспечивать соответствующее изменение значений основных характеристик, т.е. добавление новых процессоров, дисковых систем должно сопровождаться пропорциональным ростом производительности, надежности и т.п. В реальных системах эта зависимость имеет нелинейный характер. Масштабируемость SMP- и МРР-структур достаточно ограничена. При большом числе процессоров в SMP-структурах возрастает число конфликтов при обращении к общей памяти, а в МРР-структурах плохо решаются задачи преобразования и разбиения приложений на отдельные задания процессорам. В кластерах же администраторы сетей получают возможность увеличивать пропускную способность сети за счет включения в них дополнительных серверов, даже уже из числа работающих, с учетом того, что балансировка и оптимизация нагрузки будут выполняться автоматически. Следующей важной целью создания кластера является повышение надежности и готовности системы в целом. Избыточность, изначально заложенная в кластеры, способна их обеспечить. Основой этого служит возможность каждого сервера кластера работать автономно, но в любой момент он может переключиться на выполнение работ другого сервера в случае его отказа. Повышение суммарной производительности кластера, объединяющего несколько серверов, обычно не является самоцелью, а обеспечивается автоматически. Ведь каждый сервер кластера сам является достаточно мощной вычислительной системой, рассчитанной на выполнение им всех необходимых функций в части управления соответствующими сетевыми ресурсами. С развитием сетей все большее значение приобретают и распределенные вычисления. При этом многие компьютеры, в том числе и серверы, могут иметь не очень большую нагрузку. Свободные ресурсы домашних компьютеров, рабочих станций локальных вычислительных сетей, да и самих серверов можно использовать для выполнения каких-либо трудоемких вычислений. При этом стоимость создания подобных вычислительных кластеров очень мала, так как все их составные части работают в сети и только при необходимости образуют виртуальный (временный) вычислительный комплекс. Работа кластера под управлением единой операционной системы позволяет оперативно контролировать процесс вычислений и эффективно перераспределять нагрузки между компьютерами кластера. Эффективное управление и контроль работы системы подразумевает возможность работы отдельно с каждым узлом, вручную или программно отключать его для модернизации либо ремонта с последующим возвращением его в работающий кластер. Эти операции скрыты от пользователей. Кластерное ПО, интегрированное в операционные системы серверов, позволяет работать с узлами как с единым набором ресурсов (Single System Image, SSI). Схема вычислительной системы СUDESNIK. 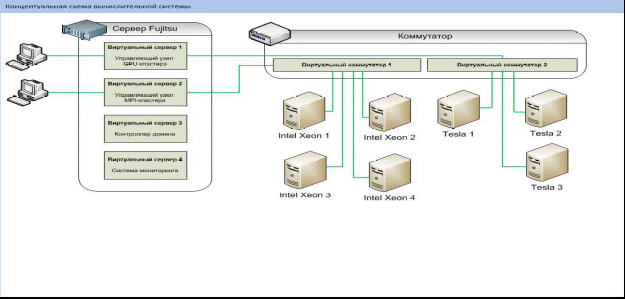 Вычислительный узел NVIDIA Tesla: Число процессоров Tesla c2070 4 Число вычислительных ядер: 1792 (448 на один процессор) Точность операций с плавающей точкой: Одинарная и двойная точность в соответствии с IEEE 754 Пиковая производительность 4,12 Тфлоп/c Объем специальной памяти: 24GB GDDR5 Интерфейс памяти: 384-bit Полоса пропускания памяти: 148 GB/sec Макс. потребление энергии: 900W TDP Системный интерфейс: PCIe x16 Gen2 Всего таких 3 вычислительных узла. Пиковая производительность всей вычислительной системы — 12,36 Тфлоп/с Установленное ПО (CudaToolkit 3.2): 1. Компиляторы CUDA C (nvcc), OpenCL (nvopencc), PTX-ассемблера (ptxas). 2. Библиотеки CUDA: CUBLAS - набор базисных подпрограмм линейной алгебры; CUFFT - быстрое преобразование Фурье; CURAND — генерация псевдо- и квазислучайные числа; CUSPARSE — разреженные матрицы. 3. Набор примеров и средств разработки (CUDA SDK) Элементы алгебры логики Алгебра логики — это раздел математической логики, значение всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями. Высказывание — это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, то есть каждое высказывание или истинно, или ложно и не может быть одновременно и истинным и ложным. Высказывания: «Сейчас идет снег» — это утверждение может быть истинным или ложным; «Вашингтон — столица США» — истинное утверждение; «Частное от деления 10 на 2 равно 3» — ложное утверждение. В алгебре логики все высказывания обозначают буквами а, Ь, с и т. д. Содержание высказываний учитывается только при введении их буквенных обозначений и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры. Простейшими операциями в алгебре логики являются операции логического сложения (иначе: операция ИЛИ, операция дизъюнкции) и логического умножения (иначе: операция И, операция конъюнкции). Для обозначения операции логического сложения используют символы + или V. а логического умножения — символы • или /\. Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий. В частности, для алгебры логики выполняются следующие законы. 1. Сочетательный: (а+b)+c = а +:(b+с), (а•b)•c = а•:(b•с). 2. Переместительный: (а + b) = (b+а), (а • b) = (b•а), 3. Распределительный: a•(b + c) = a•b + a•c, (a + b)•c = a•c+b•c. Справедливы соотношения, в частности: а + а = а а + b=b, если а<=b, а•а = а а•b=а, если а <= b, a + a•b = a a•b = b, еслиа >= b, а + b= а ,если а>=b. Наименьшим элементом алгебры логики является 0, наибольшим элементом — 1. В алгебре логики также вводится еще одна операция — отрицания (операция НЕ, инверсия), обозначаемая чертой над элементом. По определению: Справедливы, например, такие соотношения: 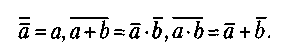 Функция в алгебре логики — алгебраическое выражение, содержащее элементы алгебры логики а, b, с, связанные между собой операциями, определенными в этой алгебре. Примеры логических функций:  Согласно теоремам разложения функций на конституанты (составляющие), любая: функция может быть разложена на конституанты 1: 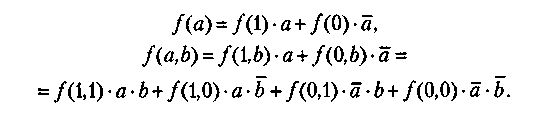 и т. д. Эти соотношения используются для синтеза логических функций и вычислительных схем. Понятие о минимизации логических функций. Проблема минимизации (упрощения) логических функций решается на основе применения законов склеивания и поглощения с последующим перебором получаемых дизъюнктивных форм и выбором из них оптимальной (минимальной). Существует большое количество методов минимизации ЛФ. Все они отличаются друг от друга спецификой применения операций склеивания и поглощения, а также различными способами сокращения переборов. Среди аналитических методов наиболее известным является метод Квайна — МакКласки, среди табличных — метод с применением диаграмм ВеЙча , Графические методы минимизации отличаются большей наглядностью и меньшей трудоемкостью, однако их применение эффективно при малом числе переменных n изменяется до 5. Машинные коды чисел. |
