Лекция на тему Понятие о симметрии в пространстве. Понятие многогранника, правильного многогранника. Призма, параллелепипед, куб. Симметрии и сечения фигур
 Скачать 438.5 Kb. Скачать 438.5 Kb.
|
|
Тема: «Понятие многогранника, правильного многогранника. Призма, параллелепипед, куб. Симметрии и сечения фигур». План: Понятие многогранника, правильного многогранника. Многогранники: параллелепипед, призма, куб. Симметрии и сечения фигур. Формулы площадей и объемов многогранников. Конспект лекции 1 Рассмотрим фигуру F 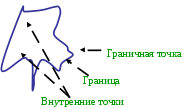 А D F В C М точка М – называется граничной точкой фигуры F, если среди сколько угодно близких к ней точек (включая её саму) есть точки, как принадлежащие фигуре, так и не принадлежащие ей. Множество всех граничных точек фигуры называется ее границей. Так, например, границей шара является сфера. Точка фигуры не является граничной, называется внутренней точкой фигуры. Каждая внутренняя точка фигуры характеризуется тем, что все достаточно близкие к ней точки пространства, также принадлежат фигуре. Так, любая точка шара, не принадлежащая сфере – его границе, является внутренней точкой шара. Фигура называется ограниченной, если ее можно заключить в какую–нибудь сферу. Очевидно что ограниченные фигуры:  шар тетраэдр параллелепипед   А прямая и плоскость – неограниченные фигуры. Фигура называется связной, если любые 2 ее точки можно соединить непрерывной линией, целиком принадлежащей данной фигуре. Примерами связных фигур является тетраэдр, параллелепипед, плоскость. Фигура, состоящая из 2х параллельных плоскостей не является связной. Геометрическим телом (или просто телом) называют ограниченную связную фигуру в пространстве, которая соединяет все свои граничные точки, причем сколько угодно близко от любой граничной точки находятся внутренние точки фигуры. Границу тела называют также его поверхностью и говорят, что поверхность ограничивает тело. Плоскость, по обе стороны от которой имеются точки данного тела, называется секущей плоскостью. Фигура, которая образуется при пересечении тела плоскостью (т.е. общая часть тела и секущей плоскости), называется сечением тела. Поверхность, состоящую из многоугольников, и ограничивающую некоторое геометрическое тело называют многогранной поверхностью или многогранником. На рисунке 1 изображены примеры многогранников:    Тетраэдр Параллелепипед Октаэдр Многоугольники, из которых составлен многогранник, называются его гранями. Гранями тетраэдра и октаэдра являются треугольники, гранями параллелепипеда – параллелограммы. Стороны граней называются ребрами, а концы ребер – вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника. Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Тетраэдр, параллелепипед, октаэдр – выпуклые многогранники. На рисунке 2 – невыпуклый многогранник.  Все грани выпуклого многогранника являются выпуклыми многоугольниками! В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и тоже число ребер. Примером правильного многоугольника является куб. Все его грани – равные квадраты, и в каждой вершине сходятся 3 ребра. Очевидно, все ребра правильного многогранника равны друг другу. Так же равны все двугранные углы, содержащие две грани с общим ребром. Не существует правильного многогранника, гранями которого является правильные 6 –ти угольники, 7-угольники и вообще n-угольники при n 6. Поэтому каждая вершина правильного многоугольника может быть вершиной либо 3х, 4х или 5ти равносторонних треугольников, либо 3х правильных 5 – угольников. Других возможностей нет. Симметрия в пространстве В планиметрии рассматриваются фигуры, симметричные относительно точки и прямой, а в стереометрии – относительно точки, прямой и плоскости. 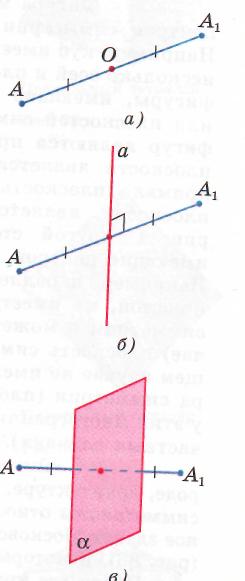   Точка (прямая, плоскость)называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость симметрии), то говорят, что она обладает центральной (осевой, зеркальной) симметрией. Фигура может иметь один или несколько центров симметрии (осей симметрии, плоскостей симметрии). Например, параллелепипед, куб. Существуют фигуры, имеющие бесконечно много центров, осей или плоскостей симметрии. Простейшими из таких фигур являются прямая и плоскость. Любая точка плоскости является её центром симметрии. Любая прямая (плоскость), перпендикулярная к данной плоскости, является её осью (плоскостью) симметрии. Существуют фигуры, не имеющие центров, осей или плоскостей симметрии. Например, тетраэдр. - 2 – Параллелепипед. Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны (рисунок 3). Четырехугольники АВВ1А1, ВСС1В, СDD1C, DАА1D1 также являются параллелограммами, т.к. каждую из них имеющую попарно параллельные противоположные стороны. 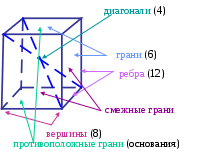 D1 C1 A1 B1 D C A B РИС. 3 Поверхность, состоящая из 2х равных параллелограммов АВСD и А1В1С1D1 и 4х параллелограммов АВВ1А1, ВСС1В, СDD1C, DАА1D1 называется параллелепипедом и обозначается АВСDА1В1С1D1 Параллелограммы, из которых составлен параллелепипед, называется гранями, их стороны – ребрами, а вершины параллелограммов - вершинами параллелепипеда. Параллелепипед имеет 6 граней, 12 ребер и 8 вершин. Две грани параллелепипеда, имеющие общее ребро называются смежными, а не имеющие общих ребер – противоположными. Две вершины, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Каждый параллелепипед имеет 4 диагонали (АС1, ВD1, CA1 и DВ1). Любые две противоположные грани – основания, а остальные грани – боковые грани параллелепипеда. Ребра параллелепипеда, не принадлежащие основаниям, называются боковыми ребрами. Свойства параллелепипеда: 1. Противоположные грани параллелепипеда параллельны и равны. 2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. (Доказать самостоятельно). Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники. Например, ящики, комнаты и т.д. Свойства прямоугольного параллелепипеда: 1. В прямоугольном параллелепипеде все 6 граней – прямоугольники Полуплоскости, в которых расположены смежные грани параллелепипеда, образуют двугранные углы, которые называются двугранными углами параллелепипеда. 2. Все двугранные углы прямоугольного параллелепипеда – прямые. Длины 3х ребер, имеющих общую вершину, называется измерениями прямоугольного параллелепипеда. Для измерения комнаты используется «длина», «ширина», «высота», а это и есть измерения. Длины смежных сторон можно назвать измерениями прямоугольника, и поэтому квадрат диагонали прямоугольника = сумме квадратов 2х его измерений. Аналогичным свойством обладает и прямоугольный параллелепипед. Теорема: Квадрат диагонали прямоугольного параллелепипеда = сумме квадратов 3х его измерений. Следствие. Диагонали прямоугольного параллелепипеда равны. Т.к. параллелепипед имеет 6 граней, то его сечениями могут быть: Треугольники и четырехугольники (рис.а), Пятиугольники (рис.б), шестиугольники(рис.в).  На рисунке показаны центр, ось и плоскость симметрии прямоугольного параллелепипеда: 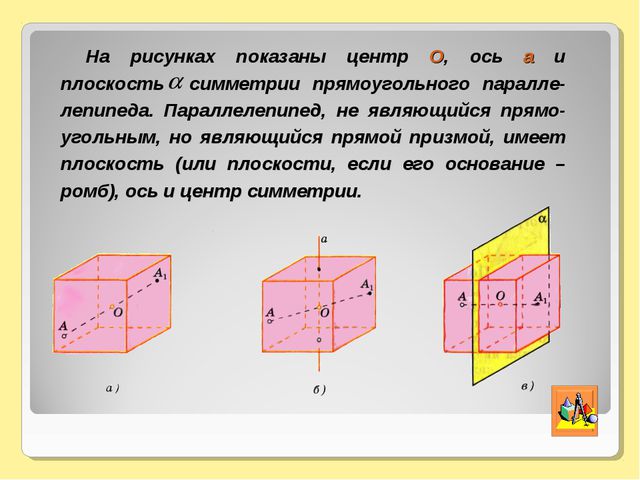 Куб Прямоугольный параллелепипед, у которого все 3 измерения равны, называется кубом. Все грани куба – равные друг другу квадраты. Куб состоит из 6 квадратов, в каждой вершине сходятся 3 квадрата, сумма плоских углов равна 270. Симметрия в кубе:  Плоскости симметрии: 3 плоскости симметрии, проходящие через середины параллельных ребер; 6 плоскостей симметрии, проходящие через противолежащие ребра. 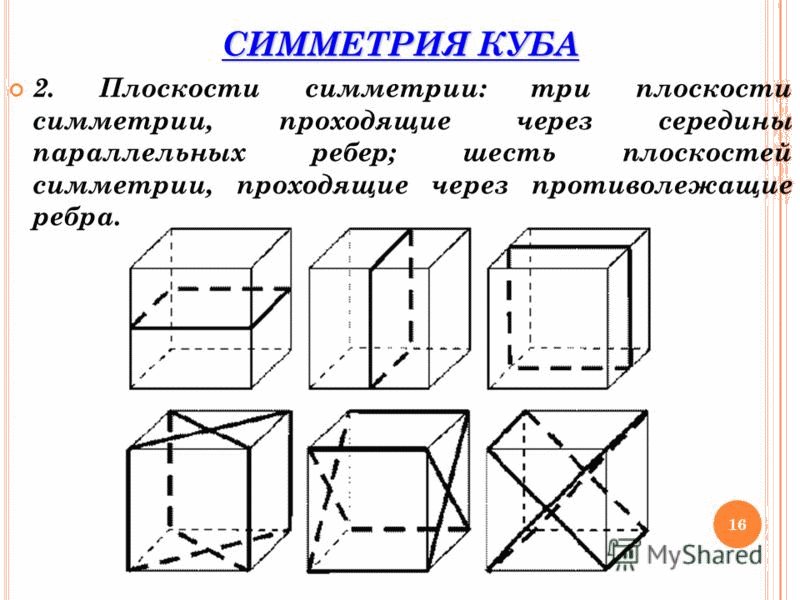 Призма. Рассмотрим 2 равных многоугольника А1А2 … Аn и В1В2 … Вn, расположенных в параллельных плоскостях и так, что отрезки А1В1, А2В2, … , АnВn соединяющие соответственные вершины многоугольников, параллельны. (рисунок 4). Каждый из n 4х угольников А1А2В2В1, А2А3В3В2, … , АnА1В1Вn является параллелограммом, т.к имеет попарно параллельные противоположные стороны. Например, в 4х угольнике А1А2В2В1 стороны А1В1 и В1В2 параллельны по условию, а стороны А1А2 и В1В2 по свойству параллельных плоскостей, пересеченных 3ей плоскостью. 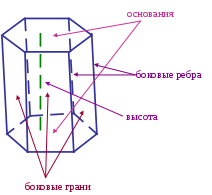 Bn Bn B1 С β B2  An A1 Н α A2 РИС. 4. Многогранник, составленный из 2х равных многоугольников А1А2 … Аn и В1В2 … Вn , расположенных в параллельных плоскостях, и n параллелограммов А1А2В2В1, А2А3В3В2, … , АnА1В1Вn , называется призмой. Многоугольники А1А2 … Аn и В1В2 … Вn – основания, а параллелограммы А1А2В2В1, А2А3В3В2, … , АnА1В1Вn – боковые грани призмы. Отрезки А1В1, А2В2, … , АnВn – боковые ребра. Эти ребра как противоположные стороны параллелограммов А1А2В2В1, А2А3В3В2, … , АnА1В1Вn, последовательно приложенных друг к другу, равны и параллельны. Призму с основаниями А1А2 … Аn и В1В2 … Вn обозначают А1А2…АnВ1В2…Вn и называют n – угольной призмой. Перпендикуляр, проведенный из любой точки одного основания к плоскости другого основания, называется высотой. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру. Прямая призма называется правильной, если её основания правильные многоугольники. У такой призмы все боковые грани равные прямоугольники. 3 Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы - сумма площадей ее боковых граней. Sполн выражается через Sбок и Sосн-я Sполн = Sбок + 2Sосн Для прямой призмы: Sбок = Р · h , где Р – периметр основания, h – высота призмы, т.к. боковые грани – прямоугольники. Для прямоугольного параллелепипеда: Sполн = Sбок + 2Sосн , Sбок = Р · h , где Р – периметр основания, h – высота Для куба: Sполн = 6 · a2 , Sбок = 4 · a2 Объемы различных тел. Теорема 1 Объем прямоугольного параллелепипеда равен произведению трех его измерений. V=abc. Следствие 1 Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. V=Sh. Следствие 2 Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. V=Sh. Теорема 2 Объем прямой призмы равен произведению площади основания на высоту. V=Sh. Заполнить таблицу. Площади поверхностей и объёмы многогранников и тел вращения
Письменно ответить на вопросы. Что называется геометрическим телом? Что называют поверхностью тела? Что называется сечением тела? Что называется многогранником? Что называется гранями многогранника? Что называется ребрами и вершинами многогранника? Что называется диагональю многогранника? Какой многогранник называется выпуклым? Какую фигуру называют параллелепипедом? В каком случае параллелепипед является прямоугольным? Чему равен квадрат диагонали прямоугольного параллелепипеда? Какая фигура называется призмой? В каком случае призма является прямой? Какой многогранник называется правильным? Какая формула выражает площадь полной поверхности призмы? Какая формула выражает площадь боковой поверхности прямой призмы? |
