САИПР КР. Контрольная_работа_Тихомиров_И_М_ИБ_05з. Понятия альтернативы, не улучшаемой альтернативы и что такое множество Парето. Геометрическое представление
 Скачать 62.87 Kb. Скачать 62.87 Kb.
|
|
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ㅤ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ㅤ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ㅤ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ㅤ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ) ИНСТИТУТ ㅤ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ Дисциплина: Системный анализ и принятие решений Контрольная работа Реферат на тему: Понятия альтернативы, не улучшаемой альтернативы и что такое множество Парето. Геометрическое представление Фамилия: Тихомиров Имя: Иван Отчество: Михайлович Группа ㅤ №: ИБ-05з № зачетн. книги: 2010580 Проверил:_____________ Санкт-Петербург 2023 Содержание Введение 3 Закон Парето 4 Множество Парето 6 Метод условной многокритериальной оптимизации 9 Заключение 12 Список используемых источников 13 Введение В начале второго тысячелетия было установлено, что при выполнении определенных двух аксиом «разумного» выбора всякое решение задачи многокритериального выбора всегда содержится в множестве Парето. Иными словами, наилучшее решение задачи многокритериальной оптимизации следует искать именно в пределах множества Парето. Исследованию различных свойств множества Парето посвящена многочисленная литература. Это множество находит широкое применение при решении различного рода прикладных экономических и технических задач, в которых необходимо учитывать не одну, а несколько целевых функций [2]. Актуальность данной темы заключается в том, что при постановке и решении большинства экономических задач, связанных с принятием решений, имеющих вариативные последствия, зачастую необходимо произвести выбор в некотором поле альтернатив, являющихся результатом уже сделанного выбора, то есть из хорошего выбрать лучшее [3]. Целью данной работы является рассмотрение теории множества Парето, а геометрическое представление методов условной многокритериальной оптимизации. Закон Парето Закон Парето, или принцип 20/80 — эмпирическое правило, получившее свое название в честь экономиста и социолога Вильфредо Парето (Vilfredo Pareto, 1848–1923), в наиболее общем виде формулируется как «20% усилий дают 80% результата, а остальные 80% усилий — лишь 20% результата». Принцип 20/80 может использоваться как базовая установка в анализе факторов эффективности какой-либо деятельности и оптимизации ее результатов: правильно выбрав минимум самых важных действий, можно быстро получить значительную часть от планируемого полного результата, при этом дальнейшие улучшения неэффективны и могут быть неоправданными (согласно кривой Парето). Следствия из закона Парето формулируются следующим образом. 1. Большая часть усилий не дает желаемых результатов. 2. То, что мы видим, не всегда соответствует действительности — всегда имеются скрытые факторы. 3. То, что мы рассчитываем получить в результате, как правило, отличается от того, что мы получаем, — всегда действуют скрытые силы. 4. Обычно слишком сложно и утомительно разбираться в том, что происходит, а часто это и не нужно: необходимо лишь знать — работает ли ваша идея, и изменять ее так, чтобы она заработала, а затем поддерживать ситуацию до тех пор, пока идея не перестанет работать. 5. Большинство удачных событий обусловлено действием небольшого числа высокопроизводительных сил; большинство неприятностей связано с действием небольшого числа высокодеструктивных сил. 6. Большая часть действий, групповых или индивидуальных, являет собой пустую трату времени. Математический анализ закона Парето позволяет высказать в его отношении две основные претензии: • в качественной формулировке (т.е. без учета конкретных значений 20/80) закон представляет собой тривиальное с позиций математики наблюдение, согласно которому в ситуации, когда результат складывается из действия множества различных факторов, вклад этих факторов в результат часто бывает различным; • количественная часть закона математически очевидно некорректна: 1) действительное распределение вклада большей и меньшей частей факторов в реальной жизни бывает каким угодно, и вовсе не обязательно оно равно 20/80; 2) легко проверить, что конкретные значения распределения меняются даже при анализе одних и тех же данных, достаточно изменить правила группировки выборочных значений; 3) можно также заметить, что основное следствие закона Парето, на котором базируется все его применение — то, что факторов, дающих наибольший вклад в результат, всегда немного, — является лишь эмпирическим наблюдением, которое вовсе не обязано сбываться в каждом конкретном случае. Указанные факты определяют границы применимости закона Парето: он ни в коем случае не должен рассматриваться как непреложный закон природы с конкретно заданными числовыми параметрами. Применение же его в качестве общего принципа, требующего обращать внимание на неравномерность вклада разных факторов в результат и необходимость уделять различное внимание разным по важности факторам, вполне оправдано и полезно. В применении принципа Парето есть еще один «подводный камень»: в реально существующих системах такие свойства как полнота, качество, функциональность описываются не одним параметром, а некоторой их совокупностью. Даже если распределение вклада различных факторов в каждый из этих параметров по отдельности определяется законом Парето, как правило, вклады одного и того же фактора в различные параметры системы неодинаковы. Один и тот же фактор для одного параметра может относиться к числу малозначительных, для другого — попасть в число определяющих. Поэтому, пытаясь оптимизировать что-либо путем избавления от ненужных частей, оптимизатор должен быть уверен, что учитывает все существенные параметры системы. Несмотря на критику, закон, описанный Парето, и выявленные им статистические закономерности используются в методах оптимизации, включая методы выбора оптимальных альтернатив [1]. Множество Парето Множеством Парето называется множество, безусловно, несравнимых альтернатив, оставшихся после отбрасывания всех безусловно худших альтернатив. Как отмечается в [3], «…далеко не всегда возможно представить задачи поиска наиболее подходящего варианта действий в классической математической форме решения задачи оптимизации, т.е. максимизации или же минимизации целевой функции (единственного критерия выбора). В связи с этим возникли и получили широкое распространение многокритериальные постановки задачи выбора решения, основанные на явном признании наличия нескольких частных критериев выбора». А не очевидность преимуществ рождает необходимость введения дополнительного критерия оценки, что, в свою очередь, может сделать возможным применение подхода, именуемого оптимизацией по Эджворту – Парето и состоящего в следующем: некоторый возможный (допустимый) вариант действий является оптимальным по Парето, если при замене его любым другим допустимым вариантом нельзя добиться улучшения значения хотя бы одного из критериев, не ухудшив при этом какого-то другого [3]. Оптимальность по Парето — такое состояние системы, при котором значение каждого частного показателя (критерия), характеризующего систему (принятия решений), не может быть улучшено без ухудшения других. Таким образом, по словам самого Парето: «Всякое изменение, которое никому не приносит убытков, а некоторым приносит пользу (по их собственной оценке), является улучшением». Значит, признается право на все изменения, которые не приносят никому дополнительного вреда и оптимальным решением принимается такое, которое является доминирующим. Определение: альтернатива А называется доминирующей по отношению к альтернативе В, если по всем критериям оценки альтернативы А не хуже, чем альтернативы В, а хотя бы по одному критерию оценка А лучше. Альтернатива В при этом называется доминируемой [1]. 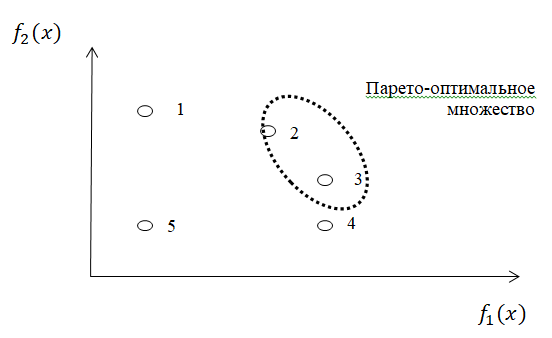 Рис. 1 Парето-оптимальное множество 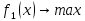 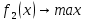 Отношение Парето: (yi, yj) ∈ Rp → ∀k: [ fk(yi) ≥ fk(yj)] ∧ [ f(yi) ≠ f(yj)]. 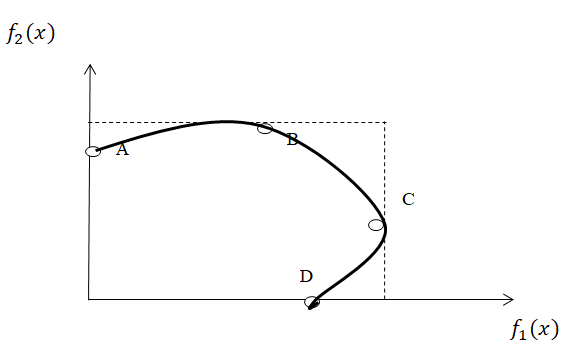 Рис. 2 – Отношение Парето Если для некоторой точки  Y не существует более предпочтительной по Парето точки, т.е. такой точки y, что (y, Y не существует более предпочтительной по Парето точки, т.е. такой точки y, что (y,  ) )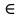 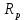 , то тогда точка , то тогда точка  называется эффективным, или парето-оптимальным решением многокритериальной задачи, относится к множеству Парето (рис. 1). называется эффективным, или парето-оптимальным решением многокритериальной задачи, относится к множеству Парето (рис. 1).Aльтернатива является парето-оптимальной, если она лучше других по какому-то из критериев. Альтернативы, принадлежащие к множеству Парето, называются несравнимыми. Их невозможно сравнить непосредственно на основе критериальных оценок. Они не находятся в отношении доминирования. Далее приводятся аксиомы, являющиеся основой принципа Парето. • Аксиома исключения доминирующих решений: для всякой пары допустимых решений x′, x′′ 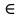 X, для которых имеет место соотношение x′ X, для которых имеет место соотношение x′ 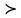 X x′′, выполнено x′′ X x′′, выполнено x′′ 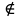 C(X). C(X).• Аксиома Парето: для всех пар допустимых решений x′, x′′ 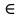 X, для которых имеет место неравенство f(x′) ≥ f(x′′), выполняется соотношение x′ X, для которых имеет место неравенство f(x′) ≥ f(x′′), выполняется соотношение x′ 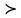 X x′′, X x′′,где 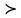 X — отношение предпочтения; X — отношение предпочтения;X — множество допустимых решений; f — векторный критерий. Принцип Парето: наилучшее решение многокритериальной задачи всегда выбирается из парето-оптимального множества. Алгоритм нахождения множества Парето: 1. Принять P(Y) = Y, i = 1, j = 2. Создается текущее множество парето-оптимальных векторов, которое в начале совпадает с множеством Y. 2. Проверить выполнение неравенства y (i) ≥ y ( j). Если да, то перейти к п. 3. Если нет, то перейти к п. 5. 3. Удалить из текущего множества P(Y) вектор y(i), так как он не является парето-оптимальным. Перейти к п. 4. 4. Проверить выполнение неравенства j < N. Если да, то положить j = j + 1 и вернуться к п. 2. Если нет, то перейти к п. 7. 5. Проверить выполнение неравенства y(i) ≥ y( j). Если да, то перейти к п. 6. Если нет, то перейти к п. 4. 6. Удалить из текущего множества P(Y) вектор y(i), так как он не является парето-оптимальным. Перейти к п. 7. 7. Проверить выполнение неравенства i < N − 1. Если да, то положить i = i + 1, j = j + 1 и вернуться к п. 2. Если нет, закончить вычисления. Таким образом, рассмотрев наиболее распространенные подходы к поиску оптимального решения многокритериальных задач, в том числе в условиях неопределенности, на практике именно метод парето-оптимальности будет наиболее удобным и эффективным, поскольку позволяет выделить ряд критериев, не вносящих существенный вклад в достижение оптимальной эффективности и выбрать оптимального решение[1]. Описанный закон Парето лежит в основе метода достижимых целей (МДЦ). Метод условной многокритериальной оптимизации Парето-оптимизация позволяет найти такое состояние системы, при котором значение каждого частного показателя (критерия), характеризующего систему (принятия решений), не может быть улучшено без ухудшения других. Данный метод оперирует таким понятием как недоминируемые цели (или альтернативы). Дадим краткое толкование недоминируемой цели: альтернатива А называется доминирующей (или недоминируемой) по отношению к альтернативе В, если по всем критериям оценки альтернативы А не хуже, чем альтернативы В, а хотя бы по одному критерию оценка А лучше. Альтернатива В при этом называется доминируемой (или недоминирующей). Другими словами, при прочих одинаковых условиях альтернатива А лучше альтернативы В. Данный метод также основывается на том, что оптимизировать можно лишь небольшую часть критериев, остальные же надо либо зафиксировать, либо наложить некие ограничения. Это основано на том, что среди всего множества критериев лишь небольшая часть вносит существенный вклад в качественные признаки системы соответственно одновременно оценивать все множество критериев затруднительно и бессмысленно с позиции закона Парето (20% критериев составляют 80% от всей оценки системы). Итак, данный метод предполагает следующие шаги: построение множества достижимых целей (альтернатив) в пространстве критериев (выбранных для оптимизации); создание графиков, визуально отображающих кривые объективного замещения между различными парами критериев; выбор оптимальной (компромиссной) цели; расчет выбранной цели и выработка стратегии по внедрению выбранной системы [1]. Рассмотрим данный метод более подробно на примере. Пусть существуют четыре альтернативных друг другу проекта; обозначим их через x1, x2, x3, x4, причем xi > 0 (i = 1...4), Σxi = 1. Пусть существует три критерия, которые мы выбрали для оценки, остальные были приняты как константы (или были наложены ограничения). 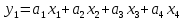 — критерий общей стоимости системы, — критерий общей стоимости системы,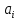 — стоимость i-альтернативы. — стоимость i-альтернативы. — критерий риска, оставшегося после внедрения системы, — критерий риска, оставшегося после внедрения системы, Где  — риск до внедрения системы; — риск до внедрения системы; 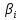 — остаточный риск i-й альтернативы; — остаточный риск i-й альтернативы; 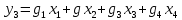 — критерий надежности. — критерий надежности. Рассмотрим альтернативы, оценив их по критериям 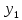 и и 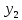 . Пусть заданы такие значения коэффициентов, что в результате получается следующий график (рис. 3). . Пусть заданы такие значения коэффициентов, что в результате получается следующий график (рис. 3).Поскольку оба параметра необходимо уменьшить (стоимость и риски), то юго-западная граница области содержит подмножество парето-оптимальных решений. К этой области принадлежит одна единственная точка с координатами (2, 1). Она является парето-оптимальной, потому что при одном и том же уровне риска ее стоимость меньше чем у точки (4, 1), иначе говоря, увеличение стоимости после точки (2, 1) не приводит к значительному снижению рисков, значит решение (4, 1) неоптимально [1].  Рис. 3 – Кривая объективного замещения стоимости и остаточных рисков Метод достижимых целей позволяет создавать огромное множество парных критериальных графиков, однако для каждого такого графика будет иметься своя область эджварто-парето (ОЭП или недоминируемое множество), при чем эти множества для каждой пары критериев не обязательно должны пересекаться. Потому если необходимо найти решения оптимальные сразу по не сколь ким показателям (трем и более), то надо располагать альтернативы в трехмерном (n-мерном) пространстве отобранных критериев. Однако анализировать трехмерные пространства с целью поиска областей оптимальных решений трудно, поэтому предлагается использовать серию рисунков из двумерных сечений трехмерной фигуры, содержащих множество допустимых решений. Анализ двумерных сечений аналогичен анализу альтернатив в плоскости. При числе критериев более трех на оставшиеся необходимо накладывать ограничения, использовать методы свертки и сечений многомерных пространств. Так, например, при одновременной оптимизации четырех критериев получается четырехмерное пространство (пространственно-временной континуум — длина, ширина, высота и время). Оно может быть представлено в виде одномерного массива времени, элементы которого содержат трехмерное пространство на конкретный момент времени, которое, в свою очередь, сворачивается при помощи наборов двумерных сечений. Визуально это можно отобразить при помощи анимации, видео или переключателя кадров, где каждый кадр — набор сечений в данный момент времени (под словами длина, ширина, высота, время понимаем критерии, выбранные для оптимизации); таким образом, беря значение четвертого критерия за константу, можно отобразить двумерное сечение для этой константы. В случае пяти критериев можно представить их как двумерный массив сечений, или как одномерный массив пятого критерия, элементами которого является одномерный массив четвертого критерия (время), который содержит наборы двумерных сечений (двумерное представление трехмерного объекта). В этом случае надо закреплять уже два параметра (четвертый и пятый критерии) и вычислять для этих констант двумерные сечения. Задача выбора альтернативных проектов построения систем в пространстве трудно формализуемая, многокритериальная и происходит в условиях частичной неопределенности (не все альтернативы и критерии заданы и описаны изначально), а значит, не поддается четкой алгоритмизации. Поэтому система поддержки принятия решений должна только делать расчеты для выбранных решений, формировать множества оптимальных решений и отображать их графически, а не принимать решение о выборе конкретной оптимальной альтернативы из построенного множества. Само принятие решения должно остаться за человеком — специалистом в области защиты информации, который, руководствуясь собственным опытом, знаниями и интуицией, сможет выбрать верное решение. Поэтому главная задача системы поддержки принятия парето-оптимальных решений в области проектирования— помочь лицам, принимающим решения принять оптимальное (компромиссное) решение в заданных условиях, причем достаточно оперативно и наглядно, а также обосновано. Заключение Множеством Парето называется множество, безусловно, несравнимых альтернатив, оставшихся после отбрасывания всех, безусловно, худших альтернатив. Оптимальность по Парето — такое состояние системы, при котором значение каждого частного показателя (критерия), характеризующего систему (принятия решений), не может быть улучшено без ухудшения других. Таким образом, по словам самого Парето: «Всякое изменение, которое никому не приносит убытков, а некоторым приносит пользу (по их собственной оценке), является улучшением». Значит, признается право на все изменения, которые не приносят никому дополнительного вреда и оптимальным решением принимается такое, которое является доминирующим. Рассмотрев наиболее распространенные подходы к поиску оптимального решения многокритериальных задач, в том числе в условиях неопределенности, на практике именно метод парето-оптимальности будет наиболее удобным и эффективным, поскольку позволяет выделить ряд критериев, не вносящих существенный вклад в достижение оптимальной эффективности и выбрать оптимального решение[1]. Задача выбора альтернативных проектов построения систем в пространстве трудно формализуемая, многокритериальная и происходит в условиях частичной неопределенности (не все альтернативы и критерии заданы и описаны изначально), а значит, не поддается четкой алгоритмизации. Поэтому система поддержки принятия решений должна только делать расчеты для выбранных решений, формировать множества оптимальных решений и отображать их графически, а не принимать решение о выборе конкретной оптимальной альтернативы из построенного множества. Само принятие решения должно остаться за человеком — специалистом в области защиты информации, который, руководствуясь собственным опытом, знаниями и интуицией, сможет выбрать верное решение. Поэтому главная задача системы поддержки принятия парето-оптимальных решений в области проектирования— помочь лицам, принимающим решения принять оптимальное (компромиссное) решение в заданных условиях, причем достаточно оперативно и наглядно, а также обосновано. Список используемых источников Баранова Е. К. Моделирование системы защиты информации: Практикум: Учебное пособие / Е.К.Баранова, А.В.Бабаш// М.: ИЦ РИОР: НИЦ ИНФРА-М, 2015 - 120 с. Ногин В.Д. Расслоение конечного множества Парето/ Ногин В.Д.// Актуальные проблемы гуманитарных и естественных наук. 2015. № 12-1. С. 28-30. Часовников С.Н. Портфель финансовых инструментов: оптимальность по Эджворту – Парето/ Часовников С.Н., Кирьянов И.В.// Сибирская финансовая школа. 2012. № 3 (92). С. 84-90. |
