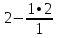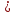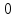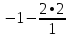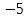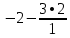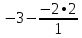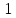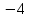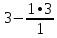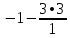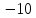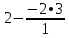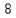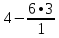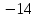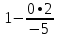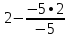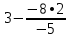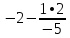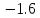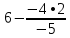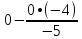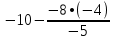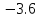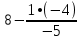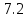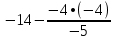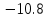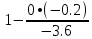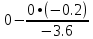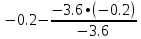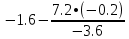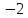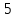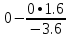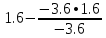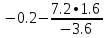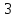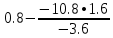фыв. Последовательно будем выбирать разрешающий элемент рэ, который лежит на главной диагонали матрицы

• Название: Последовательно будем выбирать разрешающий элемент рэ, который лежит на главной диагонали матрицы
• Дата: 06.07.2022
• Размер: 11.14 Kb.
• Имя файла: 249595889.docx
• Тип: Документы; #626139

Запишем систему в виде: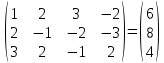



Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.

Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.

НЭ = СЭ - (А∙В)/РЭ

РЭ - разрешающий элемент (1), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.

Представим расчет каждого элемента в виде таблицы:

x1	x2	x3	x4	B
1 / 1 = 1	2 / 1 = 2	3 / 1 = 3	-2 / 1 = -2	6 / 1 = 6

В итоге получаем:



Разрешающий элемент равен (-5). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

Представим расчет каждого элемента в виде таблицы:

x1	x2	x3	x4	B
0 / -5 = 0	-5 / -5 = 1	-8 / -5 = 1.6	1 / -5 = -0.2	-4 / -5 = 0.8

В итоге получаем: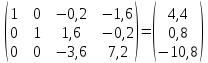



Разрешающий элемент равен (-3.6). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

Представим расчет каждого элемента в виде таблицы:

x1	x2	x3	x4	B
0 / -3.6 = 0	0 / -3.6 = 0	-3.6 / -3.6 = 1	7.2 / -3.6 = -2	-10.8 / -3.6 = 3

В итоге получаем: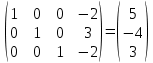



x₁=5

x₂=-4

x₃=3

Теперь исходную систему можно записать так (общее решение):

x₁ = 5 + 2x₄

x₂ = -4 - 3x₄

x₃ = 3 + 2x₄

Базисное решение получаем приравниванием переменной x₄ к нулю.

x₁ = 5

x₂ = -4

x₃ = 3

Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное. Для получения опорного решения, необходимо подобрать такие переменной x₄, при которых базисные переменные будут больше или равны нулю.
Решение было получено и оформлено с помощью сервиса:

Базисные решения системы линейных уравнений методом Жордана-Гаусса

источник:

Метод Гаусса и метод Жордано-Гаусса

Вместе с этой задачей решают также:

Метод Гаусса

Правило прямоугольника

Каноническая форма ЗЛП

Координаты вектора в базисе

Решения СЛАУ методом простой итерации

Решения СЛАУ методом простой Зейделя

Умножение матриц онлайн

По координатам пирамиды найти: уравнение плоскостей, уравнение прямых