лаба. Построение алгоритмов и проведение расчетов

• Название: Построение алгоритмов и проведение расчетов
• Дата: 14.03.2023
• Размер: 191 Kb.
• Имя файла: 1_Osnovy_programmirovania_v_srede_Scilab.doc
• Тип: Документы; #989282

1. Построение алгоритмов и проведение расчетов

1. Описание основных панелей визуального интерфейса среды Scilab

Основные панели интерфейса включают:

1. 
   Командное окно Scilab служит для ввода команд и вывода результатов. Базовый синтаксис задания (определения) любых переменных: переменная A = переменная B. Например, для задания числа в рабочем окне команд необходимо ввести: >> A=2. и нажать клавишу «Enter». Результатом выполнения команды будет присвоение переменной A значения 2. Для вывода значения необходимо набрать в командном окне имя переменной:
   

>> A

A = 2

Если в вводимой команде не указан знак равенства, то результат выполнения команды присвоиться универсальной переменной ans, например:

>> 2+3

ans = 5

2. 
   Обозреватель переменных содержит все определенные переменные, их наименование и значение. Двойной клик на переменной в обозревателе открывает таблицу для просмотра ее значения.
   
3. 
   Обозреватель файлов представляет все файлы, находящиеся в текущей (рабочей) папке. Путь к рабочей папке отображается под позицией вкладок интерфейса вместе с обозревателем для выбора текущей рабочей папки и списком рабочих папок, используемых ранее.
   

2. Реализация алгоритмов в скриптах.

Расчетные алгоритмы нужно реализовывать в специализированных файлах-скриптах среды Scaliab, имеющих расширение *.sci. Скрипт представляет собой текстовый файл в котором команды записаны одна за другой. При запуске скрипта происходит последовательное выполнение всех команд.
Редактирование скрипта может осуществляться в любом текстовом редакторе, в среде Satlab для этого используется специальный редактор SciNotes – его можно вызвать через меню «Инструменты»/ Запуск скрипта в редакторе осуществляется при нажатии F5 или кнопки RUN в панели меню редактора. Отдельные команды можно выделить и исполнить нажатием сочетаний клавишей CTRL+E.

Комментирование команд в редакторе осуществляется сочетанием клавиш CTRL+D, снятие комментариев - CTRL+SHIFT+D. Новые комментарии вставляются после символов //
При любом (пере)объявлении переменной в программе, эта переменная и ее значение хранится в памяти (отображается в списке переменных). Для обеспечения корректности счета при каждом новом запуске программы рекомендуется в начале кода программы вставить команду clear, которая удаляет все переменные из памяти системы. Команда clc очистит коммандное окно. Команда close(winsid()) закроет все графические окна.

3. Задание данных

Массивы. Числовые данные в среде Scilab представляются в виде массивов. Наиболее часто используются двумерные массивы (иначе – матрицы, таблицы), размерность которых задается в виде i, j, гдеi– количество строк,аj – количество столбцов. Массивы задаются в виде последовательности элементов массива, заключенных в квадратные скобки. Примеры задания массивов:

	Одно число	Вектор-строка	Вектор-столбец	Матрица
Размерность массива	1,1	1,3	3,1	3,3
Операция	a=1	A=[1,2,3]	B=[1;2;3]	C=[1,2,3;4,5,6;7,8,9]
Результат	a=1	A=1 2 3	B= 1 2 3	C= 1 2 3 4 5 6 7 8 9

Для определения размерности массива используется функция size(имя массива), например:

size(C)

ans = 3 3

Для получения количества строк используется операция size(имя массива,1), количества столбцов – size(имя массива, 2).
Элементы массивов. Обращение к элементу массива осуществляется через индексы. Для двумерных массивов первый индекс задает номер строки, второй – номер столбца. Индексное обращение позволяет оперировать с векторами и массивами внутри массивов.

Пусть, например, задана матрица C, размерностью 3 на 3.

Обращение к элементу массив, расположенному в 1-й строке и 1-м столбце:

C(1,1)

ans = 1

Вывод вектора-строки из двух элементов, расположенного в 2-й строке и 2-м, 3-м столбцах матрицы C:

C(2,2:3)

ans = 5 6

Вывод вектора-столбца из трех расположенного в 2-м столбце матрицы С элементов, т.е. 2-й столбец матрицы полностью:

C(1:3,2)

ans =

2

5

8

Вывод матрицы 2 на 2, представляющей собой 1-й минор матрицы С:

C(1:2,1:2)

ans = 1 2

4 5

Обращение к 1-й строке матрицы С целиком:

>> C(1,:)

ans = 1 2 3

Обращение к матрице С целиком:

C(:,:)

ans = 1 2 3

4 5 6

7 8 9

Индексное обращение позволяет задавать отдельные элементы массивов, например, для замены в матрице B=[1,2,3;4,5,6] 1-го и 2-го элементов 2-го столбца матрицы используется обращение к этим элементам и присвоение им новых значений через вектор:

B(1:2,2)=[10;11];

B = 1 10 3

4 11 6

Аналогично для замены 2-го и 3-го элемента 2-й строки матрицы:

B(2,2:3)=[10,11];

B = 1 2 3

4 10 11
Операции с матрицами. Операции с матрицами соответствуют операциям, принятым в матричном исчислении. При операциях с матрицами необходимо корректно учитывать их размерность. Примеры различных операций:

	Умножение матрицы на число (скаляр)	Умножение вектора-строки на вектор-столбец	Умножение вектора-столбца на вектор-строку
Операция	C*2	A*B	B*A
Результат	ans = 2 4 6 8 10 12 14 16 18	ans = 14	ans = 1 2 3 2 4 6 3 6 9

Примеры операций по нахождению характеристик матриц:

Задание матрицы	Определитель матрицы	Ранг матрицы	Транспонирование матрицы
A	det(A)	rank(A)	C'
A=[1 2 3; 3 4 2; 0 2 5]	ans = 4	ans = 3	ans = 1 3 0 2 4 2 3 2 5

Обращение матрицы	Собственные числа матрицы
inv(C)	spec(A)
ans = 4 -1 -2 -3.75 1.25 1.75 1.5 -0.5 -0.5	ans = 0.2401514 + 0.i 2.2045734 + 0.i 7.5552752 + 0.i

Для начальной инициализации матриц можно использовать задание матриц нужной размерности, заполненных нулями с помощью функции zeros(). Например, задание матрицы размерности 2,2 нулями:

A=zeros(2,2)

A = 0 0

0 0
Задание последовательности значений. Под последовательностью будем понимать набор чисел x(k), где k - порядковый номер числа в последовательности, количество чисел равно k_m. Эту последовательность можно представить в виде вектора-строки размерности 1,k_m

Задание последовательности возможно следующим образом:

1) Путем прямого задания элементов последовательности в вектор-строку.

Например, последовательность {1, 2, 3, 4} задается так:

x=[1 2 3 4]

x = 1 2 3 4

2) Путем задания последовательности c помощью следующей конструкции:

x = x_min:∆x:x_max

где x_min – левый предел последовательности,

∆x– шаг изменения последовательности,

x_max – правый предел последовательности.

Количество элементов в последовательности при этом определяется автоматически. Например:

>> x=-1:0.5:1

x = -1.0000 -0.5000 0 0.5000 1.0000

3) С использованием функции для линейного распределения:

linspace(x_min, x_max, k_m)

где k_m – количество элементов в последовательности. Шаг последовательности при этом определяется автоматически. Например:

x=linspace(-1,1,5)

x = -1.0000 -0.5000 0 0.5000 1.0000

4. Проведение расчетов

Задание функциональных зависимостей. Для расчета функциональной зависимости вида y(x) = f(x) необходимо, задать последовательность значений переменной x и рассчитать последовательность значений функции y(x) одним из двух способов:

1) Прямое задание функции в виде уравнения с учетом размерности переменных и правил матричных операций.

Например, для расчета функциональной зависимости y(x) = x², определяется последовательность для значений аргумента x:

>> x=0:0.5:2

x = 0 0.5000 1.0000 1.5000 2.0000

Затем задается функциональную зависимость в виде:

>> y=x.^2

y = 0 0.2500 1.0000 2.2500 4.0000

При этом создается вектор значений функции yтой же размерности, что и у вектора переменной x.

Для того, чтобы операция возведения в квадрат в указанном примере производилась не над вектором x целиком (что невозможно) а над элементами вектора x, необходимо перед знаком операнда возведения в степень поставить точку (.^). Аналогично - для операций умножения (.*) и деления (./).

2) Расчет значений функции через цикл.

В цикле будут перебираться индексы векторов переменной и значений функции – , где определяется как кол-во элементов в векторах (с помощью команды size).

На каждом шаге цикла в соответствующий элемент вектора функции y(k) будет записываться значение функции, посчитанной для элемента вектора переменной x(k). Конструкция цикла:

for (идентификатор начала цикла) [переменная цикла = поcледовательность перебора значений переменной цикла]

[тело цикла]

end (идентификатор конца цикла)

Пример задания функции в цикле:

>> x=0:0.5:2

>> km=size(x,2)

>> for k=1:km

y(k)=x(k)^2

end
Решение систем алгебраических уравнений. Системой линейных алгебраических уравнений в общем случае называется система вида:



Общепринята матрично – векторная форма записи системы в виде:



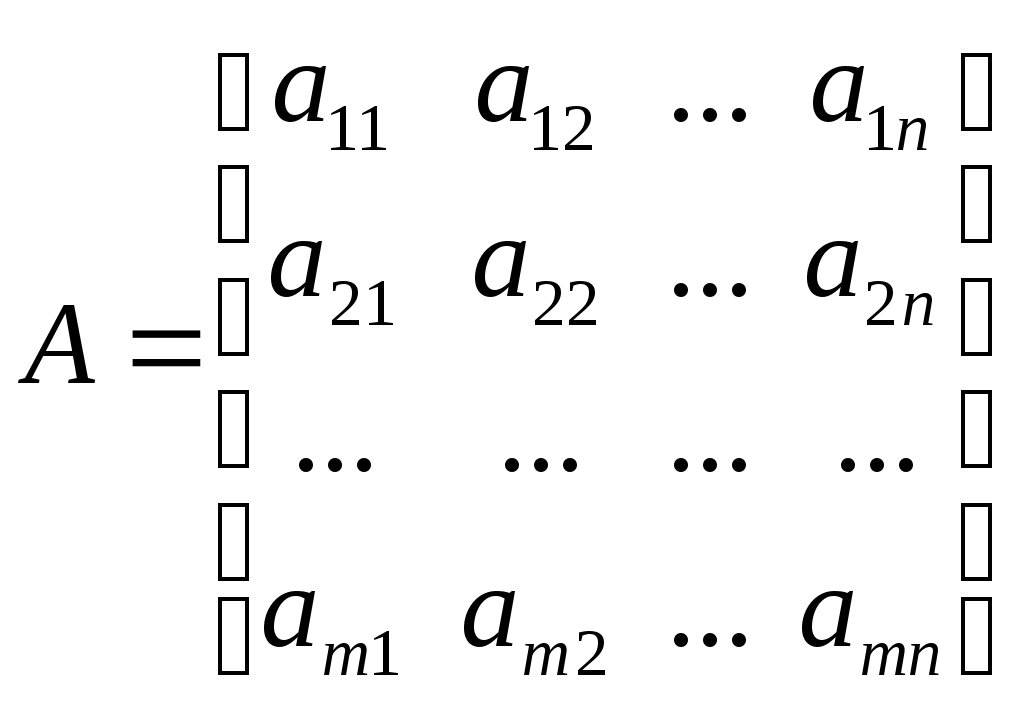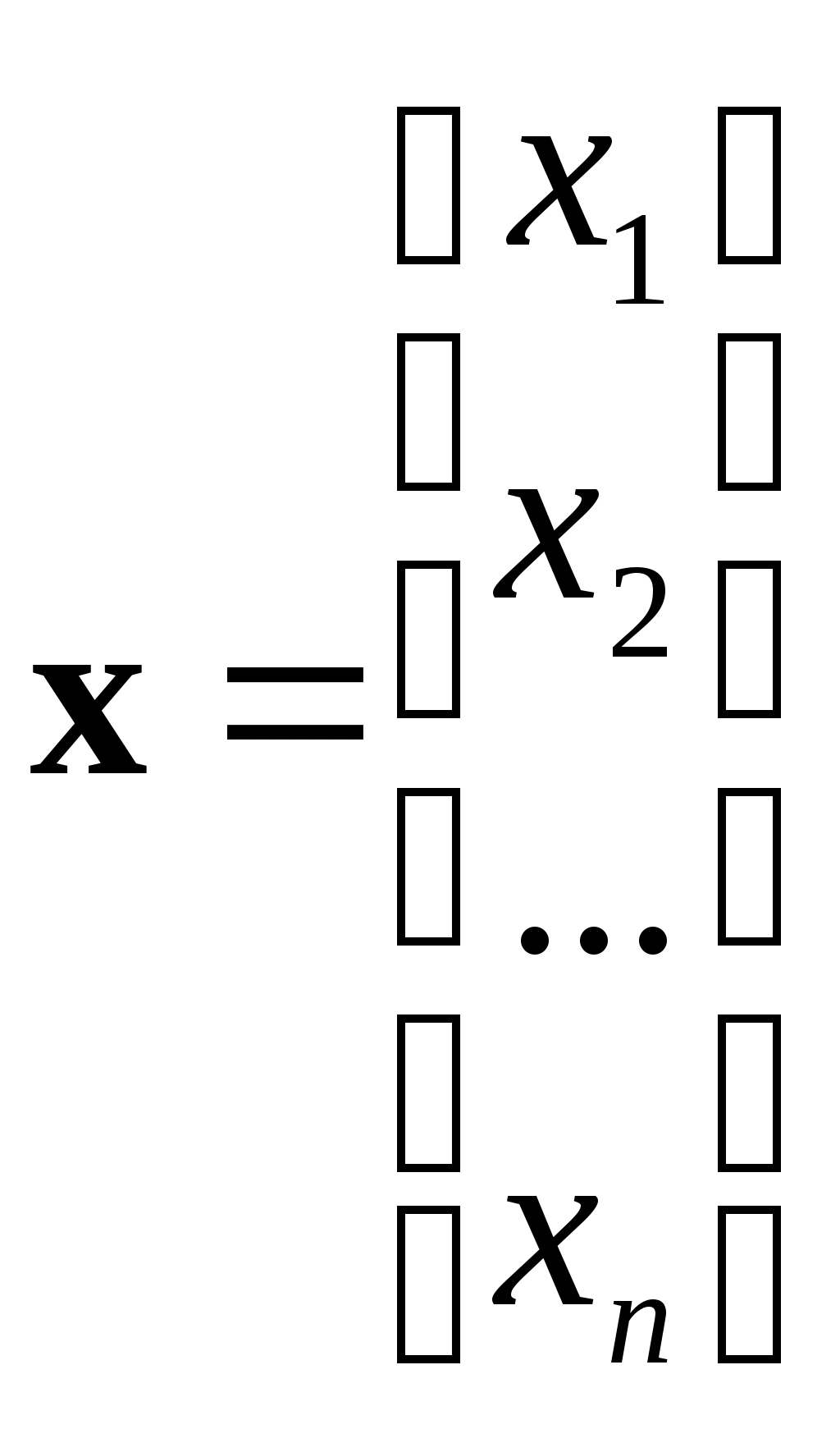где – матрица параметров левой части системы, – вектор переменных, – вектор параметров правой части системы.

Частным случаем является система, для которой , т.е. матрица является квадратной.

Для решения систем алгебраических уравнений их первоначально представляют в матричном виде – задаются матрицы и вектор , а затем находится решение при помощи операции: . Пример решения:

Операция	A=[1,3,5;3,2,6;4,5,7]	b=[22;25;35]	x=A\b
Результат	A= 1 3 5 3 2 6 4 5 7	b = 22 25 35	x = 1 2 3

5. Построение графиков

Построение графиков линий. Основным инструментом построения графиков линий является функция (в базовом виде):

plot(x,y)

где x – вектор значений по оси OX, y – вектор значений по оси OY (размерность этих векторов должна совпадать). Для обеспечения равенства размерности векторов x и y, подаваемых на вход функции plot(x,y), можно явным образом указывать диапазон перебора индексов этих векторов:

k=1:km

plot(x(k,1),y(k,1))
В результате вызова функции plot будет создано графическое окно с осями и линией графика:



Последовательное задание команд plot позволяет строить несколько графиков в одном окне
Задание атрибутов (свойств) линий. Функция plot() может задаваться с дополнительными атрибутами, представляющими расширенные возможности для построения графиков.

Сокращенный набор основных атрибутов задается в функции plot() после аргументов x и y в одинарных кавычках и имеет три составляющие:

• 
  цвет линии: 'k' – черный, 'r' – красный, 'b' – синий, 'g' – зеленый и т.д.;
  
• 
  тип линии: '-' – сплошная линия, '--' – пунктирная линия, '-.' – штрих-пунктирная линия, ':' – линия, состоящая из точек;
  
• 
  тип маркеров (отметок точек на которых построен график): 'o', '*', '+' и т.д.
  

Значения данных атрибутов можно найти в справке (Scilab Help >> Graphics > 2d_plot > LineSpec)
Для изменения любых атрибутов линий в команде plot, задается название атрибута и его значение по правилу:

plot(x,y,'Имя атрибута №1', Значение атрибута №1,'Имя атрибута №2', 'Значение атрибута №2', ...)

где 'Имя атрибута №1' задает атрибут, а Значение атрибута №1 – его значение. В зависимости от типа атрибута, его значение может быть одним числом, массивом чисел, текстовым и т.д. Если значение атрибута является текстом, то оно должно быть заключено в одинарные кавычки ' '. Пример некоторых свойств графиков:

Тип атрибута	Имя атрибута	Значение атрибута (пример)
Цвет линии	'color'	'red', 'blue' и т.д. или color(R,G,B) (R,G,B – числа от 0 до 255 – степень насыщенности красным, зеленым, синим)
Толщина линии	'LineWidth'	2
Размер отметок точек	'MarkerSize'	10
Цвет границы отметок точек	'MarkerEdgeColor'	такое же как у атрибута 'color'
Цвет заливки отметок точек	'MarkerFaceColor'	такое же как у атрибута 'color'

Полный набор значений атрибутов линий можно найти в справке по свойствам графических объектов (Scilab Help >> Graphics > GlobalProperty)

Для добавления легенды к графикам используется функция:

legend('имя 1,'имя 2', ...)

где 'имя 1,'имя 2' – имена графиков в легенде. Порядок имен должен соответствовать порядку графиков.

Для добавления подписей к осям используются функции

xlabel('подпись к оси х')

ylabel('подпись к оси y')
Пример программы с использованием расширенных возможностей при построении графиков:

plot(x,y1,'g--*','linewidth',2)

plot(x,y2,'color',color(255,100,10))

legend('y1','y2')

xlabel('x')

ylabel('x')

Результат построения:



Задание атрибутов (свойств) осей. По-умолчанию, после задания первого графика создается новое окно. Все последующие графики отображаются в этом окне. Для создания нового окна используется функция:

figure()

Также, по-умолчанию, в каждом окне создаются оси (ось X и ось Y). Для задания атрибутов осей необходимо использовать идентификатор текущих графических осей (gca), например:

a=gca()
Значения атрибутов определяются через объявленную родительскую структуру через точку. Например, значения пределов по осям заданы атрибутом data_bounds – матрица из 4-х чисел (min x, min y; max x, max y). По-умолчанию включена функция авто-подстройки пределов по осям. Для точного выставления пределов по осям необходимо задать атрибут tight_limits.

Пример задания пределов по осям

a=gca()

a.tight_limits="on"

a.data_bounds=[1.5 -14;8,67]

Результат построения:

Задания к лабораторной работе

Задание 1 (вектора и матрицы)

Составить алгоритм, выполняющий следующие операции:

• 
  задание матрицы определенной размерности;
  
• 
  определение количества строк и столбцов в матрице;
  
• 
  последовательный вывод всех элементов матрицы;
  
• 
  вывод заданной строки или столбца;
  
• 
  вывод подматрицы заданной размерности;
  
• 
  замена элементов подматрицы случайными числами;
  
• 
  замена строки или столбца матрицы значениями, полученными путем сложения остальных строк/столбцов этой же матрицы;
  
• 
  задание симметричной матрицы;
  
• 
  сложение строки или столбца данной матрицы с транспонированным столбцом/строкой этой же матрицы.
  

Задание 2 (последовательности и функции)

Составить алгоритм, выполняющий следующие операции:

• 
  задание линейной последовательности чисел x = x_min : ∆x: x_max;
  
• 
  задание аналогичной последовательности с помощью команды linspace();
  
• 
  расчет разности двух последовательностей;
  
• 
  определение среднего арифметического данной разности (должна быть близка к 0 если последовательности совпадают – проверить это);
  
• 
  задание функциональной зависимости в виде:
  

где - коэффициенты полинома (задаются вектором), - степень полинома. Значения функции должны рассчитываться двумя способами – напрямую через вектор x и через цикл;

• 
  задание функциональной последовательности в виде:
  

.

Значения функции должны рассчитываться двумя способами – напрямую через вектор x и через цикл;
Задание 3 (графики)

Построить графики 2-х произвольных функций для произвольного диапазона x. Графики отобразить на одном окне, с разными цветами, типом и толщиной линии. Добавить подписи по осям (разного шрифта, размера и цвета) и легенду. Максимум по оси OY задается как максимум из значений двух функций, минимум по оси OY - как минимум из значений двух функций.

Реализовать программу в которой каждый из графиков будет отображаться в отдельном окне, диапазоны по осям OX и OY будут задаваться как максимумы и минимумы векторов аргументов функции и ее значений.