ЛИН.+АПГЕБРА+СО. Лекция Ранг матрицы Пусть имеется некоторая матрица
 Скачать 67.17 Kb. Скачать 67.17 Kb.
|
|
Линейная алгебра Лекция 4. Ранг матрицы Пусть имеется некоторая матрица 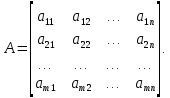 Если в матрице взять  строк и строк и  столбцов, то из элементов, стоящих на пересечении этих строк и столбцов, можно составить и вычислить определитель столбцов, то из элементов, стоящих на пересечении этих строк и столбцов, можно составить и вычислить определитель  того порядка. Будем называть такие определители минорами матрицы. того порядка. Будем называть такие определители минорами матрицы. Определение 1. Рангом матрицы 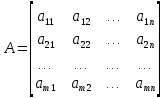 называется наивысший порядок минора матрицы, не равного нулю. Определение 1 требует, как правило, вычисления большого количества миноров матрицы. Следующая теорема позволяет несколько уменьшить это количество. Теорема 2. Пусть уже подсчитан минор  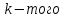 порядка, не равный нулю. Если все миноры порядка, не равный нулю. Если все миноры  порядка, окаймляющие минор порядка, окаймляющие минор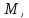 равны нулю, то ранг матрицы равен равны нулю, то ранг матрицы равен  (без доказательства). Из определения следует, что ранг ненулевой матрицы может изменяться от единицы до наименьшего из чисел 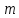 и и 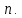 Надо сказать, что имеется и другое определение ранга матрицы, которое связано с понятием  мерных векторов и их линейной независимости. мерных векторов и их линейной независимости. Определение 2. Упорядоченное множество  чисел чисел  называется называется  мерным вектором. мерным вектором. Эти векторы можно: Умножать на число  Складывать  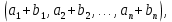 Вычитать 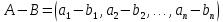 Скалярно умножать  Определение 3. Совокупность всех  мерных векторов с операциями 1) мерных векторов с операциями 1)  4) над ними называется 4) над ними называется мерным векторным пространством мерным векторным пространством 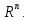 Определение 4. Система из нескольких  мерных векторов называется линейно зависимой, если один из этих векторов можно представить в виде линейной комбинации остальных векторов. В противном случае система векторов называется линейно независимой. мерных векторов называется линейно зависимой, если один из этих векторов можно представить в виде линейной комбинации остальных векторов. В противном случае система векторов называется линейно независимой.Пример 1. Система трех векторов  линейно зависима, так как 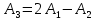 . .Для установления линейной зависимости и независимости более удобным является Определение 5. (эквивалентно определению 4) Система из нескольких  мерных векторов мерных векторов  называется линейно независимой, если равенство называется линейно независимой, если равенство  (1) (1)выполняется лишь в случае, когда 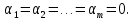 В противном случае, система называется линейно зависимой. Покажем, что система трех векторов  в примере 1 линейно зависима. Применим определение 5: 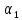 (3,2,1) (3,2,1)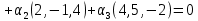 (2) (2) Расписав это равенство по компонентам (заметим, что в правой части стоит нулевой вектор!), получим систему линейных уравнений  Поменяв местами первое и третье уравнения, применим метод Гаусса:  Итак, последнее уравнение состоит из нулей, мы его отбрасываем. Из второго уравнения находим 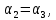 из первого уравнения находим из первого уравнения находим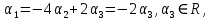 то есть имеем множество решений. Например, если взять значение 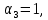 то соотношение (2) будет выглядеть следующим образом: то соотношение (2) будет выглядеть следующим образом: (3,2,1) (3,2,1) Отсюда видим, что вектор 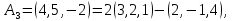 то есть, действительно является линейной комбинацией первых двух векторов. Пример 2. Покажем, что система трех векторов 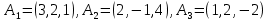 линейно независима. линейно независима.Применим определение 5: 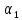 (3,2,1) (3,2,1)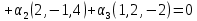 Расписав это равенство по компонентам (заметим, что в правой части стоит нулевой вектор!), получим систему линейных уравнений  Поменяв местами первое и третье уравнения, применим метод Гаусса: 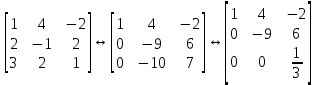 Последняя строка означает, что 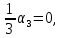 то есть имеем единственное решение то есть имеем единственное решение  Система векторов линейно независима. Определение 6. Рангом системы   мерных векторов называется максимальное число мерных векторов называется максимальное число 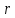 линейно независимых векторов. линейно независимых векторов. Определение 7. Подсистема 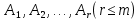 линейно независимых векторов системы  мерных векторов мерных векторов 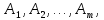 ранг которой равен ранг которой равен 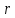 , называется базисом этой системы. , называется базисом этой системы.Теорема 3. Максимальное число линейно независимых  мерных векторов равно мерных векторов равно 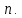 Для доказательства рассмотрим систему из  так называемых единичных векторов: так называемых единичных векторов: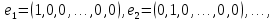 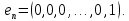 Нетрудно видеть, что любой  мерный вектор мерный вектор  есть линейная комбинация единичных векторов: есть линейная комбинация единичных векторов:  Следствие. Единичные векторы 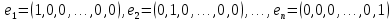 образуют базис линейного пространства 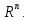 Определение 8. Рангом матрицы 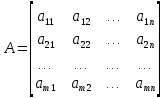 называется ранг системы  мерных векторов-строк этой матрицы. мерных векторов-строк этой матрицы.Для нахождения ранга матрицы применяется метод Гаусса, основанный на элементарных преобразованиях 1)  4) (см. лекцию 2) матрицы 4) (см. лекцию 2) матрицы  . . Теорема 4. Ранг матрицы не меняется при элементарных преобразованиях (без доказательства). Как мы уже знаем, метод Гаусса заключается в приведении матрицы  с помощью элементарных преобразований к матрице с помощью элементарных преобразований к матрице 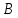 специального вида: специального вида: в которой все «диагональные» элементы 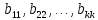 отличны от нуля, а элементы, расположенные ниже этих элементов, равны нулю. Нетрудно видеть, что ранг матрицы отличны от нуля, а элементы, расположенные ниже этих элементов, равны нулю. Нетрудно видеть, что ранг матрицы 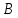 равен равен 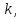 поскольку векторы-строки поскольку векторы-строки  этой матрицы линейно независимы. Действительно, из соотношения этой матрицы линейно независимы. Действительно, из соотношения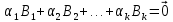 последовательно следует, что  Из теоремы 4 следует, что ранг исходной матрицы  также равен также равен  (если между какими – то строками исходной матрицы была линейная зависимость, то она исключалась путем вычеркивания нулевой строки). (если между какими – то строками исходной матрицы была линейная зависимость, то она исключалась путем вычеркивания нулевой строки). Пример 3. Найти ранг матрицы 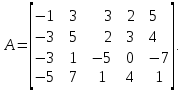 Решение. 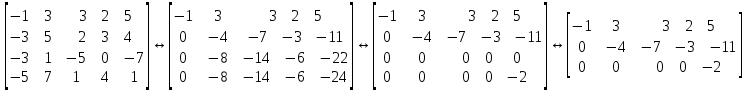 . .После перестановки местами третьего и пятого столбцов матрицы, мы получим структуру матрицы   . .Итак, ранг матрицы равен трем (третья строка  матрицы матрицы  оказалась линейной комбинацией первых двух строк: оказалась линейной комбинацией первых двух строк:  ). ).Вернемся к задаче решения линейной неоднородной системы уравнений 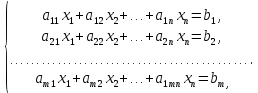 (3) (3) которой можно поставить в соответствие две матрицы 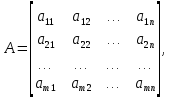  Первую матрицу, составленную из коэффициентов при неизвестных, будем называть основной матрицей, а вторую  расширенной матрицей. расширенной матрицей.Теорема Кронеккера  Капелли Капелли (о совместности линейной неоднородной системы). Система уравнений (3) совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы. Доказательство. Для простоты будем считать, что из системы уравнений (3) с помощью элементарных преобразований исключены все уравнения, являющиеся линейными комбинациями остальных уравнений, то есть приводящиеся к виду  (4) (4) Отметим, что в результате применения элементарных преобразований совместность (или несовместность) исходной системы не нарушена, поскольку получаются системы, ЭКВИВАЛЕНТНЫЕ исходной. Таким образом, без ограничения общности, можно считать, что система из расширенных векторов  (5) (5) линейно независима, то есть ранг этой системы равен  Это значит, по определению, что из равенства 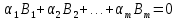 (6) (6)следует, что 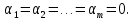 Предположим, что система (3) несовместна. Это, в соответствии с методом Гаусса, может быть только в том случае, когда некоторая линейная комбинация уравнений системы (3) имеет вид 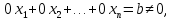 (7) (7) то есть, когда некоторая линейная комбинация строк матрицы  равна нулевому вектору, равна нулевому вектору, 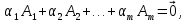 (8) (8) но эта же линейная комбинация из строк расширенной матрицы не равна нулевому вектору  (9) (9)Это значит, что из коэффициентов  хотя бы один не равен нулю, то есть система векторов хотя бы один не равен нулю, то есть система векторов  линейно зависима, а поэтому ранг основной матрицы меньше линейно зависима, а поэтому ранг основной матрицы меньше  Если система (3) совместна, то ранг системы строк матрицы  равен равен  то есть рангу системы строк расширенной матрицы то есть рангу системы строк расширенной матрицы  , так в этом случае из условия (8) обязательно следует условие , так в этом случае из условия (8) обязательно следует условие (10) (10) А это значит, что из линейной зависимости строк  (не все (не все  равны нулю) последует линейная зависимость строк равны нулю) последует линейная зависимость строк  что противоречит условиям (6). что противоречит условиям (6).Пример 4. Установить с помощью теоремы Кронеккера - Капелли, совместна ли система уравнений 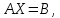 где где 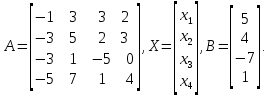 Как показано в примере 3, матрица  элементарными преобразованиями приводится к матрице элементарными преобразованиями приводится к матрице 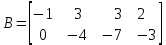 , ,То есть, ранг матрицы  равен двум. равен двум.Там же показано, что расширенная матрица  элементарными преобразованиями приводится к матрице  , ,То есть, ранг расширенной матрицы равен трем. Итак, система несовместна. Задания для самостоятельной работы. 1)Исследовать на линейную независимость систему векторов. 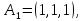 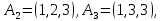 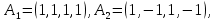 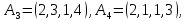 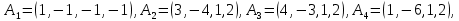 2)Найти ранг матрицы  3)Исследовать систему уравнений на совместность (два способа)  Исследовать на линейную независимость систему векторов. 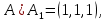 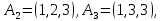 Применим определение 5: 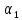 (1,1,1) (1,1,1) Расписав это равенство по компонентам (заметим, что в правой части стоит нулевой вектор!), получим систему линейных уравнений 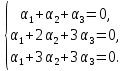 Применим метод Гаусса: 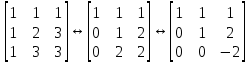 Последнее уравнение имеет вид:  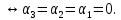 Система векторов линейно независима.  Применим определение 5: 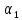 (1,1,1,1) (1,1,1,1)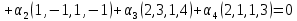 Расписав это равенство по компонентам, получим систему линейных уравнений  Применим метод Гаусса: 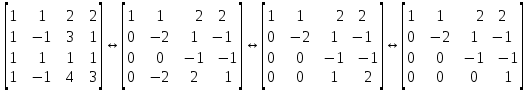 Последнее уравнение имеет вид: 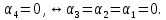 Система векторов линейно независима. C) 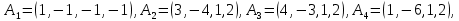 Применим определение 5: 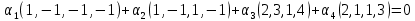 Расписав это равенство по компонентам, получим систему линейных уравнений  Применим метод Гаусса: 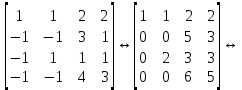 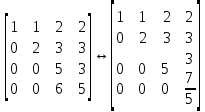 Последнее уравнение имеет вид: 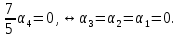 Система векторов линейно независима. Найти ранг матрицы  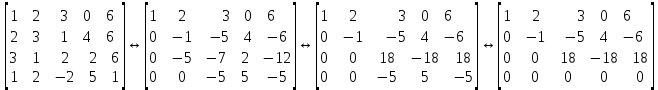 Ранг матрицы равен трем. Исследовать систему уравнений на совместность (два способа)  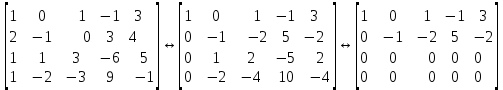 Последнее уравнение имеет вид: 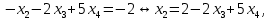 Система совместна, имеет множество решений. Способ 2.  Ранг матрицы Ранг матрицы  равен двум. равен двум.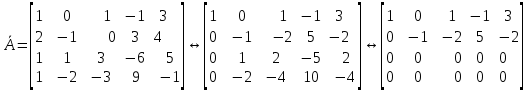 Ранг расширенной матрицы  равен тоже двум. Система совместна. равен тоже двум. Система совместна.Лекция 5. 1.Однородные системы, фундаментальная система решений. Рассмотрим вопрос о множестве решений однородной системы линейных уравнений 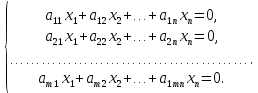 (1) (1)Как мы знаем, если ранг матрицы равен  то эту систему с помощью элементарных преобразований можно привести к эквивалентной системе вида то эту систему с помощью элементарных преобразований можно привести к эквивалентной системе вида (2) (2)в котором последнее уравнение может иметь лишь один из следующих двух вариантов: 1)Оно имеет вид 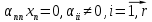 то есть является уравнением с одним неизвестным то есть является уравнением с одним неизвестным 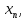 которое однозначно находится: которое однозначно находится: 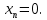 В этом случае исходная система имеет ЕДИНСТВЕННОЕ решение В этом случае исходная система имеет ЕДИНСТВЕННОЕ решение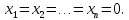 2)Оно содержит несколько переменных, то есть имеет вид 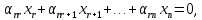 в этом случае исходная система имеет бесчисленное множество решений. Для того, чтобы описать это множество решений, полезно ввести понятие фундаментальной системы решений. Будем называть переменные  базовыми переменными, а переменные базовыми переменными, а переменные  свободными переменными. Каждому набору свободных переменных свободными переменными. Каждому набору свободных переменных  соответствует единственное решение системы (1): соответствует единственное решение системы (1): - набору 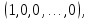 образующему единичный образующему единичный 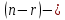 мерный вектор мерный вектор  соответствует решение соответствует решение 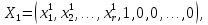 - набору 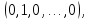 образующему единичный образующему единичный 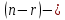 мерный вектор мерный вектор 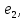 соответствует решение соответствует решение 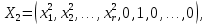 и так далее…. наконец, и так далее…. наконец, - набору 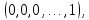 образующему единичный образующему единичный 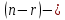 мерный вектор мерный вектор  соответствует решение соответствует решение 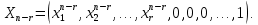 Определение 1. Набор указанных выше решений 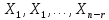 называется фундаментальной системой решений однородной системы уравнений (1). называется фундаментальной системой решений однородной системы уравнений (1).Теорема 1. Любое решение однородной системы алгебраических уравнений (1) является линейной комбинацией решений, входящих в фундаментальную систему решений. Доказательство. Пусть  некоторое решение системы (1). Покажем, что при определенном выборе произвольных констант некоторое решение системы (1). Покажем, что при определенном выборе произвольных констант  имеет место равенство: имеет место равенство: 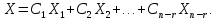 (3) (3)Во-первых, заметим, что в силу однородности и линейности системы (1) любая линейная комбинация решений также является решением, то есть в правой части соотношения (3) стоит решение системы (1). Далее, если в качестве произвольных констант выбрать значения  то то  мерный вектор мерный вектор 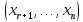 будет линейной комбинацией единичных векторов будет линейной комбинацией единичных векторов 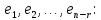  Так как решение системы (1) однозначно определяется выбором свободных переменных 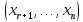 , то решение , то решение  совпадает с решением совпадает с решением  что и требовалось доказать. что и требовалось доказать. Следствие. Общее решение неоднородной системы линейных алгебраических уравнений является суммой общего решения соответствующей однородной системы и любого частного решения неоднородной системы. Пример 1. Найти общее решение однородной системы  (4) (4)Применяем метод Гаусса: 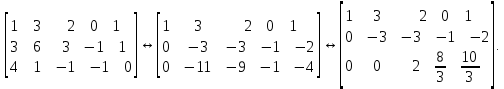 Итак, последнее уравнение имеет вид: 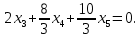 Положив 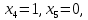 получим решение получим решение 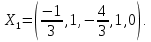 Положив 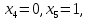 получим решение получим решение  Таким образом, общее решение системы (4) имеет вид: 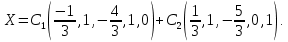 Пример 2. Найти общее решение неоднородной системы 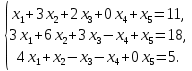 (5) (5)Применяем метод Гаусса:  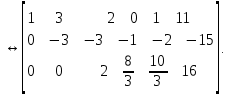 Итак, последнее уравнение имеет вид: 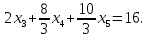 Положив 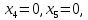 получим частное решение неоднородной системы (5): получим частное решение неоднородной системы (5): Соответственно, с учетом примера (1) общее решение системы (5) имеет вид:  Пример 3. Найти общее решение неоднородной системы  Сначала находим общее решение соответствующей однородной системы  Применяем метод Гаусса:  Итак, последнее уравнение имеет вид:  (свободная переменная). (свободная переменная).Находим базисный вектор, задав  Итак, общее решение однородной системы имеет вид:  Находим решение неоднородной системы: 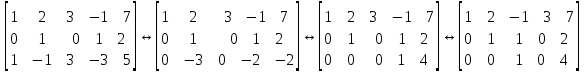 Итак, последнее уравнение имеет вид: 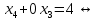 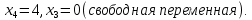 Находим частное решение неоднородной системы: 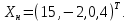 В результате получаем общее решение неоднородной системы: 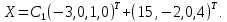 Например, при  имеем решение имеем решение  2.Собственные значения и векторы матрицы. Определение 2. Число  называется собственным значением квадратной матрицы называется собственным значением квадратной матрицы  размерами размерами  если существует такой ненулевой вектор если существует такой ненулевой вектор 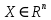 , что имеет место равенство , что имеет место равенство (6) (6)Вектор  при этом называется собственным вектором матрицы при этом называется собственным вектором матрицы  Отметим, что собственный вектор определяется с точностью до постоянного множителя: если вектор  удовлетворяет соотношению (6), то и любой вектор удовлетворяет соотношению (6), то и любой вектор 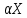 тоже удовлетворяет соотношению (6). тоже удовлетворяет соотношению (6). Для нахождения собственных значений и собственных векторов матрицы  удобнее использовать соотношение удобнее использовать соотношение 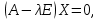 (7) (7)которое равносильно равенству (6). Пример 3. Найти собственные числа и собственные векторы матрицы 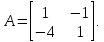 Составим матрицу  и ибудем искать ненулевое решение однородной системы уравнений: 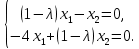 (8) (8)Как мы знаем, если основной определитель системы не равен нулю, то система имеет единственное решение (в данном случае нулевое). Поэтому ненулевое решение может существовать лишь при условии, что основной определитель системы равен нулю: 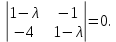 Раскрывая определитель, получим уравнение для собственных значений матрицы: 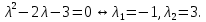 Подставляя в систему (8) значение 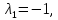 получим уравнение для нахождения собственного вектора получим уравнение для нахождения собственного вектора  : :  Как уже было сказано, собственный вектор определяется с точностью до константы, например  Подставляя в систему (8) значение  получим уравнение для нахождения собственного вектора получим уравнение для нахождения собственного вектора 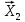 : :  Как уже было сказано, собственный вектор определяется с точностью до константы, например 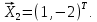 Задания для самостоятельной работы. Найти собственные числа и собственные векторы матрицы 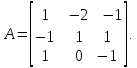 |
