Математическая Модель - графический метод. мат.модель. Построение мат модели и решение задач тпр

• Название: Построение мат модели и решение задач тпр
• Анкор: Математическая Модель - графический метод
• Дата: 23.09.2020
• Размер: 433.86 Kb.
• Имя файла: мат.модель.docx
• Тип: Решение; #139200

Коцур Диана АСОиУ(б)-18-1

Контрольная работа №1

Тема: Построение мат. модели и решение задач ТПР

Вариант:

1. 
   Управляемые переменные
   

В задаче необходимо определить кол-во краски каждого вида для производства.

• 
  X(E) - суточный объем производства краски Е (т)
  
• 
  X(I)- суточный объем производства краски I (т).
  

2. 
   Целевая функция
   

Так как стоимость 1 т краски Е равна 3 тыс. долл., суточный доход от ее продажи составит 3 x(E) тыс. долл. Аналогично доход от реализации x(I) тонн краски I составит 2 x(I) тыс. долл. в сутки. ->

Определить допустимые значения УП x(Е) и x(I), максимизирующие величину общего дохода.

3. 
   Ограничения
   

А) Ограничение на расход исходных продуктов для 2 видов краски ≤ максимально возможного запаса данного исходного продукта:
- А
- В
Б) Ограничения на величину спроса красок:

Превышение спроса на краску I относительно краски E ≤ 1 тонне 1 сутки

Спрос на краску I ≤ 2 тонны 1 сутки:
- соотношение I и Е
- максимальная величина спроса I
Переменные xI и xE не могут принимать отрицательных значений:
- объем производства краски I,
- объем производства краски Е.
4) Математическая модель
Определить суточные объемы производства (xI и xE ) краски I и краски Е, при которых достигается максимум (по целевой функции).
при ограничениях: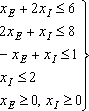




5) Решение графически

1. 
   построение области допустимых решений.
   
2. 
   уравнение линий уровня 3 x(Е) +2 x(I)=a (a – любое вещественное число)
   
3. 
   построим линию уровня
   
4. 
   найдем f ‘(0) = (3,2)
   
5. 
   переместим линию уравнения в направлении вектора до получения первой точки пересечения линии уравнения с ОДР.
   

1

с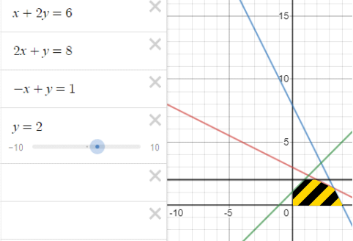


Рисунок 1 - ОДР

Полученные уравнения из неравенств задают на плоскости прямые.

Чтобы изобразить прямую 1го неравенства, найду две точки, лежащие на этой прямой - 6,0, 0,3, и проведу через них прямую. Аналогично, прямая 2го неравенства проходит через точки 4,0 и 0,8, 3го 1,0 и 0,1, 4го  2 параллельна оси Ox(E) и проходит через точку 0,2.

Определяем, с какой стороны от прямой находится область, удовлетворяющая каждому неравенству. Точки, удовлетворяющие всем ограничениям и ограничениям на знак переменных x(E)  0 , x(I)  0 образуют множество допустимых решений задачи ЛП (закрашенный многоугольник на рисунке 1)

6. 
   Исходя из ОДР найдем максимал. доход.
   

Оптимальному решению соответствует точка O. Так как точка O является точкой пересечения прямых, то значения хЕ и xI в этой точке определяются решением системы уравнений первых 2х неравенств.
Можно показать, что   Полученное решение означает, что суточный объем производства краски Е должен быть равен 3.1/3 т, а краски I - 3.1/3 т.
Доход составит  (тыс. дол.)

Ответ: тыс. дол.