теория цифровой обработки сигналов. РЕФЕРАТ. Построение спектра сигнала
 Скачать 219.5 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет» Аэрокосмический факультет Кафедра «Ракетно-космическая техника и энергетические системы» направление 13.03.03– Энергетическое машиностроение Дисциплина «Теория цифровой обработки сигналов» Реферат «Построение спектра сигнала» Выполнил: ст. гр. ГПУД 17-1б/з Мартюченко В.О. Проверил: ст. преподаватель, Матюнин О. О. Пермь 2022 Содержание Введение…………………………………………………………………………..3 Спектральное представление сигналов……………………………..………..4 Спектральное представление периодических, гармонических сигналов………………………………………………………………………….5 Спектральное представление периодических, негармонических сигналов………………………………………………………………………………………..7 Спектральное представление непериодических сигналов………..………11 Список литературы……………………………………………………….……14 Введение. Чтобы подобраться к понятию спектра сигнала поясним, что такое сигнал. Сигнал – материальный носитель информации. Для сигнала характерно изменение физической величины со временем. Математическая модель сигнала это функция от времени S(t). Что такое спектр сигнала? Для нас привычно наблюдать какие либо изменения с течением времени. Представим сигнал не во временной области, а в частотной. Математическая модель спектра это функция от частоты F(f). Спектр сигнала — это совокупность простых составляющих сигнала с определенными амплитудами, частотами и начальными фазами. Существует два вида спектральных диаграмм: - спектральная диаграмма амплитуд - спектральная диаграмма фаз. В спектральной диаграмме амплитуд - отображаются все составляющие со своими амплитудами и частотами. В спектральной диаграмме фаз - отображаются все составляющие со своими начальными фазами и частотами. Представим простейший синусоидальный сигнал и его графики амплитудно и фазо-частоной характеристик: 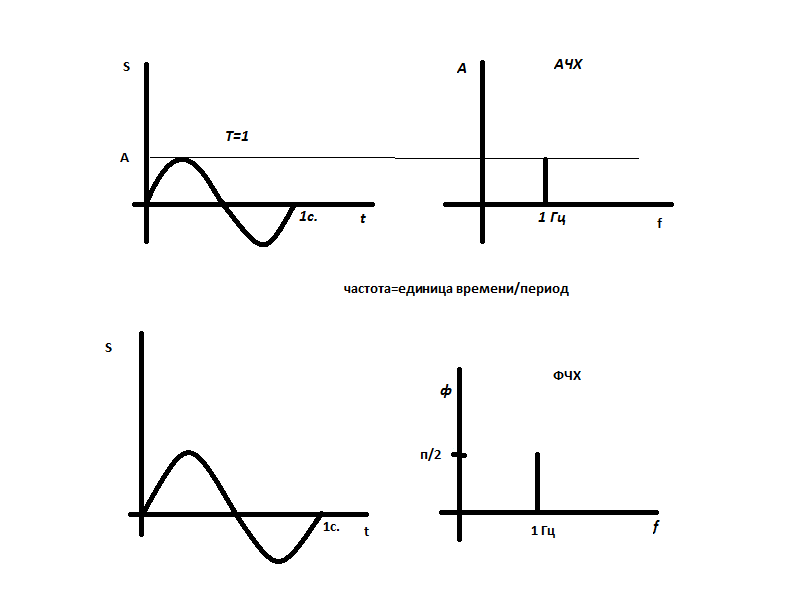 совокупность ФЧХ и АЧХ это и есть спектр сигнала. Спектральное представление сигналов. Любой сигнал можно разложить на составляющие. Такое разложение сигнала называется спектральным. При этом сигнал можно представить в виде графика зависимости параметров сигнала от частоты, такая диаграмма называется спектральной или спектром сигнала. Спектр сигнала - это совокупность простых составляющих сигнала с определенными амплитудами, частотами и начальными фазами. Между спектром сигнала и его формой существует жесткая взаимосвязь: изменение формы сигнала приводит к изменению его спектра и наоборот, любое изменение спектра сигнала приводит к изменению его формы. Это важно запомнить, поскольку при передаче сигналов в системе передачи, они подвергаются преобразованиям, а значит, происходит преобразование их спектров. Различают два вида спектральных диаграмм: - спектральная диаграмма амплитуд; - спектральная диаграмма фаз. В спектральной диаграмме амплитуд - отображаются все составляющие со своими амплитудами и частотами. В спектральной диаграмме фаз - отображаются все составляющие со своими начальными фазами и частотами. Любой сигнал имеет одну спектральную диаграмму амплитуд и одну спектральную диаграмму фаз, в составе которых может содержаться множество составляющих. Не зависимо от того, какой спектр (амплитуд или фаз), он изображается в виде множества линий - составляющих. В спектре амплитуд высота спектральной линии равна амплитуде составляющей сигнала, а в спектре фаз - начальной фазе составляющей. Причем: в спектре амплитуд все составляющие имеют положительные значения, а в спектре фаз как положительные, так и отрицательные. Если амплитуда спектральной составляющей имеет отрицательный знак, то в спектре амплитуд она берется по модулю, а в спектре фаз знак составляющей изменяется на противоположный. По виду спектры бывают дискретными (линейчатыми) или сплошными. Дискретным является спектр, у которого можно выделить отдельные составляющие. Сплошным является спектр, у которого нельзя выделить отдельные составляющие, так как они расположены настолько близко, что сливаются друг с другом. Спектральное представление периодических, гармонических сигналов Математическая модель гармонического колебания имеет вид: x(t)=5*sin(wt+1) Как видно из математической модели, в спектре данного колебания присутствует одна гармоническая составляющая, которая находится на частоте  . Высота составляющей в спектре амплитуд равна амплитуде колебания 5, а в спектре фаз - начальной фазе колебания 1. Причем при построении спектра необходимо учитывать связь между временной диаграммой сигнала и спектром амплитуд. Амплитуда составляющей спектра должна по высоте соответствовать амплитуде колебания на временной диаграмме. график сигнала  диаграмма АЧХ  диаграмма ФЧХ Спектральное представление периодических, негармонических сигналов. Математическая модель негармонического колебания имеет вид:  Основной особенностью спектрального представления таких сигналов является наличие в их спектре множества спектральных составляющих. Такие сигналы могут быть описаны рядом Фурье. Представим периодический сигнал наиболее распространенной в теории сигналов тригонометрической (синусно-косинусной) формой ряда Фурье:  (1)компоненты анализируемого сигнала: - постоянная составляющая (2) - амплитуды косинусоидальных составляющих: (3) - амплитуды синусоидальных составляющих: (4) 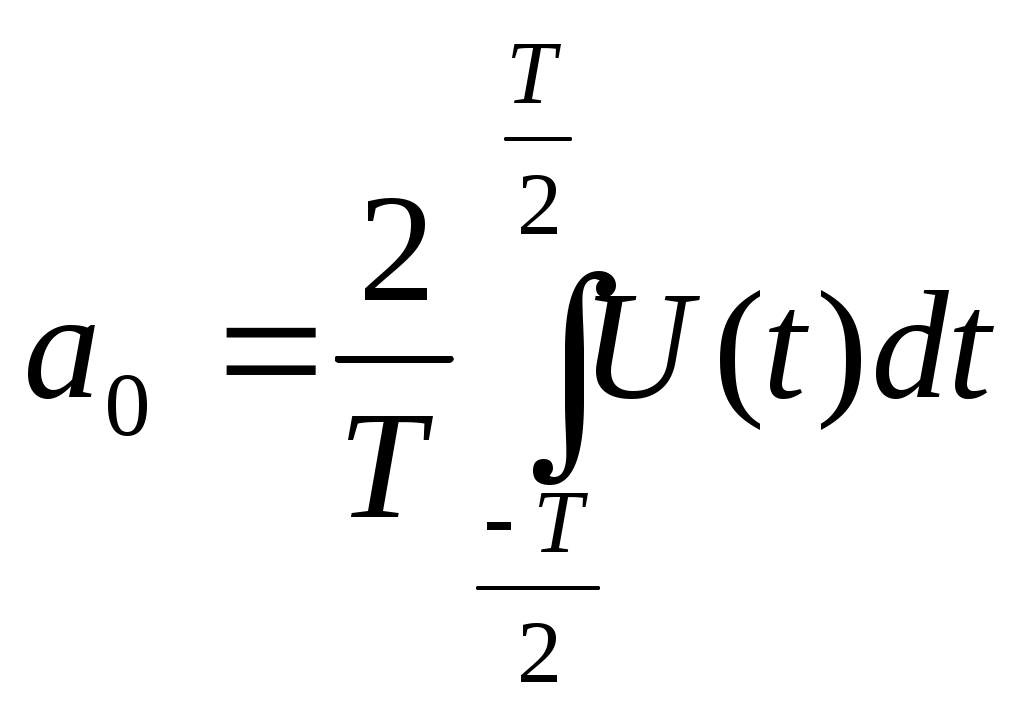 (2) (3) (4)Спектральную составляющую с частотой ω1 в радиотехнике называют первой (основной) гармоникой, а составляющие с частотами k  1 (k> 1) - высшими гармониками периодического сигнала.Если сигнал представляет собой четную функцию времени U(t) = U(-t), то в тригонометрической записи ряда Фурье (1) отсутствуют синусоидальные коэффициенты bk так как в соответствии с формулой (4) они обращаются в нуль. Для сигнала U(t), описываемого нечетной функцией времени, наоборот, согласно формуле (3), нулю равны косинусоидальные коэффициенты аk и ряд содержит составляющие bn (кстати, постоянная составляющая а0 также отсутствует). Заметим, что пределы интегрирования (от -T/2 до T/2) не обязательно должны быть такими, как в приведенных формулах (2 - 4). Интегрирование может производиться по любому интервалу времени шириной T- результат от этого не изменится. Часто применение синусно-косинусной формы ряда Фурье не совсем удобно, поскольку для каждого значения индекса суммирования (т. е. для каждой гармоники с частотой k 1) в формуле (1) фигурируют два слагаемых: косинус и синус. С математической точки зрения удобнее эту формулу представить эквивалентным рядом Фурье в вещественной форме:  (5)   где : Аk - амплитуда;  k- начальная фаза k-й гармоники сигнала.Также широко используют комплексную форму ряда Фурье. Она получается из вещественной формы ряда представлением косинуса в виде полусуммы комплексных экспонент. Представление вытекает из формулы Эйлера: еjх = cosx +jsinx:  Применив данное преобразование к вещественной форме ряда Фурье (5), получим суммы комплексных экспонент с положительными и отрицательными показателями:  (6)А теперь будем трактовать в (6) экспоненты при частоте ω1 со знаком минус в показателе как члены ряда с отрицательными номерами. В рамках этого же подхода коэффициент А0 станет членом ряда с нулевым номером. После преобразований приходим к комплексной форме ряда Фурье:  (7)где  (8)- комплексная амплитуда k-й гармоники. Cвязь между коэффициентами тригонометрической и комплексной форм ряда Фурье.   (9)Можно также показать, что коэффициенты:   (10)Если U(t) является четной функцией, коэффициенты ряда Сk будут вещественными, а если U(t) - функция нечетная, коэффициенты ряда станут мнимыми. Из формулы (7) нетрудно выяснить, что спектральное представление периодического сигнала комплексной формой ряда Фурье содержит как положительные, так и отрицательные частоты. Однако отрицательные частоты в природе не существуют, и это не физическое понятие, а математическая абстракция (физический смысл отрицательной частоты - вращение в направлении, противоположном тому, которое принято за положительное). Они появляются как следствие формального представления гармонических колебаний комплексной формой.  график сигнала  диаграмма АЧХ  амплитудный спектр комплексного ряда Фурье Спектральное представление непериодических сигналов. Математическая модель непериодического колебания имеет вид:  Для радиотехники интерес представляют импульсные (одиночные) сигналы. Преобразование Фурье является инструментом спектрального анализа непериодических (импульсных) сигналов (их еще называют сигналами конечной длительности, или финитными, т. е. пространственно ограниченными). Положим, что некоторая функция U(t) аналитически описывает одиночный импульсный сигнал конечной длительности. Мысленно дополнив его такими же импульсными сигналами. Для того чтобы вне искусственно введенного интервала времени 0 ... Т исходный сигнал был равен нулю, необходимо увеличить период повторения этих импульсов. В пределе, при увеличении длительности периода и Т  , все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность импульсов Uk(t) вновь станет одиночным импульсом U(t). В этом случае выражения (7) и (8) сохраняют смысл. Подставив соотношение (8) в формулу (7), запишем периодическую функцию: (11)Так как период следования импульсов Т= 2π/ 1 то: (12)В предельном случае, когда Т , равные расстояния между спектральными линиями уменьшатся настолько, что спектр станет сплошным, а амплитуды отдельных спектральных составляющих окажутся бесконечно малыми. При этом частота следования импульсов 1 = 2 /Т  0 и превращается в d , дискретная переменная k 1 - в мгновенную (текущую) частоту , а сумма трансформируется в интеграл. Периодическая последовательность импульсов Uk(t) станет одиночным импульсом U(t), и выражение (12) запишется в виде: Интеграл в скобках есть комплексная функция частоты. Обозначив его:  (13)Получим:  (14)Соотношения (13) и (14) носят фундаментальный характер в теории сигналов и определяют соответственно прямое и обратное преобразования Фурье. Они связывают между собой вещественную функцию времени U(t) и комплексную функцию частоты S( ). Если использовать не угловую частоту со, а циклическу f = /(2π), то формулы прямого (13) и обратного (14) преобразования Фурье становятся еще более симметричными, отличаясь лишь знаком в показателе: (15) (16) прямоугольный импульс временная диграмма  модуль спектральной плотности Список литературы: Сергиенко А. Б. Цифровая обработка сигналов: учебное пособие.- 3-изд. – СПб.: БХВ - Петербург, 2011. – 768 с. Якимов Е. В. Цифровая обработка сигналов: учебное пособие/ Е. В. Якимов, Г. В. Вавилова, И. А. Клубович. – Томск: изд-во Томского политехнического университета, 2008. – 307 с. |