лабораторная матлаб. Отчет. Построение управления с интерактивным обучением
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского» Институт информационных технологий, математики и механики Направление подготовки: «Прикладная математика и информатика» Профиль подготовки: «Математическое моделирование динамики систем и процессов управления» Практическое задание №1 по дисциплине «Робастное управление» «Построение управления с интерактивным обучением» Выполнили: Балашов А.А. Куликов Д.А. Зеленцов Н.Г. Проверил: преподаватель Пакшин П.В. Нижний Новгород 2022 г. Содержание Теоретические сведения 2 Порядок выполнения работы 3 Заключение 9 Список использованных источников 10 Построить модель системы интерактивного управления с обучением для портального робота из [1, стр. 193]. Теоретические сведенияВ рассматриваемой задаче рассматривается пример эксперимента с автоматизацией портального робота из лаборатории Саутгемптонского университета. Задачей робота является установка предметов из условного «ящика» на конвейерную ленту с заданной точностью. Управление роботом осуществляется по сигналам обратной связи в ортогональной системе координат x-y-z. Рассмотрим интерактивное управление по оси y – горизонтальной оси трехмерной системы. На рисунке 1 показана траектория желаемого перемещения – участок синусоиды. 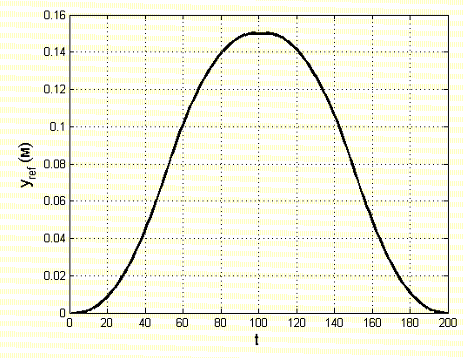 Рисунок 1 – Проекция траектории по оси y Передаточная функция электропривода горизонтальной степени свободы робота:
Для реализации управления будем рассматривать дискретизированную систему с шагом дискретизации 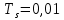 с. с.Дискретную модель получим, введя передаточную функцию в MatLab в виде объекта tf. Затем преобразуем объект в пространство состояний State Space (ss), а затем, дискретизуем модель функцией c2d. Мерой точности является ошибка обучения.
где ek – значение ошибки в момент времени t. N – количество отсчетов. Порядок выполнения работыУравнение объекта в непрерывном пространстве состояний для решения задачи воспользуемся следующими зависимостями:
Дискретизация приводит к замене в (2) непрерывного времени дискретным nΔTс Приращение дискретного управления определяется из закона:
Ошибка интерактивного обучения определяется, как разность выходного управления на текущем и предыдущем шагах:
При интерактивном управлении закон управления определяется выражением:
Где Ki – вычисляемые в процессе интерактивного обучения коэффициенты управления. Как видим, управление линейное. 2. Численный эксперимент проводился при следующих условиях. Матрицы Qи R имеют следующий вид: 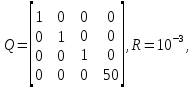 Число шагов интегрирования изменяется от 1 до 100, время интегрирования – от 0 до 200 с. В итоге было получено управление 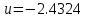 , при этом , при этом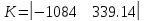 Как видно из рис. 3, среднеквадратическая ошибка уменьшается в 10 раз менее чем за 15 повторений. Для получения коэффициентов численного эксперимента, напишем функцию Calculate_K.m, текст которой приведен ниже function out = calculateK(A,B,C,Q,R) %Задаем начальное приближение коэффициентов A_ = [[A;-C*A] [zeros(3,1);eye(1)]]; B_ = [B;-C*B]; C_ = [[C;zeros(1,3)] [zeros(1);eye(1)]]; % Вычисляем матрицы для работы пакета yalmip - матрицы цели и начальных % условий X = sdpvar(4, 4); Y = sdpvar(1, 2); Z = sdpvar(2, 2); %Рассчитываем матрицы коэффициентов метода наименьших квадратов n11 = X; n12 = (A_*X+B_*Y*C_)'; n13 = X; n14 = (Y*C_)'; part1 = [[n11 n12] [n13 n14]]; %Находим целевые матрицы n21 = A_*X+B_*Y*C_; n22 = X; n23 = zeros(4,4); n24 = zeros(4,1); %Матрицы начальных приближений n31 = X; %Вектор начальных условий n32 = zeros(4,4); %Нулевая матрица для записи коэффициентов n33 = inv(Q); n34 = zeros(4,1); % part2 = [[n21;n31] [n22;n32] [n23;n33] [n24;n34]]; n41 = Y*C_; n42 = zeros(1,4); n43 = zeros(1,4); n44 = inv(R); part3 = [[n41 n42] [n43 n44]]; LMN = [part1;part2;part3]; %Настраиваем параметры модуля решения Constraints = [LMN >= 0, C_*X == Z*C_, X >= 0]; %Блок получения решения %Запуск процедуры оптимизации optimize(Constraints, [], sdpsettings('verbose',0)); %Сохранение коэффициентов робастного управления K = value(Y) * inv(value(Z)); out = K; end Результат тестирования функции показан на рис. 2 и рис. 3. 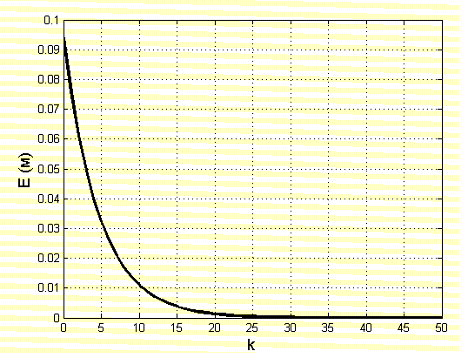 Рисунок 2 - Изменение среднеквадратической ошибки обучения в зависимости от числа повторений Ниже приведен текст основной программы, и результаты ее работы %Задаем коэффициенты исходной системы управления% a1 = 426.7; a2 = 1.744 * 10^5; a3 = 0; c1 = 0; c2 = 23.7356; c3 = 661.2*23.7356; % Расчетные значения матриц системы A = [ 0, 1, 0; 0, 0, 1; -a3, -a2, -a1; ]; B = [0; 0; 1]; C = [c3, c2, c1]; %Рассчитываем дискретную систему D=[0]; %Задаем систему в пространстве состояний SYSC=ss(A,B,C,D); TS=0.01; %Шаг дискретизации SYSD = c2d(SYSC,TS,'zoh'); %Выполняем дискретизацию системы %Извлекаем из объекта значения дискретных матриц A=SYSD.a; B=SYSD.b; C=SYSD.c; D=SYSD.d; Q = diag([1 1 1 50]); R = 10^(-3); %Рассчитываем коэффициенты робастного управления K = calculateK(A,B,C,Q,R); x_k = zeros(3,1); k_max = 100; %Число шагов алгоритма t_max = 200; %Время моделирования k_range = 0:k_max; t_range = 0:t_max; y_ref = sin(t_range / (t_max / pi)) * 1.0/7.0; %Входное гармоническое воздействие f1 = figure; %Строим график гармонического воздействия figure(f1); plot(t_range, y_ref) xlabel('t') ylabel('Yref (Рј)') E = []; Y = zeros(length(k_range), length(t_range)); U = zeros(length(k_range), length(t_range)); E_K_ = zeros(length(k_range), length(t_range)); %Готовим массивы для 3D-графика for k = 2:length(k_range) E_k = []; for t = 1:length(t_range)-1 Y(k,t) = C*x_k; U(k,t) = U(k-1,t)+K(1)*(Y(k,t)-Y(k-1,t))+K(2)*(y_ref(t+1)-Y(k-1, t+1)); x_k_next = A*x_k + B*U(k,t); x_k = x_k_next; e_k = y_ref(t) - Y(k,t); E_K_(k,t) = e_k; E_k = [E_k, e_k]; end E_k = E_k.^2; E_k = (sum(E_k)/length(E_k))^0.5; E = [E, E_k]; end %Строим графики f2 = figure; figure(f2); plot(0:length(E)-1, E); ylim([0 0.1]); xlim([0 100]); xlabel('k') ylabel('E (Рј)') grid on [T_,K_] = meshgrid(t_range, k_range); f3 = figure; figure(f3); surf(T_, K_, U) xlabel('t') ylabel('k') zlabel('u') shading interp f4 = figure; figure(f4); surf(T_, K_, Y) xlabel('t') ylabel('k') zlabel('y') shading interp f5 = figure; figure(f5); s = surf(T_, K_, E_K_); xlabel('t') ylabel('k') zlabel('e (Рј)') shading interp 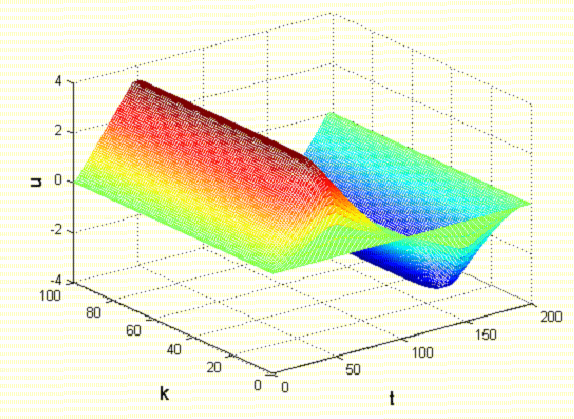 Рисунок 1 - Изменение управляющего воздействия в зависимости от числа повторений 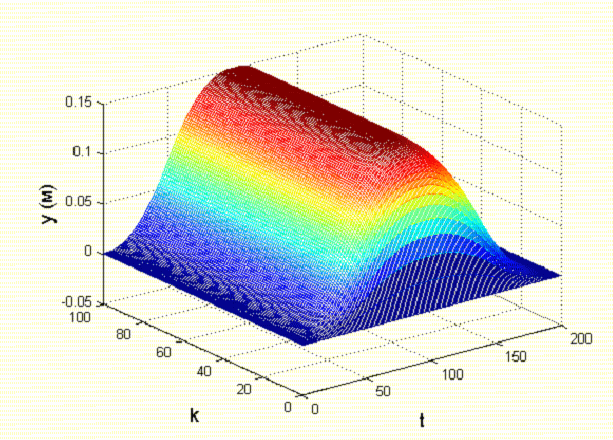 Рисунок 5 - Изменение выходной переменной в зависимости от числа повторений 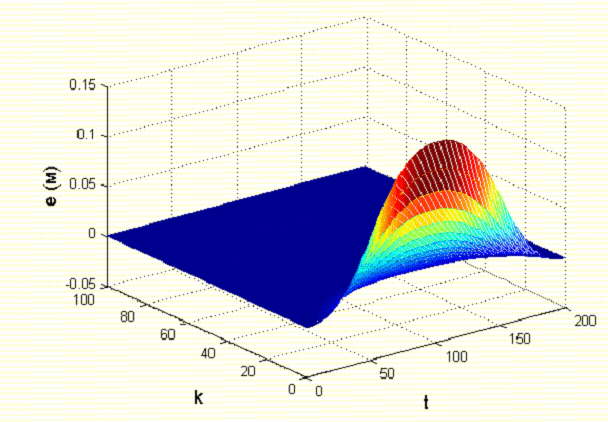 Рисунок 6 - Изменение ошибки обучения в зависимости от числа повторений ЗаключениеВ ходе лабораторной работы было построено оптимальное интерактивное управление с обучением для управления одной из координат электропривода робота. Достигнут минимум среднеквадратической ошибки. Метод интерактивного обучения показал достаточно высокие результаты по скорости сходимости и достижения необходимого функционала качества. Список использованных источниковЕмельянова Ю.П., Пакшин П.В. УПРАВЛЕНИЕ С ИТЕРАТИВНЫМ ОБУЧЕНИЕМ https://yalmip.github.io/ |

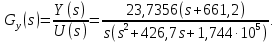
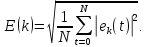
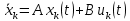
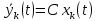
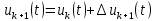
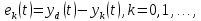
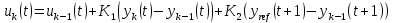 .
.