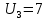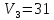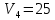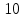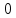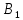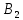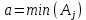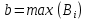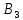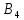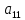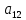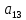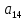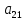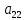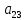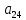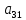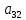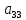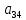Вар9. Построим графики линейных функций
 Скачать 120.77 Kb. Скачать 120.77 Kb.
|
|
План не оптимальный, так как 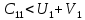 . .
План не оптимальный, так как 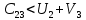 . .
План оптимальный, так как 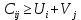 . .План заполнен методом наименьшего элемента. 4.9. Найти наибольшее и наименьшее значения функции 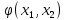 в заданной области графическим методом. Применить метод множителей Лагранжа для поиска наименьшего значения этой функции. в заданной области графическим методом. Применить метод множителей Лагранжа для поиска наименьшего значения этой функции.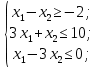 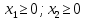 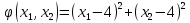 Построим графики линейных функций. 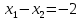
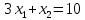
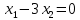
Решением функции 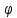 будет являться окружность с центром (4;4). Наибольшее значение функции достигается в точке А. Найдем координаты этой точки. будет являться окружность с центром (4;4). Наибольшее значение функции достигается в точке А. Найдем координаты этой точки.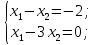 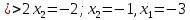 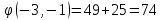 Наименьшим значением будет пересечение с окружности с центром (4;4) с прямой 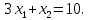 Поскольку прямая OB перпендикулярна прямой 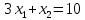 , то ее уравнение имеет вид , то ее уравнение имеет вид 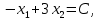 так как OB проходит через точку (4;4), то так как OB проходит через точку (4;4), то 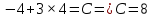 . .Тогда OB имеет вид: 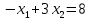 . .Составим систему уравнений. 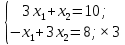  Метод множителей Лагранжа. 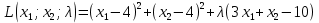 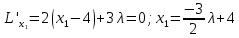 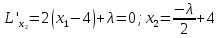 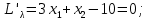 Подставим значения 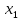 и и 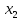 : :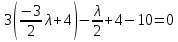 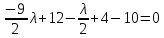 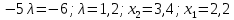 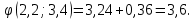 Ответ: 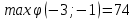 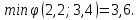 5.9. Определить нижнюю и верхнюю цену игры, найти оптимальное решение и цену игры, заданной матрицей. 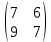
Найдем нижнюю цену игры, 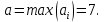 Верхняя цена игры - 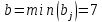 , , 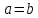 , значит седловая точка (2;2) указывает решение. Цена игры равна 7. , значит седловая точка (2;2) указывает решение. Цена игры равна 7.6.9. Предприятие может оказывать транспортные услуги трех видов 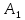 , , 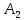 , , 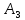 , получая при этом прибыль, зависящую от спроса, который может находиться в одном из четырех состояний , получая при этом прибыль, зависящую от спроса, который может находиться в одном из четырех состояний 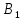 , , 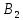 , , 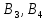 . .
Элементы матрицы характеризуют величину прибыли 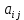 , которую получит предприятие, если будет оказывать i-й вид транспортных услуг при j-м состоянии спроса на эти услуги. , которую получит предприятие, если будет оказывать i-й вид транспортных услуг при j-м состоянии спроса на эти услуги.Необходимо определить оптимальные пропорции оказываемых предприятием видов услуг, реализация которых обеспечила бы ему максимально возможную выручку независимо от состояния спроса. 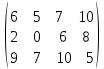  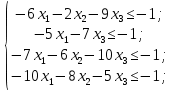  Составим систему неравенств.  Приведем систему неравенств к виду « | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

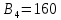
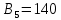
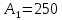
 36
36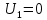
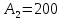
 26
26 35
35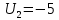
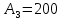
 35
35 42
42 39
39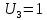
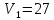
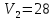
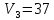
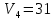
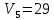
 42
42