КТ 2 Построение циклических кодов. Построить порождающую и проверочную матрицы этого кода в систематическом виде

• Название: Построить порождающую и проверочную матрицы этого кода в систематическом виде
• Дата: 26.05.2022
• Размер: 1.25 Mb.
• Имя файла: КТ 2 Построение циклических кодов.docx
• Тип: Документы; #550662

Задание 1. Построить код Хемминга с заданным числом k информационных разрядов, гарантированно исправляющий все одиночные ошибки и обнаруживающий q независимых ошибок. Следует выбирать код, обеспечивающий при данных условиях максимальную скорость передачи.

Построить порождающую и проверочную матрицы этого кода в систематическом виде.

Оценить основные информационные характеристики этого кода.

Привести пример кодирования и декодирования (в матричном виде) в случае отсутствия ошибки и в случае исправления ошибки.

Параметры кода выбираются из таблицы 1 в соответствии с вариантом выполнения задания. Вариант определяется порядковым номером студента в официальном списке группы.

Таблица 1 – Варианты выполнения задания 1

вариант	k	q	примитивный полином №	вариант	k	q	примитивный полином №
1	7	1	2	14	7	1	1
2	9	2	2	15	10	1	2
3	4	1	2	16	8	2	2
4	8	1	2	17	3	2	2
5	10	2	1	18	9	1	2
6	11	1	2	19	11	2	1
7	3	1	2	20	7	2	1
8	8	2	1	21	6	2	2
9	9	2	1	22	9	1	1
10	11	1	1	23	8	1	1
11	10	2	2	24	4	2	2
12	11	2	2	25	10	1	1
13	7	2	2

Пример выполнения задания.

Пусть заданы следующие характеристики кода: k = 3, q = 2, неприводимый полином P₁ (1).

1. 
   Определим длину кода, число проверочных знаков и порождающий полином кода.
   

• 
  Поскольку код должен исправлять одиночные ошибки t = 1, то d₀  2t + 1 = 3. Обнаружения ошибок кратности 2 (q = 2) накладывает требование на значение минимального кодового расстояния d₀  2q = 4.
  
• 
  По таблице 2 (http://scask.ru/h_book_codb.php?id=20, с.69) определим необходимое число контрольных разрядов и общую длину кодовой комбинации.
  

Таблица 2 ‒ Число проверочных разрядов для заданного значения информационных разрядов k и кодового расстояния d


k = 3 и d = 3 соответствует число проверочных разрядов r = 3, для k = 3 и d = 4 ‒ r = 4.

Действительно, классический код Хемминга имеет кодовое расстояние d = 3, а повышение его кодового расстояния до значения d = 4 достигается путем добавления дополнительного контрольного разряда – бита четности.

• 
  Определим подходящий классический код Хемминга (d = 3). Этот код должен иметь число информационных разрядов не менее 3, а его общая длина должна быть не менее n  k + r = 3 + 3 = 6.
  

Поскольку число n= 6 не является числом вида 2^m – 1, то речь идет о укороченном коде Хемминга.

По таблице 3 (http://scask.ru/h_book_codb.php?id=28, стр. 93) найдем подходящий классический (n, k) код Хемминга, для которого выполняется условие n  6, k  3.

Очевидно, это будет классический (7,4) код Хемминга. Для этого кода
n = 2^m – 1 = 7, следовательно, m = log2 (7 + 1) = 3.
Таблица 3 – Коды Хемминга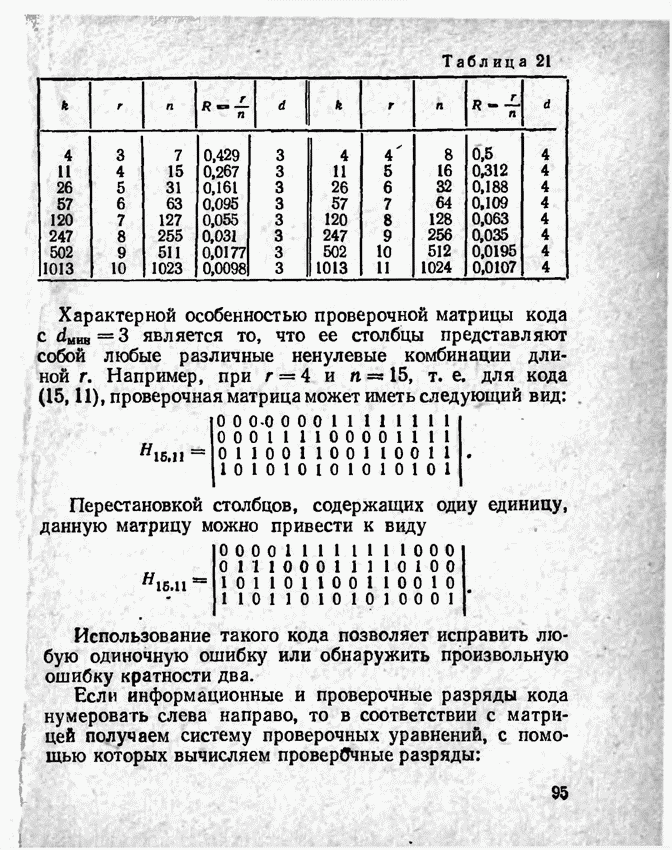


Путем вычеркивания одного информационного разряда из него может быть получен укороченный (6,3) код Хемминга. Путем добавления дополнительного проверочного разряда (кода четности) для увеличения обнаруживающей способности получим код общей длины n = 7 с тремя информационными
(k = 3) и 4 проверочными (r = 4) разрядами.

• 
  Определим порождающий полином кода Хемминга.
  

Известно, что в качестве порождающего полинома кода Хемминга выбираются примитивные неприводимые многочлены над GF(2) степени m. При этом, если какой-то многочлен неприводим (примитивен), то неприводимым (примитивным) будет и сопряженный с ним полином. Многие таблицы неприводимых полиномов из соображений компактности не содержат сопряженных полиномов (например, http://scask.ru/h_book_code.php?id=94, примитивные полиномы помечены буквами E, H, G, F). Действительно, сопряженный полином будет генерировать тот же самый код с точностью до положения контрольных разрядов. Поэтому для выбора порождающего полинома будем использовать специально сформированную таблицу 4 (таблица содержит также представления полиномов в виде двоичных – столбец 2, и восьмеричных – столбец 8, последовательностей).
Таблица 4 – Примитивные неприводимые полиномы степени m над GF(2).

Степень m	№	Примитивный полином	2	8	№	Сопряженный полином	2	8
2	1	x2 + x + 1	111	7
3	1	x3 + x + 1	1011	13	2	x3 + x2 + 1	1101	15
4	1	x4 + x + 1	10011	23	2	x4 + x3 + 1	11001	31
5	1	x5 + x2 + 1	100101	45	2	x5 + x3 + 1	101001	51
	3	x5 + x4 + x3 + x2 + 1	111101	75	4	x5 + x3 + x2 + x + 1	101111	57
	5	x5 + x4 + x2 + x + 1	110111	67	6	x5 + x4 + x3 + x + 1	111011	73

Таблице 4 соответствует следующий фрагмент таблицы неприводимых многочленов надо GF(2):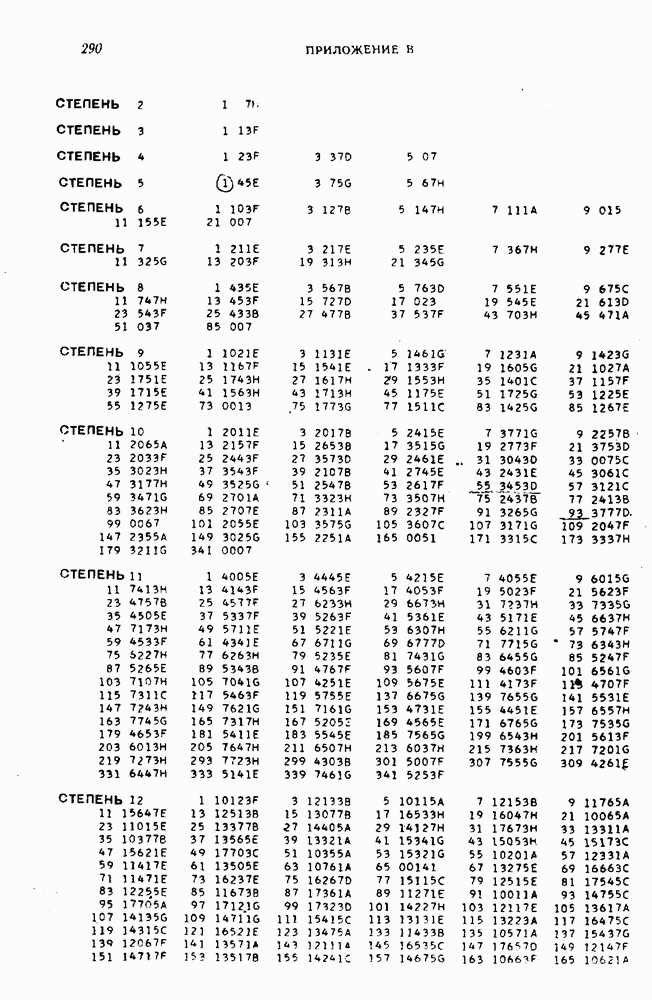


В данном случае m = 3 и, согласно заданию, требуется выбрать из таблицы первый неприводимый многочлен указанной степени – то есть
G(x) = x³ + x + 1.

Итак, имеем классический (7,4) код Хемминга с порождающим полиномом G(x) = x³ + x + 1.

2. 
   Построим производящую матрицу для выбранного классического кода Хемминга.
   

Производящая матрица кода будет иметь размер (kn) = (47). Для ее построения используем процедуру построения систематической производящей матрицы G циклического кода. Будем ее строить в виде

G = (E_k|P)

где E_k – единичная матрица размером (kk), P – матрица, строки которой получены как остатки от деления x^n-i на G(x), i = 1, …, k.

• 
  Сформируем матрицу P.
  

Рассчитаем:

x⁶ mod (x³ + x + 1) = x² + 1  101 (в двоичном виде)
x⁶ |x³ + x + 1

x⁶ + x⁴ + x³ |x³ + x + 1

x⁴ + x³

x⁴ + x² + x

x³ + x² + x

x³ + x + 1

x² + 1
x⁵ mod (x³ + x + 1) = x² + x + 1  111 (в двоичном виде)

x⁴ mod (x³ + x + 1) = x² + x  110 (в двоичном виде)

x³ mod (x³ + x + 1) = x + 1  011 (в двоичном виде)

Таким образом,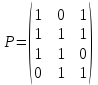

• 
  Сформируем производящую матрицу G = (E_k|P) = (E₄|P):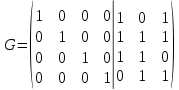
  

Проверим выполнение условия на минимальное кодовое расстояние, для этого вес каждой строки G_i производящей матрицы (то есть количество единиц в каждой строке) должен быть W(G_i)  d = 3.

Действительно, это условие выполняется: W(G₁) = 3, W(G₂) = 4, W(G₃) = 3, W(G₄) = 3.

3. 
   Из построенного классического (7,4) кода Хемминга построим укороченный (6,3) код путем вычеркивания первой строки и первого столбца матрицы G: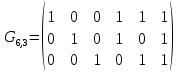
   

Эта матрица обладает той же корректирующей способностью, поскольку W(G_i)  3: W(G₁) = 4, W(G₂) = 3, W(G₃) = 3.

4. 
   Добавим дополнительный проверочный разряд – бит четности, рассчитанный как сумма над GF(2) (побитовый XOR) элементов соответствующей строки: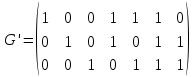
   

Удостоверимся, что полученная производящая матрица задает код с требуемым минимальным расстоянием d₀ = 4 – это действительно так, поскольку вес каждой строки W(G'_i)  4: W(G'₁) = 4, W(G'₂) = 4, W(G'₃) = 4.

Таким образом, построен код с характеристиками:

n = 7, k = 3, r = 4, d₀ = 4.

5. 
   Рассчитаем скорость V и избыточность R_n этого кода:
   

V = k/n = 3/7  0,43; R_n = 1 – V = (n – k)/n = 4/7  0,57.

6. 
   Построим проверочную матрицу кода, которая будет иметь размер rn = (47) как H' = (P'^T|E_r) = (P'^T|E₄), где G' = (E_k|P'). Для этого сначала необходимо транспонировать подматрицу P'. Это можно сделать вручную или в среде MS Excel с помощью операции Специальная вставка (установить флажок Транспонировать).
   



Тогда .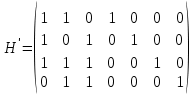

7. 
   Сформируем кодовую последовательность. Для этого выберем произвольную ненулевую кодовую комбинацию, состоящую из k = 3 информационных символов (например, 110), представим ее в виде вектор- строки I размером 1k и вычислим разрешенную кодовую комбинацию F как IG' (сложение проводится по модулю 2):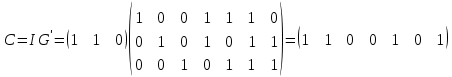
   

Для умножения матриц в MS Excel можно воспользоваться функцией массива МУМНОЖ(). Для расчета с помощью функции на листе надо выделить диапазон ячеек, по размерам совпадающий с размерами результирующей матрицы, вызвать функцию МУМНОЖ(), выбрать в качестве ее аргументов матрицы (вектор-строки, вектор-столбцы) сомножителей, а затем нажать Ctrl+Shift+Enter.

8. 
   Для этого надо вычислить синдром
   S= H'C^T (представить C как вектор-столбец):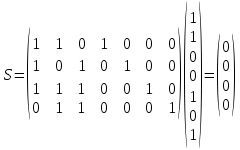
   

Получен нулевой синдром, что свидетельствует об отсутствии ошибок.

9. 
   Внесем в сформированную разрешенную кодовую комбинацию 1100101 одиночную ошибку, например, 1000101, и проверим, будет ли она обнаружена.
   

Во-первых, число единиц в этой кодовой комбинации нечетно (3), что говорит о наличии ошибки (нечетной кратности). Вычислим синдром:



Получили ненулевое значение синдрома, что также свидетельствует о наличии ошибки. В предположении, что произошла одиночная ошибка, можно определить ее позицию – для этого найти столбец проверочной матрицы H', совпадающий со значением синдрома. Это столбец 2, значит ошибка произошла во второй позиции переданной кодовой комбинации. Исправим ее:

1000101  1100101

Получили исходную (разрешенную) кодовую комбинацию.

10. 
    Внесем в разрешенную кодовую комбинацию 1100101 ошибку кратности 2, например, 0101101, и проверим, будет ли она обнаружена.
    

По биту четности ошибка не может быть обнаружена, поскольку число единиц в искаженной кодовой комбинации четно (4). Вычислим значение синдрома: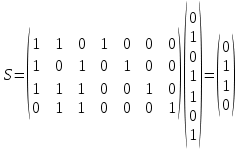



Получен ненулевой синдром, что свидетельствует о наличии ошибки. Можно также утверждать, что произошла ошибка четной кратности. Однако установить местоположение кратной ошибки невозможно.

Задание 2. Построить код Боуза-Чоудхури-Хоквингема (БЧХ) с длиной кодовой комбинации, не превышающей заданного числа байт (n), гарантированно исправляющий все ошибки кратности t.

Оценить основные информационные характеристики этого кода.

Привести пример кодирования и декодирования для указанной информационной последовательности I(x) (в полиномиальном виде) в случае отсутствия ошибки, а также пример исправления ошибки максимальной кратности t.

Параметры кода выбираются из таблицы 5 в соответствии с вариантом выполнения задания. Вариант определяется порядковым номером студента в официальном списке группы.

Таблица 5 – Варианты выполнения задания 2

вариант	n, байт	t	I(x)	вариант	n, байт	t	I(x)
1	4	3	x15+x12+x5	14	4	3	x10+x8+x6+x2
2	2	3	x2+x+1	15	4	2	x5+x2+1
3	4	3	x12+x11+x10+x2+x+1	16	2	3	x3+x2+1
4	2	2	x6+x3+1	17	4	3	x10+x9+x5+x6+1
5	2	3	x3+x	18	2	3	x4+x2+1
6	4	2	x20+x10+x	19	2	2	x5+x
7	4	3	x15+x14+x3+x2+x	20	4	3	x15+x10+x
8	2	2	x5+x4+x3+x2	21	4	2	x20+x15+x14+x8+x7
9	4	3	x15+x9+x8+x7+x2+1	22	2	2	x6+x2
10	2	3	x4+1	23	4	3	x13+x12+x6+x5+1
11	2	2	x5+x3	24	4	2	x18+x12+x6
12	2	3	x3+x2+x+1	25	2	2	x6+x4+x2+x
13	4	2	x20+x2+1

Пример выполнения задания.

Пусть заданы следующие характеристики кода: длина n блока не более 8 байтов, код гарантированно исправляет все ошибки кратностиt  2.

1. 
   Определим длину n, число информационных k и проверочных разрядов r БЧХ-кода.
   

• 
  Длина кода n ограничена сверху 8 байтами: 8·8 = 64 двоичными разрядами. БЧХ код имеет длину n = 2^m – 1, поскольку 64 = 2⁶, то m = 6, n = 63.
  

Боуз и Чоудхури показали, что для любых целых положительных чисел mи t существует циклический код значности n = 2^m – 1 с кодовым расстоянием d₀  2t + 1, исправляющий t и менее ошибок. При этом число проверочных символов r = n – k не превышает величины mt.

• 
  Определим необходимое значение d₀: d₀ ≥ 2t + 1.
  

По условию требуется исправлять все двойные ошибки, поэтому
d₀ = 2t + 1 = 2·2 + 1 = 5.

• 
  Для кода БЧХ с требуемым значением d₀ = 5 определим число информационных и проверочных разрядов по таблице 6 (http://scask.ru/h_book_codb.php?id=47, стр. 200).
  

Таблица 6 ‒ Характеристики БЧХ кодов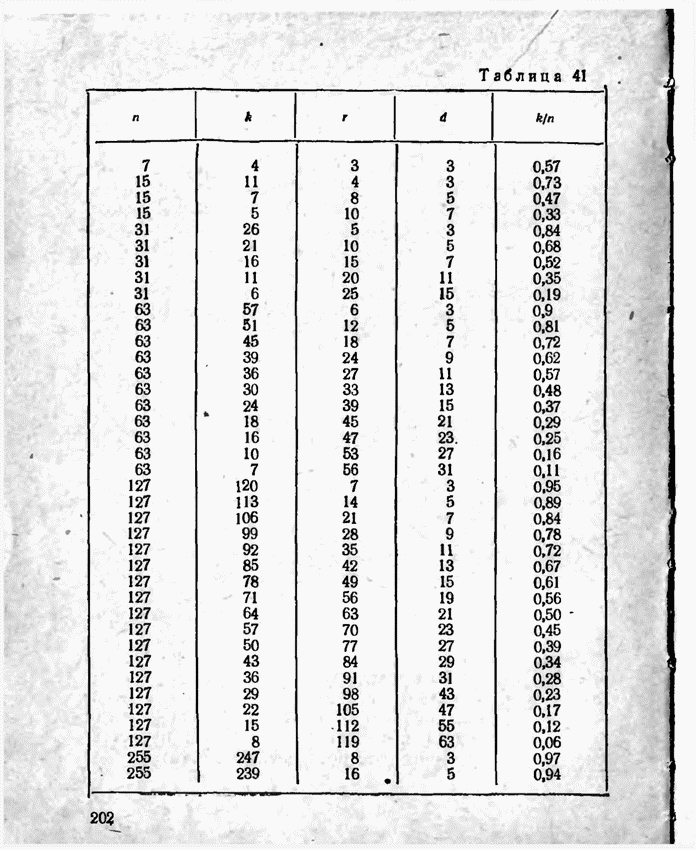


Для n = 63 и d = 5 имеем: k = 51, r = 12.

Действительно r  mt = 6·2 = 12.

2. 
   Построим порождающий полином G(x) БЧХ кода.
   

• 
  Для построения порождающего полинома БЧХ кода необходимо по значению m выбрать из таблицы неприводимых полиномов все полиномы с кратностью корней i до d₀ – 2 включительно, а затем перемножить их между собой.
  

Для этих целей можно использовать таблицу 7 (http://scask.ru/h_book_code.php?id=94, стр. 285) либо таблицу (http://scask.ru/h_book_codb.php?id=47, стр. 202).
Таблица 7 – Неприводимые многочлены над полем GF(2)



В таблице 7 кратность корня i указана перед многочленом. Полиномы записаны в виде восьмеричного числа, к которому может быть добавлена буква, указывающая на его свойства.

В рассматриваемом примере m = 6, d = 5, значит требуется выбрать все полиномы 6 степени для i = 1, 3.

Это будут полиномы 1 103F и 3 127B. Здесь числа 103 и 127 задают восьмеричное представление полиномов. Каждый разряд восьмеричной записи соответствует 3 двоичным разрядам. Переведем восьмеричную запись сначала в двоичную (ведущие нули можно опускать), а затем в полиномиальное представление:

103  1000011  x⁶ + x + 1

127  1010111  x⁶ + x⁴ +x² + x + 1

• 
  Перемножим полученные полиномы (сложение коэффициентов при одинаковых степенях производится по модулю 2):
  

G(x) = (x⁶ + x⁴ + x² + x + 1)(x⁶ + x + 1) = x¹² + x¹⁰ + x⁸ + x⁷ + x⁶ +x⁷ + x⁵ + x³ + x² + x +x⁶ + x⁴ +x² + x + 1 = x¹² + x¹⁰ + x⁸ + x⁵ + x⁴ + x³ + 1

Получили порождающий полином для (63,51) кода БЧХ с конструктивным кодовым расстоянием d₀ = 5.

3. 
   Оценим избыточность и скорость этого кода: R_n = r/n = 12/63  0,19,
   V = 1 – R_n = k/n = 51/63  0,81.
   
4. 
   Сгенерируем кодовую комбинацию БЧХ кода.
   

Поскольку построенный код слишком длинный, продемонстрируем последующие действия на примере (15,7) кода БЧХ с порождающим полиномом G(x) = x⁸ + x⁷ +x⁶ + x⁴ + 1. Этот код имеет 8 проверочных разрядов и способен исправлять ошибки кратности 2.

Можно воспользоваться стандартной процедурой построения циклического кода. Возьмем ненулевую кодовую последовательность из kсимволов (в полиномиальной записи старшая степень не превосходит k ‒ 1): в рассматриваемом примере k = 7, максимальная степень 6. Возьмем, например, I(x) = x⁶ + x.

При выполнении задания необходимо выбрать информационный полином из таблицы 5 в соответствии с номером варианта.

• 
  Сформируем контрольные разряды:
  

R(x) = P(x)·x^r mod G(x) = (x⁶ + 1)·x⁸ mod (x⁸ + x⁷ + x⁶ + x⁴ + 1) = (x¹⁴ + x⁹) mod (x⁸ + x⁷ + x⁶ + x⁴ + 1) = x⁷ + x⁴ + x³ + x + 1

Расчет:

x¹⁴ + x⁹ |x⁸ + x⁷ +x⁶ + x⁴ + 1

x¹⁴ + x¹³ +x¹² + x¹⁰ +x⁶ |x⁶ + x⁵ +x³ + x + 1

x¹³ +x¹² + x¹⁰ + x⁹+x⁶

x¹³ + x¹² +x¹¹ + x⁹ +x⁵

x¹¹ +x¹⁰ + x⁶ + x⁵

x¹¹ + x¹⁰ +x⁹ + x⁷ +x³

x⁹ + x⁷ + x⁶ + x⁵ +x³ x⁸ +x⁶ +x³ + x

x⁹ + x⁸ +x⁷+ x⁵ + xx⁸ + x⁷ +x⁶+ x⁴ + 1

x⁸ +x⁶ +x³ + xx⁷ +x⁴ +x³ + x+ 1

В двоичном виде умножение на x^r сводится к дописыванию справа r нулей к информационной комбинации, G = 111010001. Тогда, в двоичном виде получаем R = 10011011: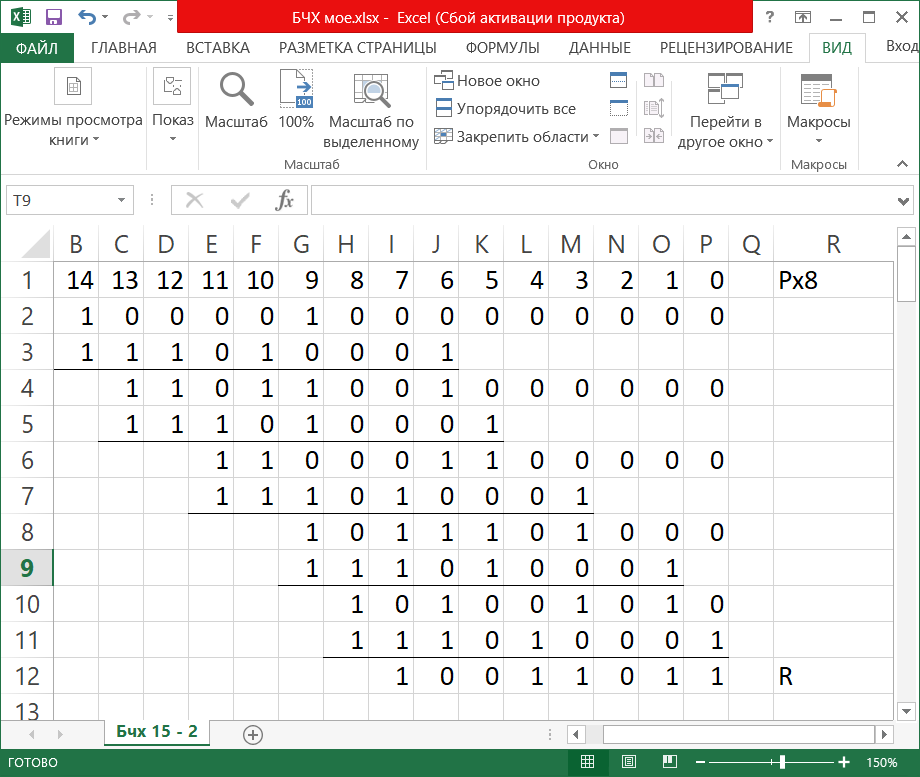

• 
  Тогда кодовая комбинация БЧХ кода имеет вид:
  

F(x) = P(x)x^r + R(x) = x¹⁴ + x⁹ + x⁷ + x⁴ + x³ + x + 1

• 
  Проверим, что эта комбинация является разрешенной. Разрешенная комбинация циклического кода делится без остатка на G(x). Действительно, F(x) mod G(x) = (x¹⁴ + x⁹ + x⁷ +x⁴ +x³ + x+ 1) mod (x⁸ + x⁷ +x⁶ + x⁴ + 1) = 0
  

x¹⁴ + x⁹ + x⁷ +x⁴ +x³ + x+ 1 |x⁸ + x⁷ +x⁶ + x⁴ + 1

x¹⁴ + x¹³ +x¹² + x¹⁰ +x⁶ |x⁶ + x⁵ +x³ + x+ 1

x¹³ +x¹² + x¹⁰+ x⁹ + x⁷ +x⁶ +x⁴ +x³ + x+ 1

x¹³ + x¹² +x¹¹ +x⁹ + x⁵

x¹¹ + x¹⁰+ x⁷ +x⁶ + x⁵ +x⁴ +x³ + x+ 1

x¹¹ + x¹⁰+ x⁹ +x⁷+ x³

x⁹ +x⁶ + x⁵ +x⁴ +x+ 1

x⁹ + x⁸ +x⁷ + x⁵ +x

x⁸ +x⁷ + x⁶ + x⁴ + 1

x⁸ + x⁷ +x⁶ + x⁴ + 1

0

или, в двоичном виде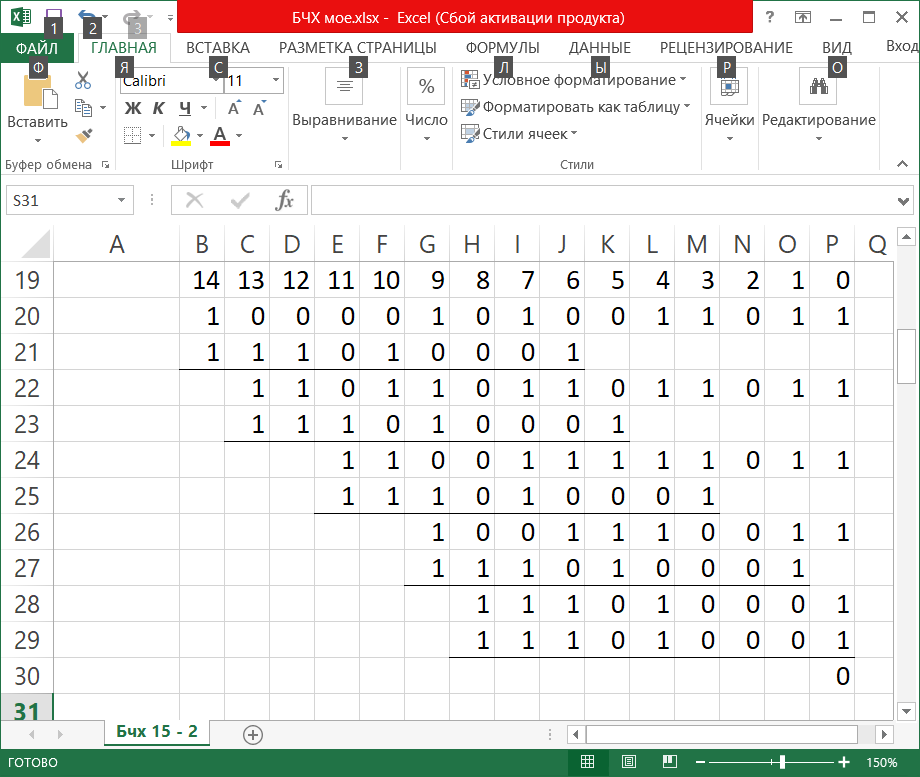

5. 
   Внесем в кодовую комбинацию ошибку максимально обнаруживаемой кратности (в данном случае 2) и проведем процедуру ее обнаружения.
   

• 
  Пусть при передаче кодовая комбинация F(x) была искажена, добавим ошибку кратности 2 (например, пропустим одну степень и добавим другую в информационных разрядах):
  

F(x) = x¹⁴ + x⁹ + x⁷ + x⁴ + x³ + x + 1 

F'(x) = x¹⁴ + x¹¹ + x⁷ + x⁴ + x³ + x + 1

При выполнении задания вносите ошибки в старшие разряды, чтобы для обнаружения ошибок потребовалось меньше шагов алгоритма.

• 
  Найдем синдром S(x) = F'(x) mod G(x) = (x¹⁴ + x¹¹ + x⁷ + x⁴ + x³ + x + 1) mod
  (x⁸ + x⁷ + x⁶ + x⁴ + 1) = x⁶ + x⁵ + x³ + x² + x  0
  

x¹⁴ + x¹¹ + x⁷ + x⁴ + x³ + x + 1 | x⁸ + x⁷ + x⁶ + x⁴ + 1

x¹⁴ + x¹³ + x¹² + x¹⁰ + x⁶ | x⁶ + x⁵ + x² + 1

x¹³ +x¹² +x¹¹ + x¹⁰ + x⁷ + x⁶ + x⁴ + x³ + x + 1

x¹³ + x¹² +x¹¹+ x⁹ + x⁵

x¹⁰ + x⁹ + x⁷ + x⁵ + x⁴ + x⁶ + x³ + x + 1

x¹⁰ + x⁹ + x⁸ + x⁶ + x²

x⁸ + x⁷ + x⁵ +x⁴ + x³ + x² + x + 1

x⁸ + x⁷ +x⁶ + x⁴ + 1

x⁶ +x⁵ +x³ +x² + x

или, в двоичном виде



Значение синдрома отлично от нуля, значит имеется ошибка.

• 
  Проведем коррекцию ошибочной комбинации в предположении наличия ошибки кратности 2.
  

Будем использовать следующий метод определения места ошибки.

1) Вычисление остатка. Принятую кодовую комбинацию F'(x) делят на G(x), и если остаток S(x) = F'(x) mod G(x) отличен от нуля, произошла ошибка.

2) Подсчет веса остатка W. Если вес остатка равен или меньше числа исправляемых ошибок, т.е. W  t, то принятую комбинацию складывают по модулю 2 с остатком и получают исправленную комбинацию.

3) Циклический сдвиг на один символ влево. Если W > t, то производят циклический сдвиг на один символ влево и полученную комбинацию снова делят на G(x).

Если вес полученного остатка W  t, то циклически сдвинутую комбинацию складывают с остатком и затем циклически сдвигают ее в обратную сторону вправо на один символ. В результате получают исправленную комбинацию.

4) Дополнительные циклические сдвиги влево. Если после циклического сдвига на один символ по-прежнему W > t, производят дополнительные циклические сдвиги влево. При этом после каждого сдвига сдвинутую комбинацию делят на G(x) и проверяют вес остатка. При W  t выполняют действия, указанные в шаге 3, с той лишь разницей, что обратных циклических сдвигов вправо делают столько, сколько их было сделано влево.

Эту процедуру удобнее выполнять в двоичном виде.

1. 
   Остаток S = 1101110 вычислен ранее.
   
2. 
   Вес полученного остатка W(S) = 5 > t = 2. Значит необходимо сделать циклический сдвиг. Для обозначения величины сдвига будем использовать переменную R.
   
3. 
   R = 1, проведем циклический сдвиг F' = 100100010011011 влево:
   F'₁ = 001000100110111. Вычислим остаток от деления на G(x):
   

S₁ = 11011100, W(S) = 5 > 2.

4. 
   R = 2, проведем циклический сдвигF'₁ = 001000100110111 влево:
   F'₂ = 010001001101110, вычислим остаток.
   

S₂ = 110111000, W(S) = 5 > 2.

5. 
   R = 3, проведем циклический сдвиг F'₂ = 010001001101110 влево:
   F'₃ = 100010011011100, вычислим остаток.
   

S₃ = 11010010, W(S) = 4 > 2.

6. 
   R = 4, проведем циклический сдвиг F'₃ = 100010011011100 влево:
   F'₄ = 000100110111001, вычислим остаток.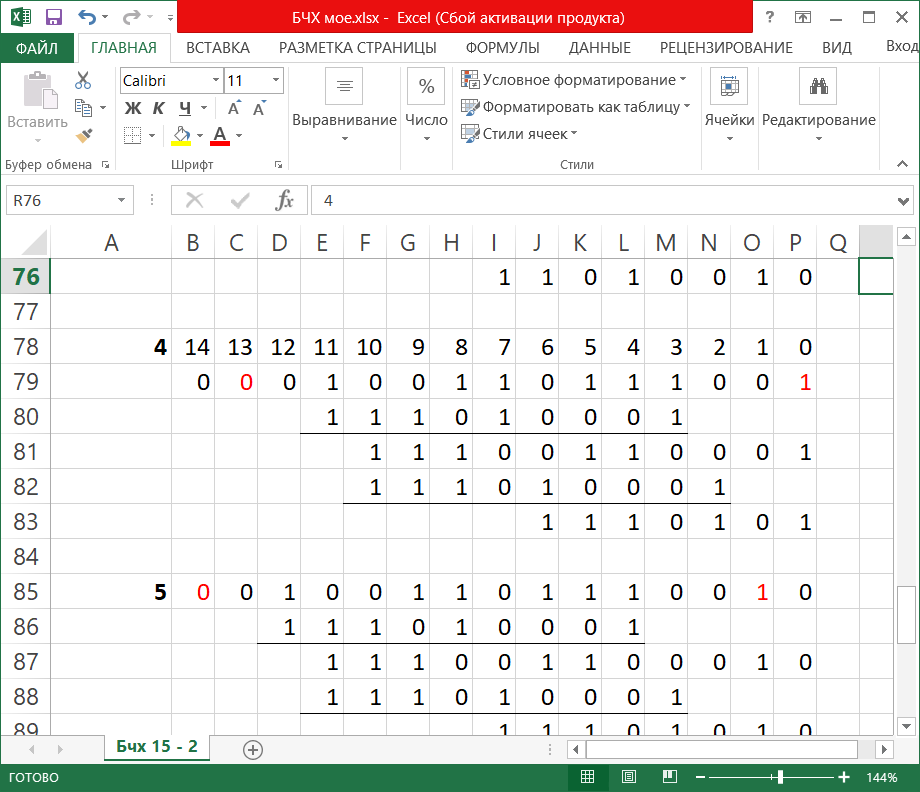
   

S₄ = 1110101, W(S) = 5 > 2.

7. 
   R = 5, проведем циклический сдвиг F'₄ = 000100110111001 влево:
   F'₅ = 001001101110010, вычислим остаток.
   

S₅ = 11101010, W(S) = 5 > 2.

8. 
   R = 6, проведем циклический сдвиг F'₅ = 001001101110010 влево:
   F'₆ = 010011011100100, вычислим остаток.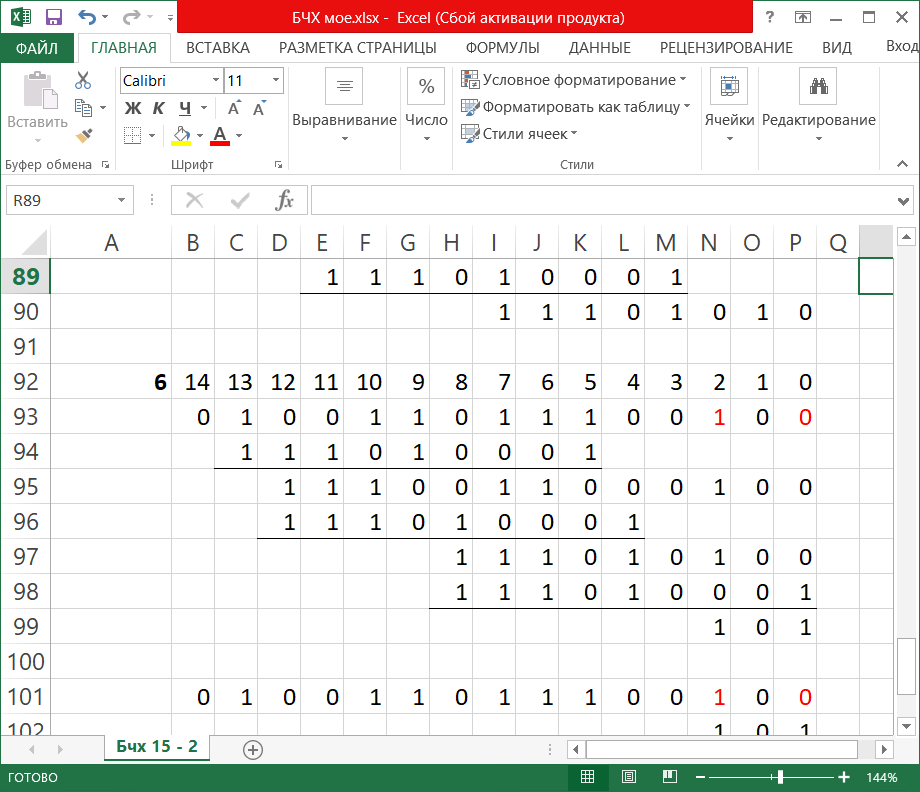
   

S₆ = 101, W(S) = 2 = t. Сложим F'₆  S₆ = 010011011100001



Полученную комбинацию циклически сдвигаем вправо (в другую сторону!) на R = 6 разрядов: F = 100001010011011.

Таким образом, получили значение 100001010011011, которое совпадает с исходной кодовой комбинацией.