геометрия. ГЕОМЕТРИЯ. Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб

• Название: Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб
• Анкор: геометрия
• Дата: 26.06.2022
• Размер: 2.7 Mb.
• Имя файла: ГЕОМЕТРИЯ.rtf
• Тип: Самостоятельная работа; #616394

Самостоятельная работа по теме 2.1.

Задание 1.

1)Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб.

параллелограмм	квадрат	прямоугольник	ромб

2)Укажите основные элементы фигур (диагонали, высоты).

3)Проверьте и напишите свойства каждой построенной фигуры

параллелограмм	квадрат	прямоугольник	ромб
Основные свойства
4 попарно равных угла, 4 попарно равных стороны, 2 диагонали, 2 высоты (к основаниям и к боковым сторонам),	4 равных прямых угла, 4 равных стороны, 2 диагонали равны и в точке пересечения образуют прямой угол.	4 равных прямых угла, 4 попарно равных стороны, 2 равные диагонали.	4 попарно равных угла, 4 равных стороны, 2 диагонали пересекаются под прямым углом, 2 высоты (к основаниям и к боковым сторонам) стороны попарно параллельны

4) Вычислите площади каждой построенной фигуры, используя различные формулы площадей (через высоту, угол между сторонами, угол между диагоналями) Ответ округлите до сотых.

5) Вычислите периметры каждой построенной фигуры

параллелограмм	квадрат	прямоугольник	ромб
Размерности
a=4 cм, b= 3 см, ha= 2 см hb= 2,6 см α= = 45° d1= 6 см, d2=3 см, = 60° Где: a; b – длины сторон, ha; hb – длины высот, α= – угол между сторонами, d1; d2 – длины диагоналей – угол между диагоналями	a=2 cм, d = 2,8 см, k=2,2 cм Где: a – длина стороны, d - длина диагонали, P – периметр, k – длина отрезка, проведенного из вершины квадрата к середине противоположной стороны	a=4 cм, b= 2 см, d = 4,5 см, = 60° Где: a; b – длины сторон, P – периметр, d - длина диагонали, – угол между диагоналями	a=2 cм, h= 1,5 см, α = 60°, d1= 3,5 см, d2=1,7 см Где: a – длина стороны, d1; d2 – длины диагоналей, d = d1 – длина меньшей диагонали, – угол между сторонами
Площадь
1) S = a• ha S = 4•2 = 8 (cм2) 2) S = b• hb S = 3•2,6 = 7,8 (cм2) 3)S = a•b•sinα S = 4•3•sin45°≈ ≈8,49(cм2) 4) S=d1•d2•sin S =•3•6• sin60°≈ ≈7,79(cм2)	1) S = a2 S = 22 = 4 (cм2) 2) S = S = ≈ ≈3,92(cм2) 3)S = S = =4 (cм2) 4) S= 4• S =4• ≈ ≈3,87(cм2)	1) S = a• b S = 4•2 = 8 (cм2) 2) S = S = = 8 (cм2) 3)S = a• S = 4•≈ ≈8,25(cм2) 4) S= S =•(4,52• sin60°)≈ ≈8,77(cм2)	1) S = a• ha S = 2•1,5 = 3 (cм2) 2) S=d1•d2 S=3,5•1,7≈ 2,98(cм2) 3) S=d2•ctg S = •1,72•ctg≈ ≈2,50(cм2) 4) S=a2•sinα S=22•sin60° ≈ ≈3,46(cм2)
Периметр
P = (a+b)•2 P = (4+3)•2 = 14 (см)	P = a•4 P = 2•4 = 8 (см)	P = (a+b)•2 P =(4+2)•2 = 12 (см)	P = a•4 P = 2•4 = 8 (см)

Задание 2.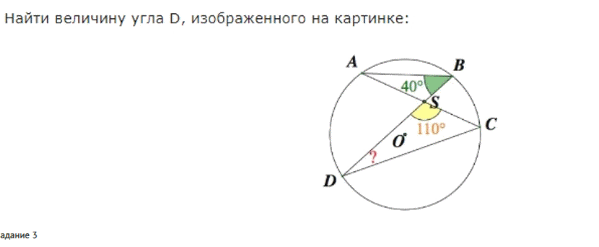



Решение

1) ABD = ACD = 40° - вписанные углы, опирающиеся на одну дугу AD.

2) В ∆DSC сумма внутренних углов равна 180°.

3) SDC = 180 – (110+40) = 30°

Ответ. D = 30°
Задание 3

В треугольнике ABC сторона AB=4 см, AС=8 см, а угол A равен 60°. Найти все стороны и все углы треугольника.

В b=4 А 60° С а=8

Дано: ∆АВС, AB=4 см, AС=8 см, A =60°. Найти: ВС, В, С

Решение

1) Найдем сторону ВС.

Из теоремы косинусов имеем:

c2=a2+b2−2ab⋅cosC

Подставим значения a,b,C в формулу выше:

c2=82+42−2⋅8⋅4⋅cos60°=48
c=4≈6.93 ВС≈6.93

2) Найдем Угол С.

Из теоремы косинусов имеем:

с2=a2+в2−2aв⋅cosС

Тогда:

cosС=(a2+в2−с2):2aв; cosС= (82+(6.928)2−42):(2⋅8⋅6.928) ≈ 0.866
∠С≈30.003°≈ 30°

3)Известны два угла треугольника. Найдем третий угол ∠В.

∠В=180°−∠А−∠C; ∠В≈180°−60°−30°≈90°

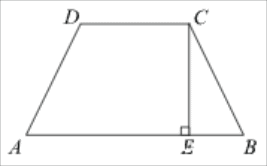
Ответ. ВС≈6.93; ∠С ≈ 30°;∠В≈90°.
Задание 4

Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.

Дано: АВСD - трапеция, AD=СB, h=8, DС = 6, tgB = 2. Найти: AB.

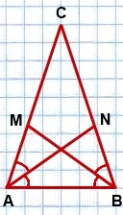
Решение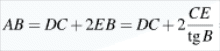





Ответ. 16.
Задание 5

Докажите, что в равнобедренном треугольнике биссектрисы, проведённые к его боковым сторонам, равны

Дано: ∆ ABC, AC=BC, AN и BM — биссектрисы.    Доказать: AN=BM.

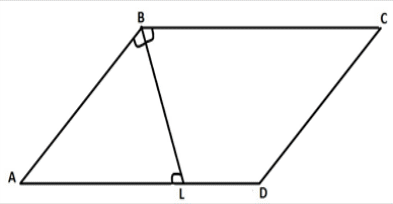
Доказательство

1. Рассмотрим треугольники ACN и BCM

1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))

2) ∠C — общий

3) ∠CAN=∠CBM (как углы, на которые биссектрисы делят равные углы при основании равнобедренного треугольника)

Следовательно, ∆ACN=∆BCM (по стороне и двум прилежащим к ней углам).

2. Из равенства треугольников следует равенство соответствующих сторон: AN=BM.

Что и требовалось доказать.
Задание 6.

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Дано: АВCD – параллелограмм, BL – биссектриса, LD:LA=3:4, P=88. Найти: AD.

Решение

1)Пусть BL - данная биссектриса.

∠ABL = ∠LBC - по условию;

∠ALB = ∠LBC - как накрест лежащие;

Значит, ∠ALB = ∠ABL. Тогда ΔABL - равнобедренный ⇒ AB = AL.

2)Пусть AD=x. Тогда



Тогда и



Зная, что P = 88, составим уравнение: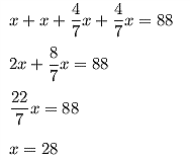



Найденная сторона будет большей.

Ответ. 28.