Самостоятельная работа2.1матем.. Задание 1 Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
Задание 1. 1)Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб. 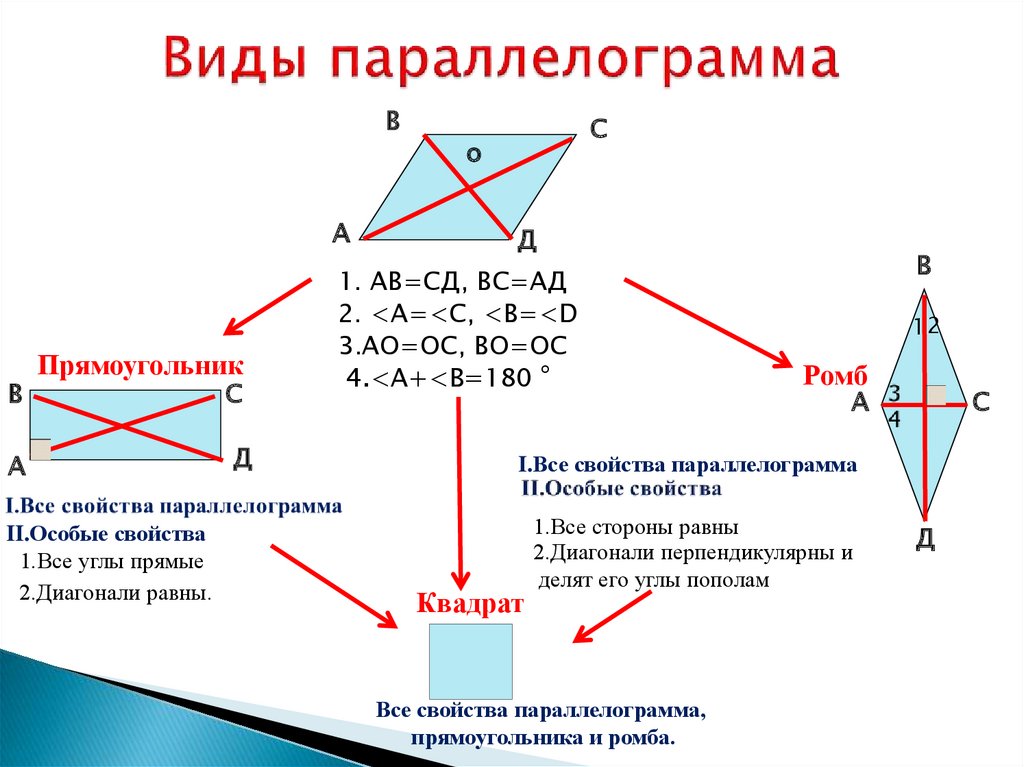 2)Укажите основные элементы фигур (диагонали, высоты). 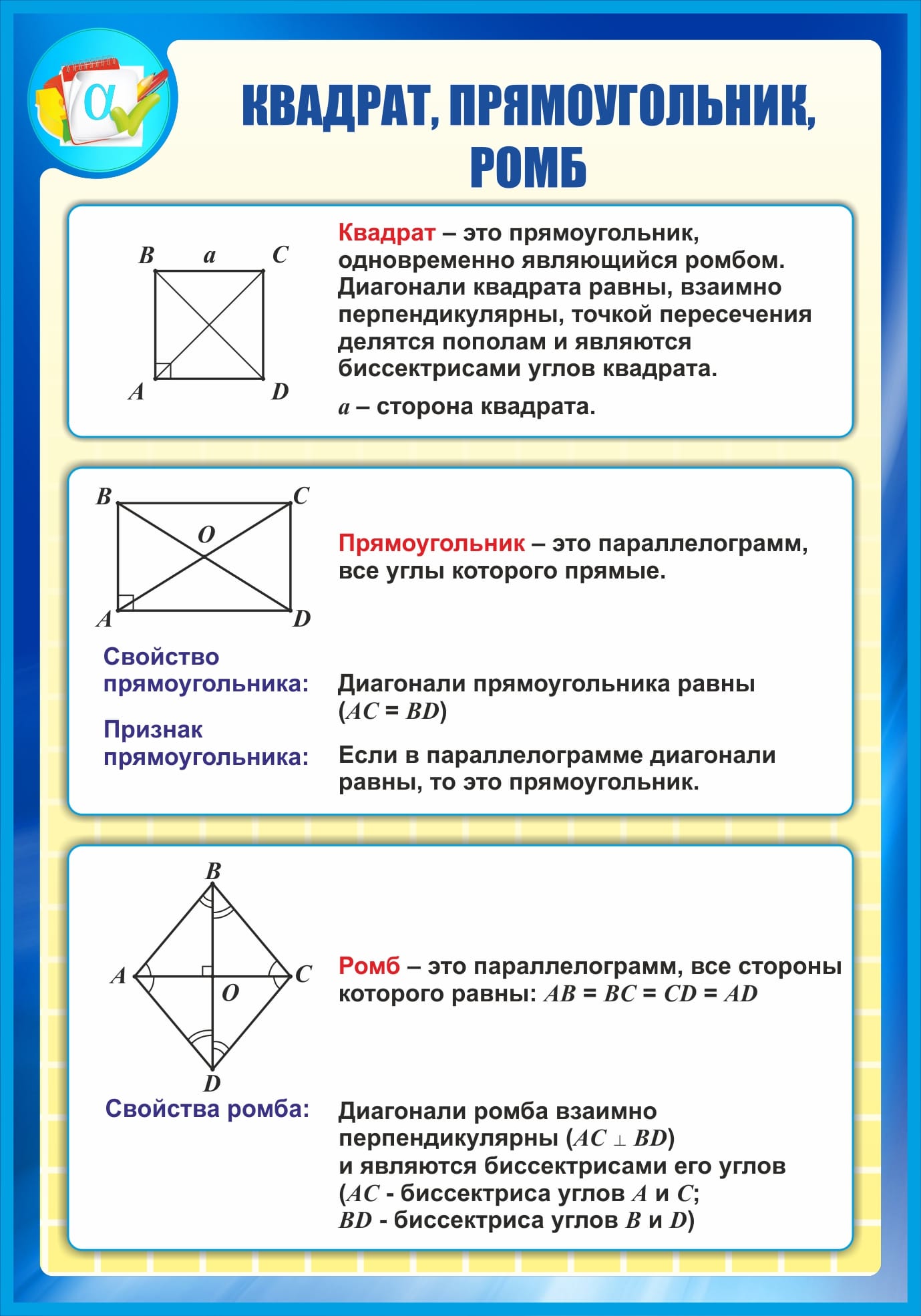 3)Проверьте и напишите свойства каждой построенной фигуры Узнать площадь прямоугольника помогут следующие формулы: S = a × b, где a, b — ширина и высота прямоугольника 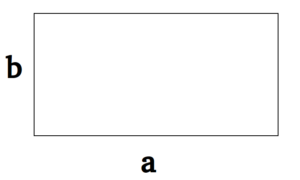 2. S = a × √(d2 - а2), где а — известная сторона, d — диагональ. 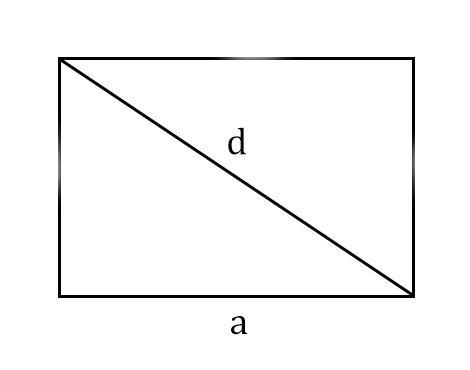 Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех. S = 0,5 × d2 × 𝑠𝑖𝑛(𝑎), где d — диагональ. 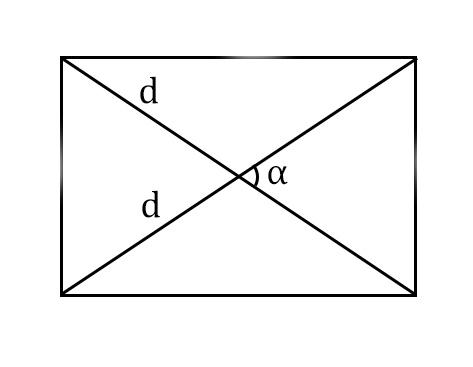 Периметр прямоугольника — сумма длины и ширины, умноженная на два. P = 2 × (a + b), где a — ширина, b — высота. 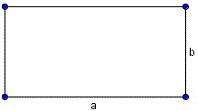 Найти площадь квадрата легко: S = а2, где a — сторона квадрата. 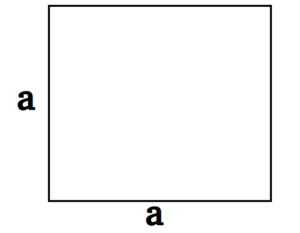 2. S = d2 : 2, где d — диагональ. 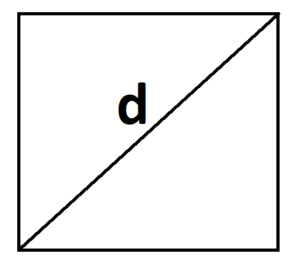 Периметр квадрата — это длина стороны, умноженная на четыре. P = 4 × a, где a — длина стороны. 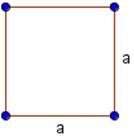 Общие формулы расчета площади фигур: S = a × h, где a — сторона, h — высота 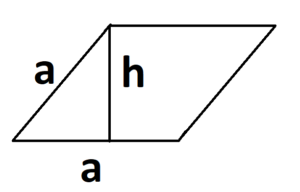 2. S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a2 × sinα. 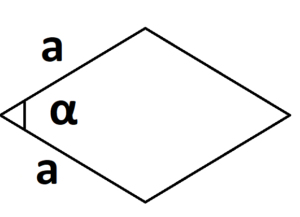 3. Для ромба: S = 0,5 × (d1 × d2), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями. 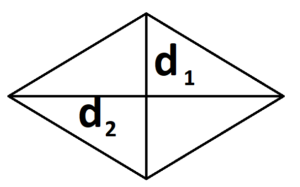 Периметр ромба — это произведение длины стороны на четыре. P = 4 × a, где a — длина стороны.  Периметр параллелограмма — сумма длины и ширины, умноженная на два. P = 2 × (a + b), где a — ширина, b — высота.  4) Вычислите площади каждой построенной фигуры, используя различные формулы площадей (через высоту, угол между сторонами, угол между диагоналями) Ответ округлите до сотых. У нас есть прямоугольник A . Одна его сторона A равна 5 см, вторая B равна 3 см. Нам нужно найти его площадь S  Чтобы найти площадь S, нужно умножить сторону A на сторону B и получаем: S = 5 ⋅ 3 Ответ: S = 15 S = 15S=15 см2. Дан прямоугольник A B C D. Его диагональ A C равна 8 см, а острый угол между диагоналями 30°. Найдите площадь фигуры.  Используем приведенную выше формулу и получаем: S = 1/2 ⋅ 8 2 ⋅ sin 30∘ = 1/2 ⋅ 64 ⋅ 1/2 = 64/4 = 16 Ответ: S=16 см2. Расчет Через сторону и высоту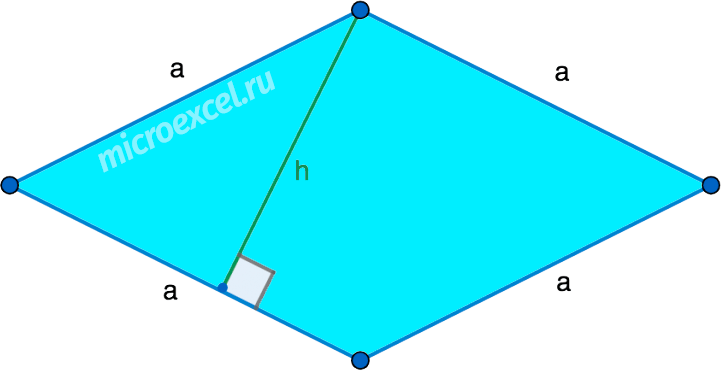 Сторона a: 8 см Высота h:10 см Площадь (S) ромба:80 см Формула расчета S = a ⋅ h 8*10=80 см Через стороны и угол между ними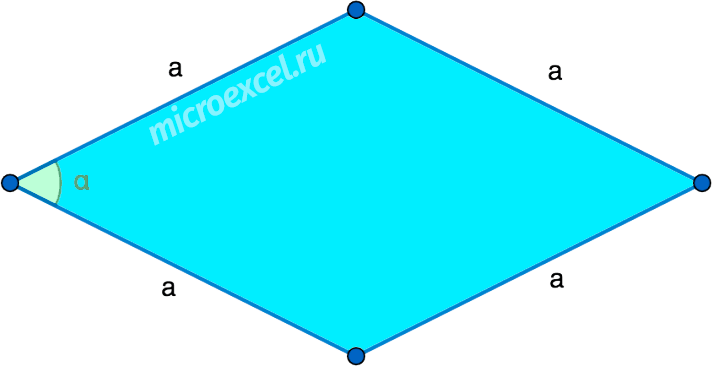 Сторона a: 8 см Угол α в (°): 30° Площадь (S) ромба: 32 см Формула расчета S = a2 ⋅ sinα 82 * sin30°=32 Через диагонали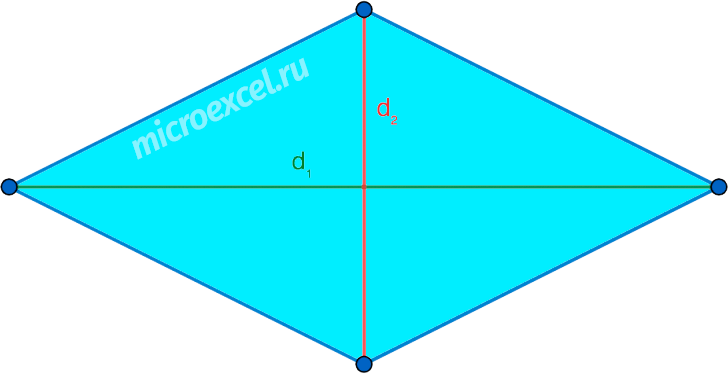 Диагональ d1: 16 см Диагональ d2: 8 см Площадь (S) ромба: 64 см Формула расчета 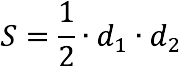 ½ * 16*8=64 5) Вычислите периметры каждой построенной фигуры | ||||||||||||||||||||||||||||||
| Решение | P = 4a = 4 · 4 = 16 |
| | |
| Ответ | P = 16 |
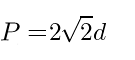
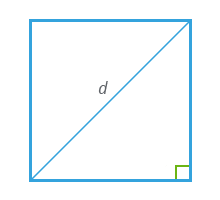
| Решение | P = 2√2d = 2 · √2 · 4 = 11,313708499 |
| | |
| Ответ | P = 11,313708499 |
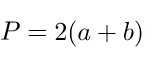

| Решение | P = 2 · (a + b) = 2 · (3 + 5) = 16 |
| | |
| Ответ | P = 16 |
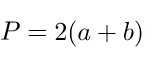
| Решение | P = 2 · (a + b) = 2 · (3 + 8) = 22 |
| | |
| Ответ | P = 22 |
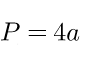
| Решение | P = 4a = 4 · 8 = 32 |
| | |
| Ответ | P = 32 |
Задание 2
Задание 3
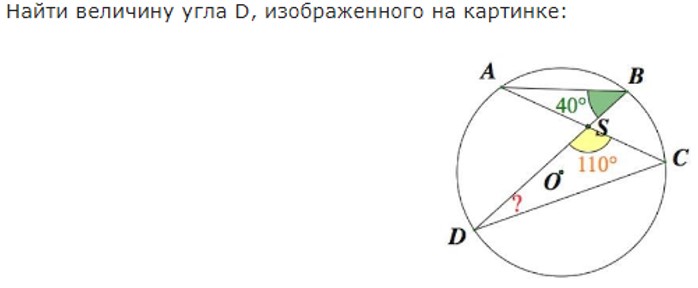
В треугольнике ABC сторона AB=4 см, AС=8 см, а угол A равен 600. Найти все стороны и все углы треугольника.
Угол ASB=DSC = 110 º, как вертикальные
Из треугольника АВС: угол DFS = = 180 º- 110 º - 40 º= 30 º.
Угол ВАС = ВDC = 30 º, так как опираются на одну и ту же дугу
Ответ: 30 º.
Задание 4
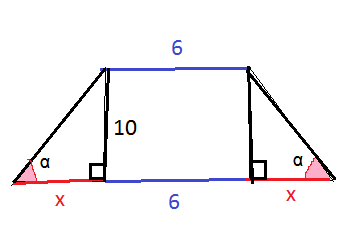
Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.
Проведем высоты из вершин верхнего основания. Получим два равных прямоугольных треугольника и прямоугольник.
tgα=10/x ( отношение противолежащего катета к прилежащему)
По условию
10/х=2
x=10:2=5
a=x+x+b=5+5+6=16
О т в е т. 16
Задание 5
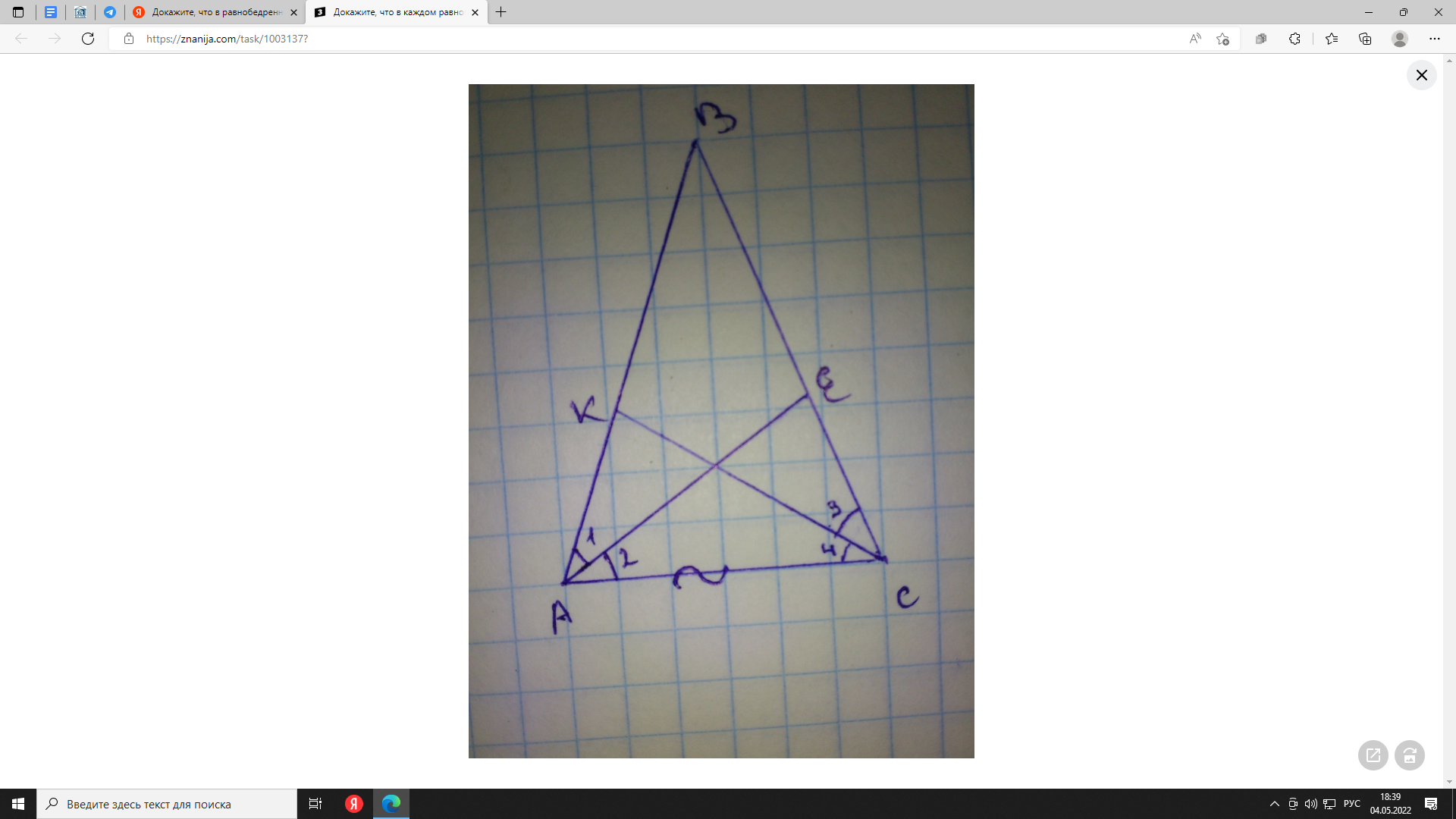
Докажите, что в равнобедренном треугольнике биссектрисы, проведенные к его боковым сторонам, равны
Треугольник АВС - равнобедренный, след-но углы при основании равны, след-во и углы 1, 2, 3, 4 раны(т.к. АЕ и СК - биссектрисы). Треуг.АКС=треуг.АЕС (угл 2=углу 4, угл ВАС = углу ВСА, сторона АС - общая) по стороне и прилежащим к ней углам, след-но КС=АЕ. :)
Задание 6.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Пусть BL - данная биссектриса.
∠ABL = ∠LBC - по условию;
∠ALB = ∠LBC - как накрест лежащие;
Значит, ∠ALB = ∠ABL. Тогда ΔABL - равнобедренный ⇒ AB = AL.
Пусть
Тогда
Тогда и
Зная, что P = 88, составим уравнение:
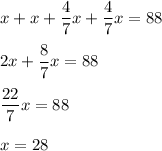
Найденная сторона будет большей.
Ответ: 28.

