Зачет по геометрии. Равнобедренный треугольник и его свойства равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Признаки равенства и подобия треугольников 1 признак

• Название: Равнобедренный треугольник и его свойства равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Признаки равенства и подобия треугольников 1 признак
• Анкор: Зачет по геометрии
• Дата: 20.06.2022
• Размер: 121.41 Kb.
• Имя файла: Зачет по геометрии.docx
• Тип: Документы; #606302

ПЛАНИМЕТРИЯ

1. 
   Равнобедренный треугольник и его свойства
   

• 
  равнобедренном треугольнике углы при основании равны.
  
• 
  В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
  

2. 
   Признаки равенства и подобия треугольников
   

1 признак: если 2 стороны одного треугольника и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2 признак: если сторона и 2 прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3 признак: если 3 стороны одного треугольника соответственно равны 3м сторонам другого треугольника, то такие треугольники равны.

1 признак. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

2 признак. Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

3 признак. Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

3. 
   Медина треугольника, свойства медианы
   

• 
  Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
  
• 
  Медиана разбивает треугольник на два равновеликих треугольника (т.е. на треугольники с одинаковой площадью).
  
• 
  Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, начиная от вершины. Эта точка называется центром тяжести треугольника.
  

4. 
   Биссектриса треугольника, свойства биссектрисы
   

• 
  Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
  
• 
  Биссектриса треугольника делит угол пополам.
  
• 
  Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
  
• 
  Точки биссектрисы угла треугольника равноудалены от сторон этого угла.
  
• 
  Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
  

5. 
   Признаки параллельности прямых
   

• 
  Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
  
• 
  Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
  
• 
  Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
  

6. 
   Прямоугольный треугольник и его свойства
   

• 
  Сумма двух острых углов прямоугольного треугольника равна 90
  
• 
  Если в прямоугольном треугольнике один из углов равен 45, то такой треугольник – равнобедренный.
  
• 
  Катет прямоугольного треугольника, лежащий против угла 30, равен половине гипотенузы
  

7. 
   Соотношения между сторонами и углами треугольника
   

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

8. 
   Параллелограмм: признаки и свойства
   

Свойства параллелограмма:

• 
  Противолежащие стороны равны.
  
• 
  Противолежащие стороны параллельны.
  
• 
  Противолежащие углы равны.
  
• 
  Сумма соседних углов равна 180.
  
• 
  Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
  
• 
  Диагональ делит пaрaллелограмм на два равных треугольника.
  
• 
  Сумма квадратов диагоналей равна сумме квадратов его четырех сторон.
  
• 
  Диагонали параллелограмма делят его на четыре равновеликих треугольника.
  

Признаки параллелограмма:

— две противолежащие стороны равны и параллельны,

— противолежащие стороны попарно равны,

— диагонали пересекаются и точкой пересечения делятся пополам,

— каждая диагональ делит четырехугольник на два равных треугольника.

9. 
   Прямоугольник, свойства:
   

• 
  Противоположные стороны прямоугольника равны и параллельны.
  
• 
  Сумма углов прямоугольника равна 360 градусов.
  
• 
  Диагонали прямоугольника имеют одинаковую длину.
  
• 
  Стороны прямоугольника являются его высотами.
  
• 
  Квадрат диагонали прямоугольника равен сумме квадратов смежных сторон прямоугольника.
  
• 
  Каждая диагональ прямоугольника делит прямоугольник на два одинаковых прямоугольных треугольника.
  
• 
  Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам.
  
• 
  Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
  
• 
  Диагональ прямоугольника является диаметром описанной окружности.
  
• 
  Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов.
  

10. 
    Ромб и квадрат, свойства.
    

• 
  Все стороны равны.
  
• 
  Все углы равны 90 градусам.
  
• 
  Диагонали квадрата равны и пересекаются под прямым углом, а точка их пересечения делит их пополам.
  

11. 
    Трапеция, виды трапеции, свойства
    

• 
  Средняя линия трапеции параллельна основаниям и равна их полусумме.
  
• 
  Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
  
• 
  Треугольники AOD и COB, образованные отрезками диагоналей и основаниями трапеции, подобны.
  
• 
  Треугольники, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
  
• 
  В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
  
• 
  Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
  
• 
  Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
  
• 
  Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
  

12. 
    Формулы площади и периметра треугольников и четырехугольников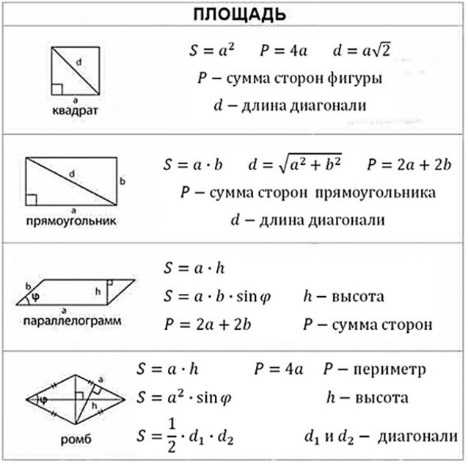
    

13. 
    Касательная к окружности, свойства касательных, угол между касательной и хордой.
    

• 
  Угол меду касательной и хордой равен половине дуги, которую стягивает данная хорда
  
• 
  Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
  
• 
  Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
  
• 
  Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
  

14. 
    Вписанный и центральный угол
    
15. 
    Вписанные и описанные окружности, их центры
    

• 
  Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
  
• 
  В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
  
• 
  Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы
  
• 
  Если сумма противоположных углов четырехугольника равна 180, то около него можно описать окружность.
  
• 
  Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
  
• 
  В четырёхугольнике центр окружности лежит на пересечении биссектрис.
  

16. 
    Формулы радиусов вписанных и описанных окружностей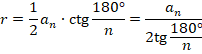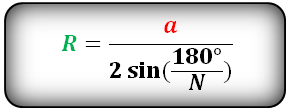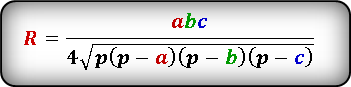
    

17. 
    Длина окружности, площадь круга, длина и площадь кругового сектора
    

СТЕРЕОМЕТРИЯ

1. 
   Параллельные прямые, признак параллельности прямых
   

• 
  Две прямые называются параллельными, если они не пересекаются и лежат в одной плоскости.
  
• 
  Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
  
• 
  Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.
  

2. 
   Параллельность прямой и плоскости, признак
   

• 
  Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
  
• 
  Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
  

3. 
   Параллельные плоскости, признак параллельности плоскостей
   

• 
  Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
  
• 
  Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
  

4. 
   Перпендикулярность прямой и плоскости, признак
   

• 
  Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
  
• 
  Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
  

5. 
   Теорема о трех перпендикулярах
   

• 
  Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.
  

6. 
   Угол между прямой и плоскостью
   

• 
  Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость.
  

7. 
   Признак перпендикулярности плоскостей
   

• 
  если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
  

8. 
   Расстояние от точки до плоскости, между скрещивающимися прямыми.
   

Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.

9. 
   Угол между плоскостями
   

• 
  Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
  

10. 
    Призма, площадь боковой и полной поверхностей, объем
    

11. 
    Пирамида, усеченная пирамида, площадь боковой и полной поверхностей, объем. Высота пирамиды.
    

12. 
    Цилиндр, сечения цилиндра, площадь боковой и полной поверхностей, объем
    

13. 
    Конус, усеченный конус, сечения, площадь боковой и полной поверхностей, объем
    

14. 
    Шар, касательная плоскость к шару, объем шара, площадь сферы
    

• 
  Касательной прямой к сфере (шару) называется прямая, имеющая со сферой единственную общую точку.
  

15. 
    Части шара и их объемы
    

• 
  Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Площадь боковой поверхности шарового сегмента:
  
• 
  Объём шарового сегмента:
  
• 
  Шаровым сектором называется тело, которое получается из шарового сегмента и конуса, основанием которого является сечение плоскостью данного шара.
  
• 
  Площадь боковой поверхности шарового сектора:
  
• 
  Объём шарового сектора:
  

16. 
    Вектор, равные вектора, коллинеарные вектора, компланарные вектора.
    

• 
  Два отличных от нуля вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. При этом два коллинеарных вектора могут быть сонаправленными или противоположно направленными.
  
• 
  Векторы называются равными, если они одинаково направлены и их длины равны.
  
• 
  Векторы, лежащие в параллельных плоскостях (или в одной плоскости), называются компланарными.
  

17. 
    Координаты вектора, длина вектора(отрезка), действия с векторами, скалярное произведение векторов
    

• 
  
  
• 
  Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. .
  

18. 
    Вычисление углов между прямыми, уравнение плоскости, расстояние от точки до плоскости.