Разработка компилятора модельного языка. Отчет. Пояснительная записка гоу огу 230105. 60. 11. 06 O руководитель работы Ишакова Е. Н. " " 2011г. Исполнитель

• Название: Пояснительная записка гоу огу 230105. 60. 11. 06 O руководитель работы Ишакова Е. Н. " " 2011г. Исполнитель
• Анкор: Разработка компилятора модельного языка
• Дата: 04.10.2020
• Размер: 1.59 Mb.
• Имя файла: Отчет.doc
• Тип: Пояснительная записка; #140979
• страница: 2 из 8

Цепочка, которая не содержит ни одного символа, называется пустой цепочкой и обозначается .

Формальное определение цепочки символов в алфавите V:

1. 
    - цепочка в алфавите V;
   
2. 
   если - цепочка в алфавитеV и а – символ этого алфавита, то  а – цепочка в алфавите V;
   
3. 
    - цепочка в алфавите V тогда и только тогда, когда она является таковой в силу утверждений 1) и 2).
   

Длиной цепочки  называется число составляющих ее символов (обозначается ||).

Конкатенацией (сцеплением) цепочек и  называется цепочка =, в которой символы данных цепочек записаны друг за другом.

Для любой цепочки справедливо утверждение =.

Степенью n цепочки  называется конкатенация n цепочек  (обозначается: ⁿ).

Для любой цепочки справедливы утверждения ⁰= иⁿ=^n-1=^n-1 для n1.

Реверсом (обращением) цепочки  называется цепочка ^R,составленная из символов цепочки , записанных в обратном порядке.

Пример 1. Пусть алфавит V={a, b, c, d}, тогда для цепочек этого алфавита =abи =bcdбудет справедливо ||=2, ||=3, =abbcd, ²=abab, ^R=dcb.

Обозначим через V^* множество, содержащее все цепочки в алфавите V, включая пустую цепочку , а через V⁺ - множество, содержащее все цепочки в алфавите V, исключая пустую цепочку .

Формальным языком L в алфавите V называют некоторое подмножество множества V^*.

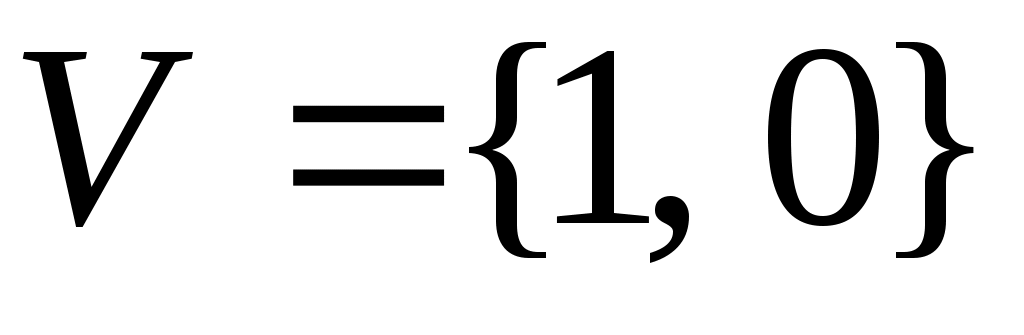
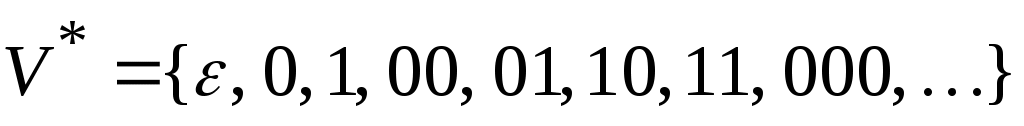
Пример 2. Пусть задан алфавит двоичных цифр , тогда , а .

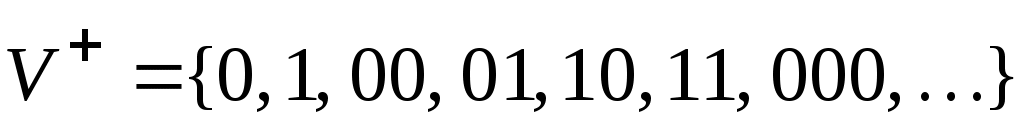
Задать язык L в алфавите V можно тремя способами:

1. 
   перечислением всех допустимых цепочек языка (на языке множеств);
   
2. 
   указанием способа порождения (генерации) цепочек языка (грамматики, формы Бэкуса-Наура и диаграммы Вирта);
   
3. 
   определением метода распознавания цепочек языка (распознаватели).
   

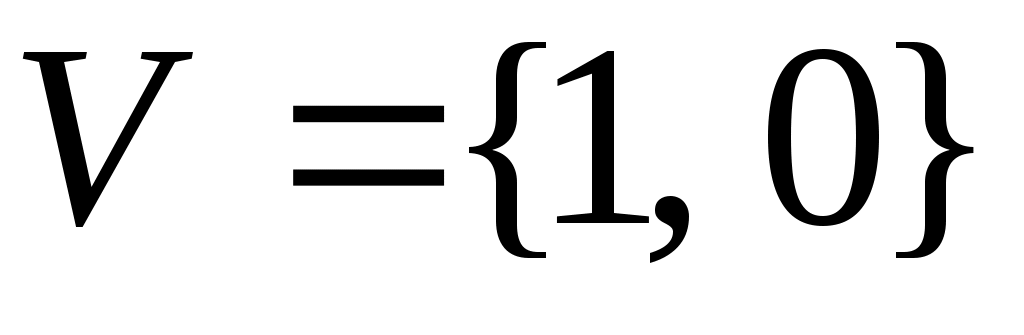
Пример 3. Язык Lв алфавите , состоящий из пустой строки и всевозможных строк, каждая из которых содержит строку нулей и последующую строку единиц той же длины, можно описать с помощью формальной системы определения множеств как L={0ⁿ1ⁿ | n0}.

Формальная грамматика – это математическая система, определяющая язык посредством порождающих правил.

Формальной грамматикой называется четверка вида:
,
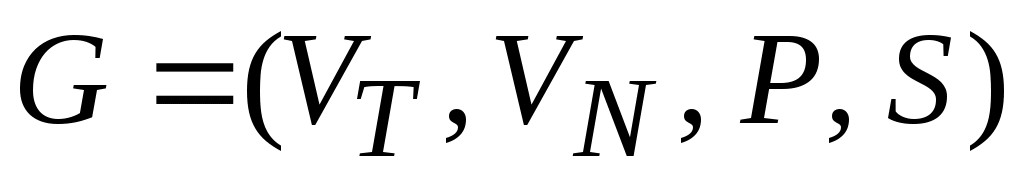
где V_N- конечное множество нетерминальных символов грамматики (обычно прописные латинские буквы);

V_T - множество терминальных символов грамматики (обычно строчные латинские буквы, цифры и т.п.),V_T V_N =;

Р - множество правил вывода грамматики, являющееся конечным подмножеством множества (V_T V_N)⁺ (V_T V_N)^*; элемент (, ) множества Р называется правилом вывода и записывается в виде (читается: «из цепочки  выводится цепочка »);

S - начальный символ грамматики, S V_N.

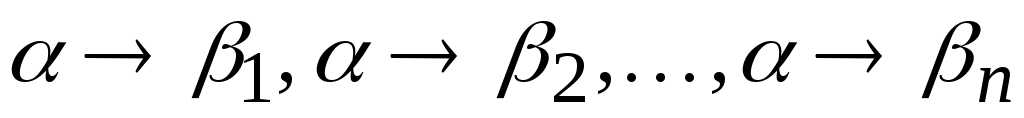
Для записи правил вывода с одинаковыми левыми частями вида используется сокращенная форма записи .

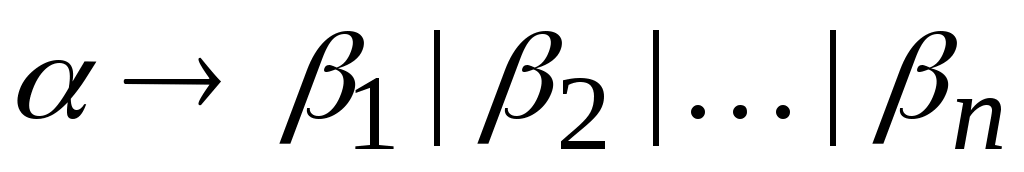
Грамматика G₁=({0, 1}, {A,S}, P₁, S), где множество Р состоит из правил вида: 1) S0A1; 2)0A00A1;3)A .

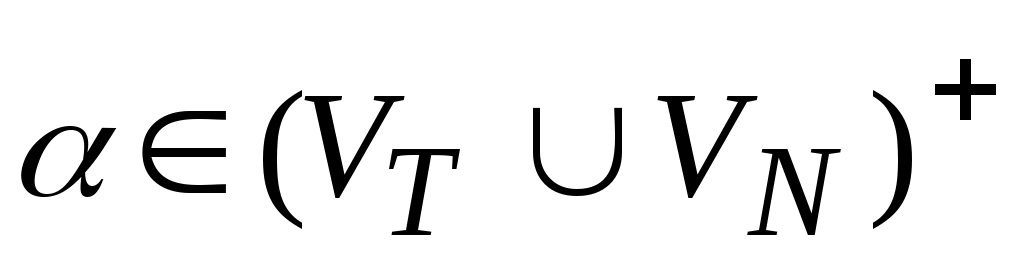
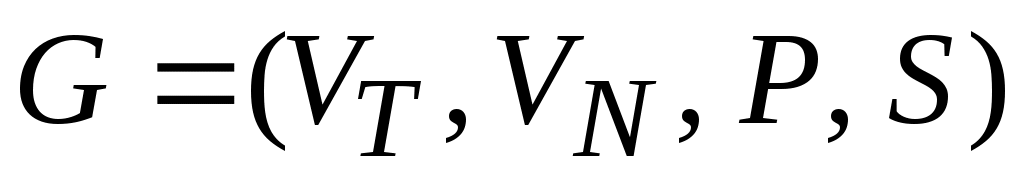
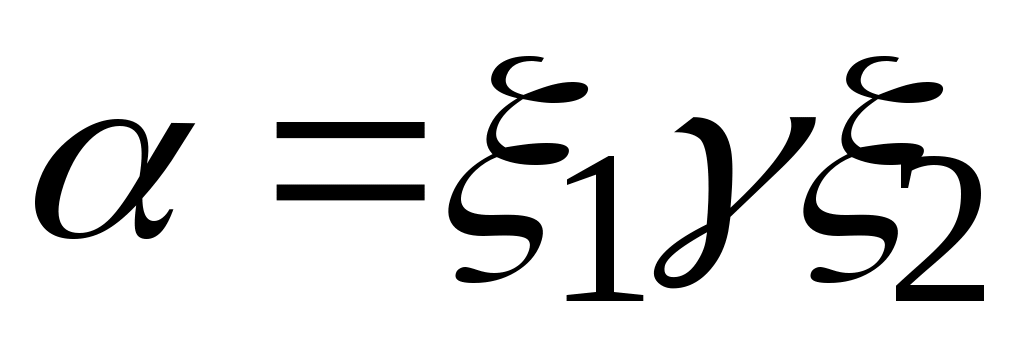
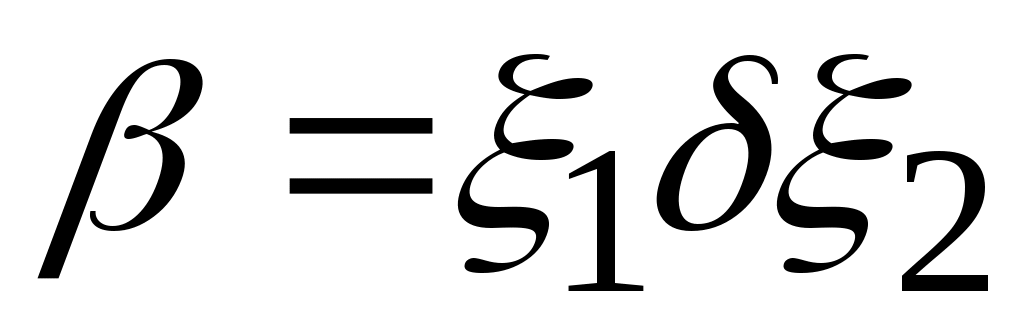
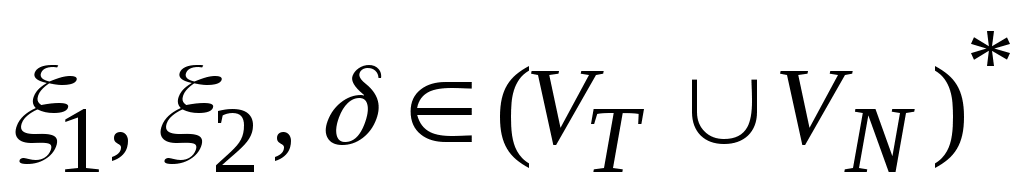
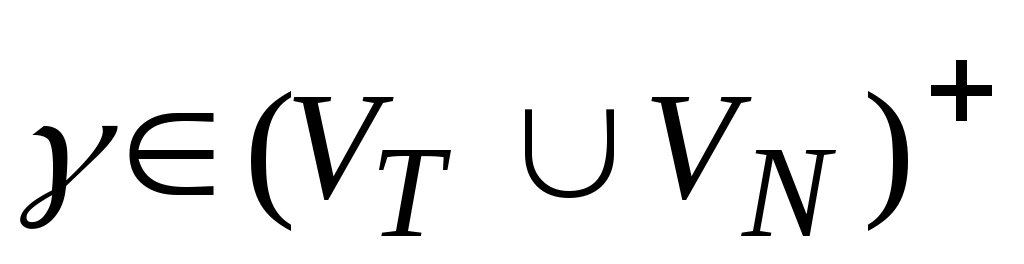
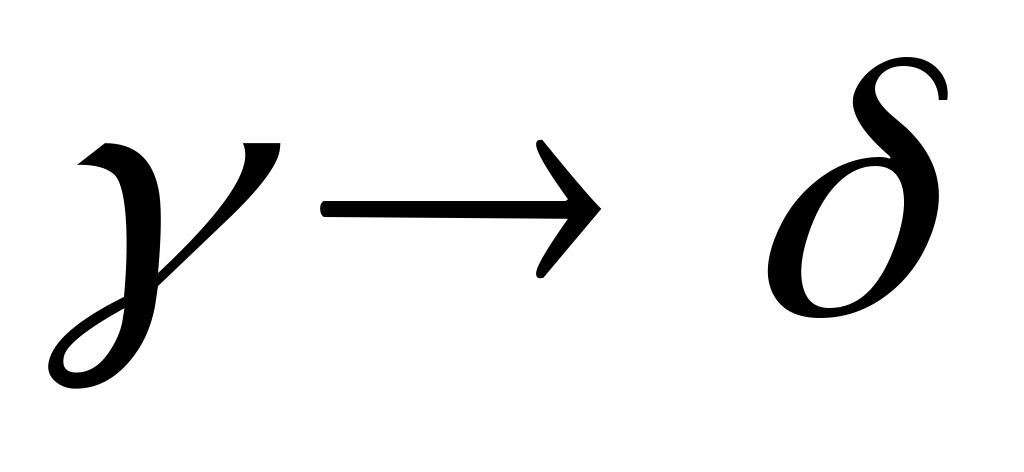
Цепочка (V_TV_N)^* непосредственно выводима из цепочки в грамматике (обозначается: ), если и , где , и правило вывода содержится во множестве Р.

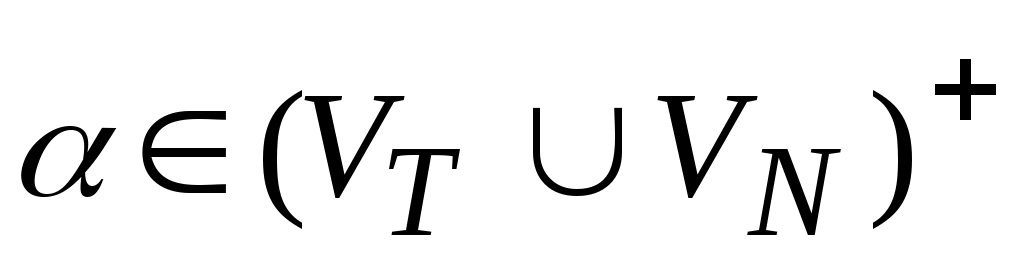
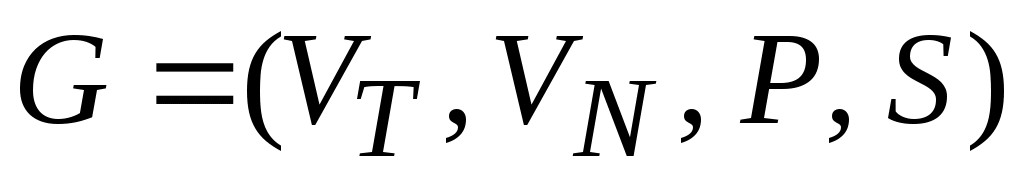
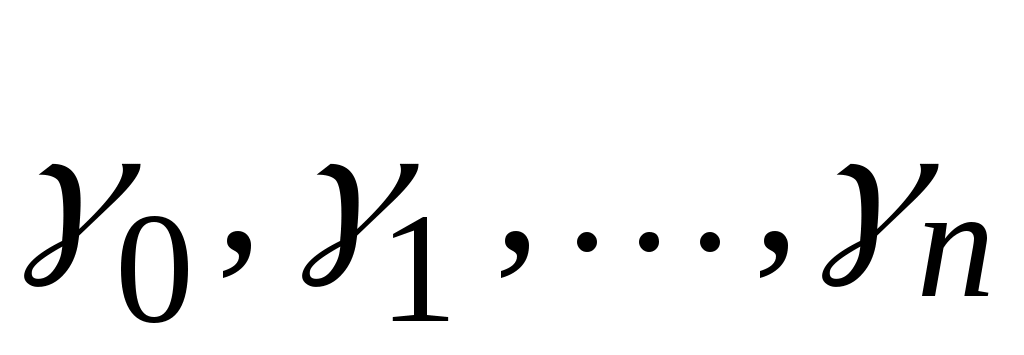
Цепочка (V_TV_N)^* выводима из цепочки в грамматике (обозначается *), если существует последовательность цепочек (n0) такая, что .

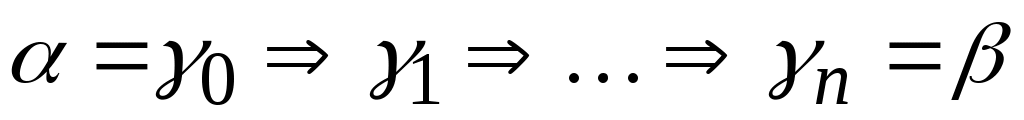
В грамматике G₁ S*000111, т.к. существует вывод S0A100A11000A111000111.

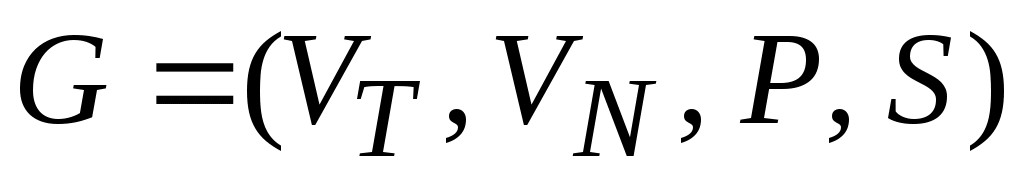
Языком, порожденным грамматикой , называется множество всех цепочек в алфавите V_T, которые выводимы из начального символа грамматики S c помощью правил множества Р, т.е. множество .

Для грамматики G₁ язык L(G₁)={0ⁿ1ⁿ | n>0}.

Цепочка 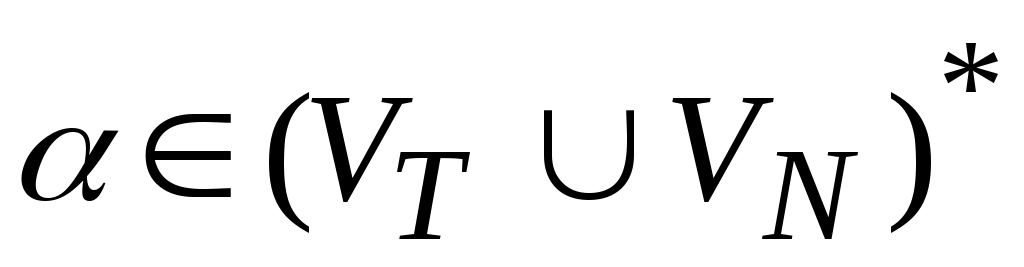, для которой существует вывод S*, называется сентенциальной формой или сентенцией в грамматике .

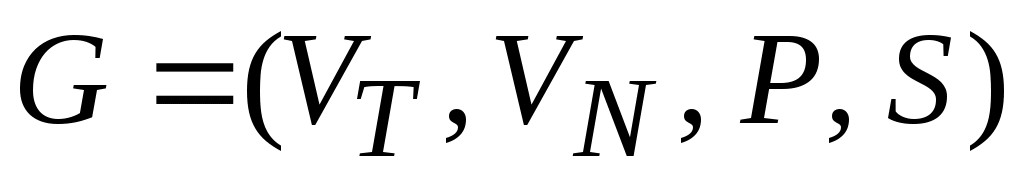Языком, порожденным грамматикой G называется множество терминальных сентенциальных форм грамматики.

Классификация грамматик в иерархии американского математика Хомского осуществляется по структуре правил вывода. В расширенной иерархии Хомского выделяется четыре типа грамматик.

Тип 0. Грамматика 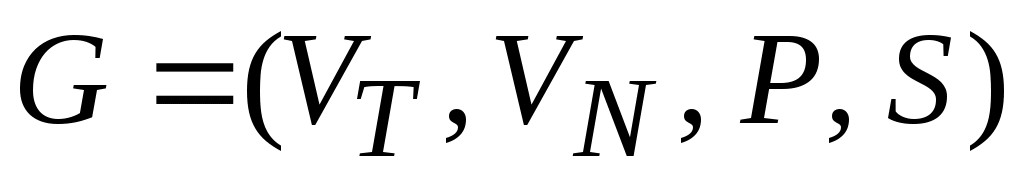называется грамматикой типа 0 (грамматикой без ограничений или грамматикой с фразовой структурой), если на ее правила вывода не наложено никаких ограничений, кроме тех, которые указаны в определении грамматики.

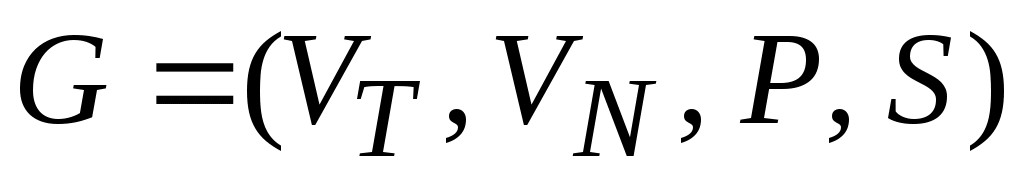
Тип 1. Грамматика называется контекстно-зависимой грамматикой (КЗ-грамматикой), если каждое правило вывода из множества Р имеет вид , где  (V_T  V_N)⁺,   (V_T  V_N)^* и ||  ||. Расширение допускает не более одного -правила, т.е. правила вида А, АV_N.

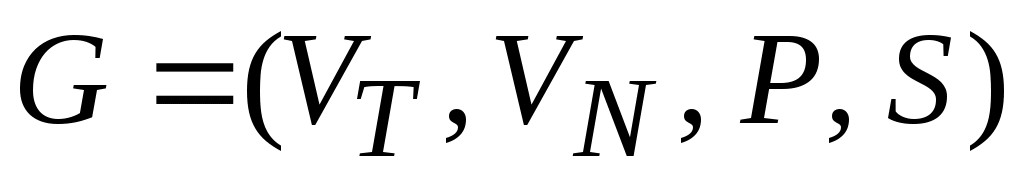
Тип 2. Грамматика называется контекстно-свободной грамматикой (КС-грамматикой), если ее правила вывода имеют вид: , где и

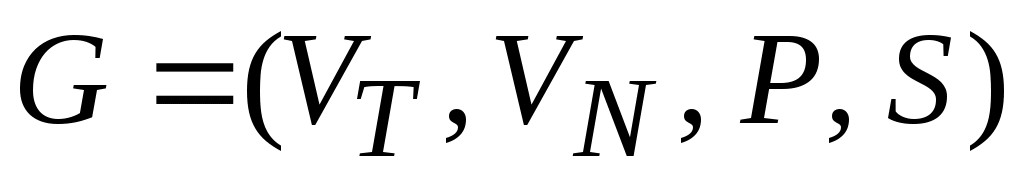
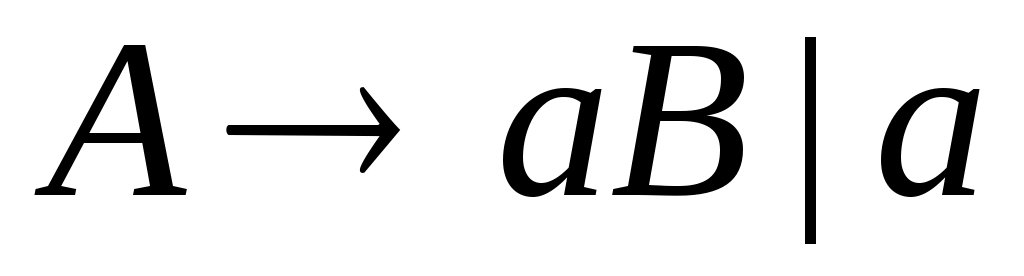
Тип 3. Грамматика называется регулярной грамматикой (Р-грамматикой) выровненной вправо, если ее правила вывода имеют вид , где .

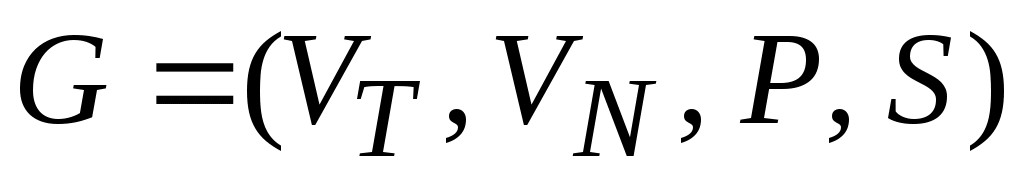
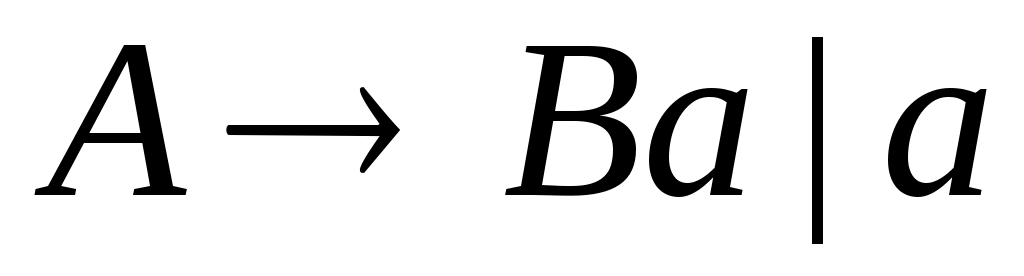
Грамматика называется регулярной грамматикой (Р-грамматикой) выровненной влево, если ее правила вывода имеют вид , где .

Расширение допускает единственное -правило вида S, но в этом случае начальный символ грамматики S не должен встречаться в правых частях правил.

Язык L(G) называется языком типа k, если его можно описать грамматикой типа k, где k – максимально возможный номер типа грамматики.

Язык вида L={0ⁿ1ⁿ | n>0} порождается КЗ-грамматикой (тип 1) G₁ (пример 1.4) и КС-грамматикой (тип 2) G₂= ({0, 1}, {S}, P₂, S), где

множество правил вывода P₂ содержит правила вида S 0S1|01.

Так как не существует регулярной грамматики (тип 3), порождающей данный язык, то язык L является языком типа 2 или КС-языком.

Примеры различных типов формальных языков и грамматик по классификации Хомского. Терминалы будем обозначать строчными символами, нетерминалы – прописными буквами, начальный символ грамматики – S.

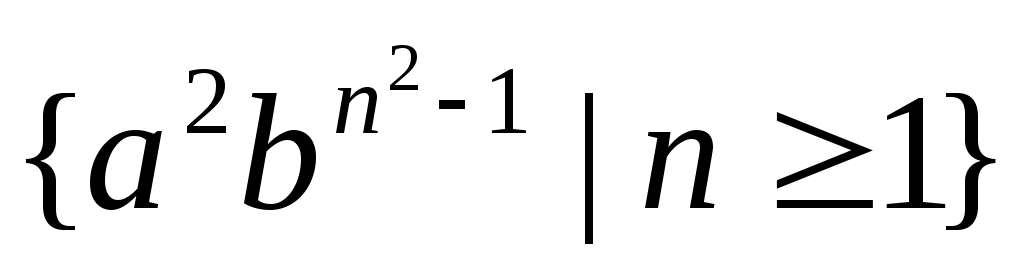
а) Язык типа 0 L(G)= определяется грамматикой с правилами вывода:

1) S  aaCFD; 2) AD  D;

3) F  AFB | AB;4) Cb  bC;

5) AB  bBA;6) CB  C;

7) Ab  bA;8) bCD  .

б) Контекстно-зависимый язык L(G)={aⁿbⁿcⁿ | n1} определяется грамматикой с правилами вывода:

1) S  aSBC | aBC;2) CB  BC;

3) aB  ab; 4) bB  bb;

5) bC  bc;6) cC  cc.

в) Контекстно-свободный язык L(G)={(aс)ⁿ(cb)ⁿ | n>0} определяется грамматикой с правилами вывода:

1) S  aQb | accb;

2) Q  cSc.

г) Регулярный язык L(G)={ | {a, b}⁺, где нет двух рядом стоящих а} определяется грамматикой с правилами вывода:

1) S  A | B;

2) A  a | Ba;

3) B  b | Bb | Ab.

Грамматики G₁ и G₂ называются эквивалентными, если они определяют один и тот же язык, т.е. .

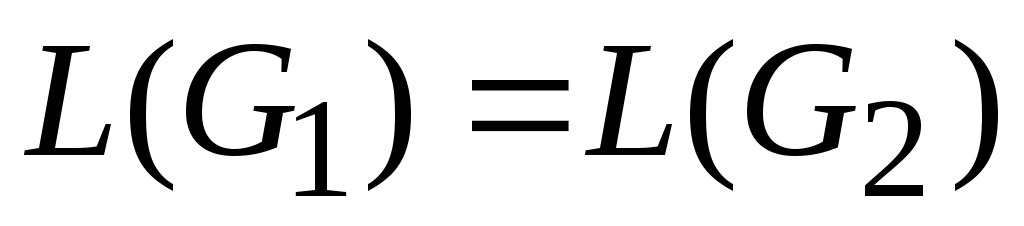
Грамматики G₁ и G₂ называются почти эквивалентными, если заданные ими языки различаются не более чем на пустую цепочку символов, т.е. .

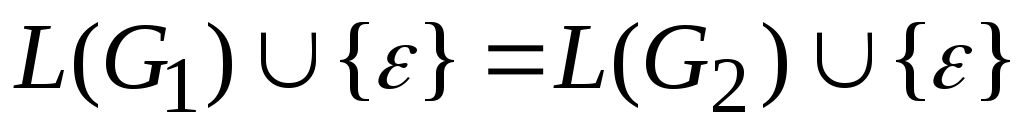
Для грамматики G₁ эквивалентной будет грамматика G₂ = ({0, 1}, {S}, P₃, S), где P₂: S 0S1|01, т.к. L(G₁)=L(G₂)={0ⁿ1ⁿ | n>0} (пример 1.7).

Почти эквивалентной для грамматики G₁ будет грамматика G₃ = ({0, 1}, {S}, P₃, S), где множество правил вывода P₃ содержит правила вида S  0S1 | , т.к. L(G₃)= {0ⁿ1ⁿ | n0}.

Цепочки языка могут содержать метасимволы, имеющие особое назначение. Метаязык, предложенный Бэкусом и Науром (БНФ) использует следующие обозначения:

• 
  символ «::=» отделяет левую часть правила от правой (читается: «определяется как»);
  
• 
  нетерминалы обозначаются произвольной символьной строкой, заключенной в угловые скобки «<» и «>»;
  
• 
  терминалы - это символы, используемые в описываемом языке;
  
• 
  правило может определять порождение нескольких альтернативных цепочек, отделяемых друг от друга символом вертикальной черты «|» (читается: «или»).
  

Для повышения удобства и компактности описаний, в расширенных БНФ вводятся следующие дополнительные конструкции (метасимволы):

• 
  квадратные скобки «[» и «]» означают, что заключенная в них синтаксическая конструкция может отсутствовать;
  
• 
  фигурные скобки «{» и «}» означают повторение заключенной в них синтаксической конструкции ноль или более раз;
  
• 
  сочетание фигурных скобок и косой черты «{/» и «/}» используется для обозначения повторения один и более раз;
  
• 
  круглые скобки «(» и «)» используются для ограничения альтернативных конструкций;
  
• 
  кавычки используются в тех случаях, когда один из метасимволов нужно включить в цепочку обычным образом.
  

В метаязыке диаграмм Вирта используются графические примитивы.

При построении диаграмм учитывают следующие правила:

• 
  каждый графический элемент, соответствующий терминалу или нетерминалу, имеет по одному входу и выходу, которые обычно изображаются на противоположных сторонах;
  
• 
  каждому правилу соответствует своя графическая диаграмма, на которой терминалы и нетерминалы соединяются посредством дуг;
  
• 
  альтернативы в правилах задаются ветвлением дуг, а итерации - их слиянием;
  
• 
  должна быть одна входная дуга (располагается обычно слева или сверху), задающая начало правила и помеченная именем определяемого нетерминала, и одна выходная, задающая его конец (обычно располагается справа или снизу);
  
• 
  стрелки на дугах диаграмм обычно не ставятся, а направления связей отслеживаются движением от начальной дуги в соответствии с плавными изгибами промежуточных дуг и ветвлений.
  

2.1 Расширенные Формы Бэкуса – Наура
Пусть синтаксис модельного языка программирования М задан с помощью РБНФ следующим образом.