Пояснительная записка Группа 2220 Студент Капинос А. С. Руководитель проекта Сенчурин Л. П. СанктПетербург 2017 Содержание
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
Санкт-Петербургский государственный морской технический университет (СПБГМТУ) Кафедра «Деталей машин и подъёмно-транспортных механизмов» ЗАЖИМ ГОРИЗОНТАЛЬНЫЙ ДВУХСТОЕЧНЫЙ Пояснительная записка Группа 2220 Студент: Капинос А.С. Руководитель проекта: Сенчурин Л.П. Санкт-Петербург 2017 Содержание 1. Расчет винта 1.1 Определение среднего диаметра резьбы винта d2 1.2 Определение внутреннего диаметра резьбы d1 1.3 Выбор cтандартных параметров резьбы 1.4 Проверка выполнения условия самоторможения в резьбе 1.5 Определение момента сил трения в резьбе 1.6 Момент сил трения на пяте винта 1.7 Проверка условия прочности на смятие в пяте винта 1.8 Определение длины рукоятки из условия равновесия моментов на винте 1.9 Определение диаметра рукоятки 1.10 Проверочный расчет винта 2. Расчет гайки 2.1 Определение высоты гайки 2.2 Проверка выполнения условия по числу витков в гайке 2.3 Определение наружного диаметра гайки 2.4 Определение диаметра бурта 2.5 Определение высоты бурта 3. КПД механизма 6.1 КПД резьбы 6.2 КПД зажима 4. Расчет корпуса механизма 5. Расчет сварных швов 6. Расчет болтовых соединений 7. Список литературы 1. Расчет винта 1.1 Определение среднего диаметра резьбы винта d2 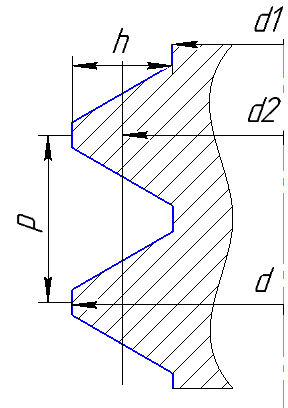 Рисунок 1 – Схема резьбы болта Определяется из условия износостойкости витков резьбы Условие имеет вид: 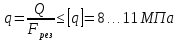 Отсюда получаем формулу для d2 проектировочного расчета: 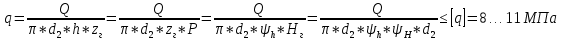 Где: 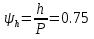 , ,  = 1.5…2.5. = 1.5…2.5.Отсюда формула: 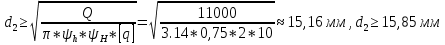 1.2 Определение внутреннего диаметра резьбы d1 Определяется из условия устойчивости винта от действия осевой продольной силы Q:  Критическое напряжение σкр зависит от гибкости винта:  , где µ- параметр заделки концов винта, i – радиус инерции, l-длина , где µ- параметр заделки концов винта, i – радиус инерции, l-длина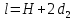 , , 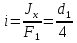 , , 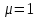 Задача решается методом последовательных приближений. Задается 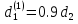 в первом приближении и подставляется в формулы. Проверяется условие устойчивости в первом приближении. Если условие не было выполнено, то переходят ко второму приближению d1(2)=1.2d1(1), снова повторяется весь цикл расчетов по второму приближению с проверкой условия устойчивости. в первом приближении и подставляется в формулы. Проверяется условие устойчивости в первом приближении. Если условие не было выполнено, то переходят ко второму приближению d1(2)=1.2d1(1), снова повторяется весь цикл расчетов по второму приближению с проверкой условия устойчивости.Если λ˃90 , то винт гибкий: 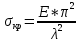 (по формуле Эйлера). (по формуле Эйлера).Если 40 ≤ λ ≤ 90, то винт жесткий: 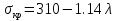 (по формуле Ясинского). (по формуле Ясинского).Если λ ˂ 40, то проверка на устойчивость не требуется. 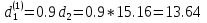 мм мм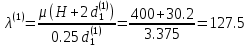 Так как  , то , то  =121.3 МПа =121.3 МПаПроверка условия устойчивости в 1-ом приближении: 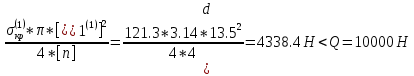 Условие устойчивости винта не выполнено, увеличиваем диаметр винта. 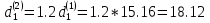 мм мм Так как  , то , то 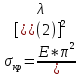 =218.9 МПа =218.9 МПаПроверка условия устойчивости в 1-ом приближении:  Условие устойчивости винта выполнено с большим запасом, принимаем в проект 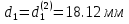 1.3 Выбор стандартных параметров резьбы Резьба трапецеидальная однозаходная ГОСТ 9484-81
1.4 Проверка выполнения условия самоторможения в резьбе Условие самоторможения имеет вид β ≤ ρ', где β – угол подъема винтовой линии резьбы, ρ'- приведенный угол трения в резьбе. Развернем на плоскость винтовую линию по среднему диаметру 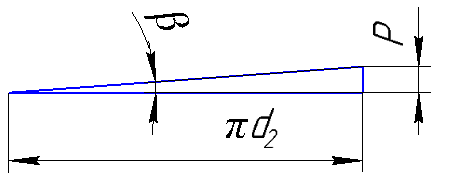 Рисунок 2 – Развертка винтовой линии по среднему диаметру  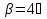 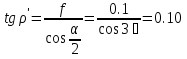   β =˂ ρ' Условие самоторможения выполнено. 1.5 Определение момента сил трения в резьбе  1.6 Момент сил трения на пяте винта  Рисунок 3 – Пята винта 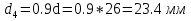 Так же должно быть выполнено условие 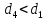 , следовательно, принимаем , следовательно, принимаем 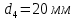 . .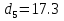 мм мм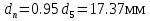 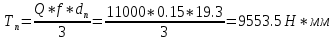 1.7 Проверка условия прочности на смятие в пяте винта Условие прочности на смятие : 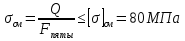  Условие прочности на смятие выполнено. 1.8 Определение длины рукоятки из условия равновесия моментов на винте Условие равновесия имеет вид ΣM0 = 0 – сумма моментов относительно оси винта Траб - Трез - Тп = 0 Траб = Трез + Тп , но известно, что: Траб = Ррабlр , тогда получаем  , где Pраб=100Н. , где Pраб=100Н.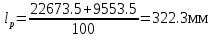 Принимаем длину рукоятки 300 мм. 1.9 Определение диаметра рукоятки В расчетной схеме рассматриваем рукоятку в виде консольной балки, жестко заделанной в головку винта. 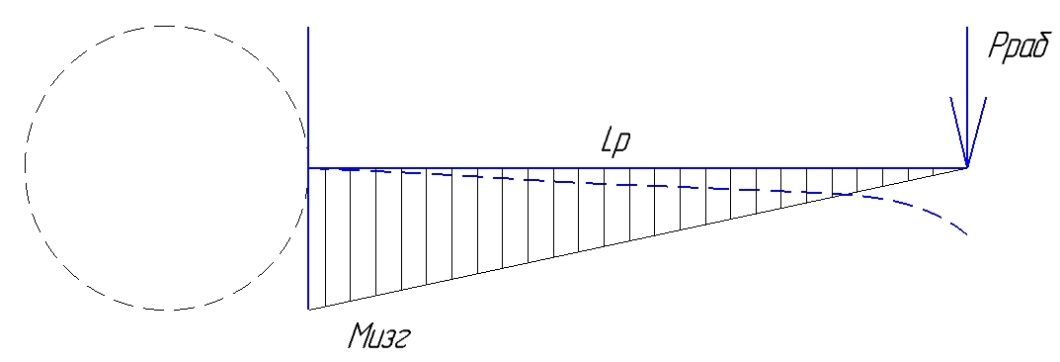 Рисунок 4 – Схема рукоятки Рукоятка работает на изгиб. Условие прочности на изгиб имеет вид  Отсюда требуемый диаметр рукоятки dр равен: 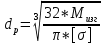  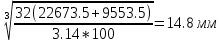 Принимаем диаметр рукоятки 15 мм 1.10 Проверочный расчет винта Винт в поперечном сечении работает на сжатие от силы Q и кручение от момента сил трения, либо в резьбе, либо в пяте в зависимости от места расположения опасного сечения винта по его высоте. 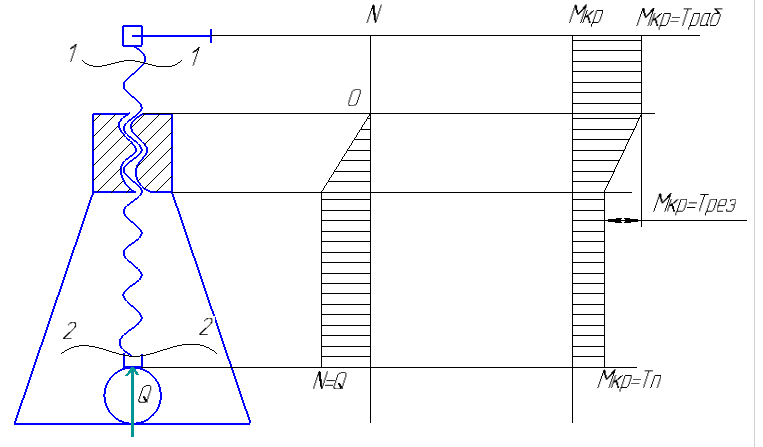 Рисунок 5 – Эпюры сил действующих на винт в поперечном сечении Условие прочности для опасного сечения 1-1 имеет вид:  МПа МПаУсловие прочности по эквивалентным напряжениям для сечения 2-2 имеет вид:  , где , где 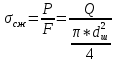 , ,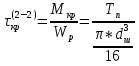  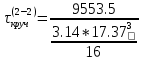 = 9.28 МПа = 9.28 МПа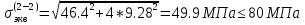 Условия прочности в сечениях 1-1 и 2-2 выполнены. Винт работоспособен. 2. Расчет гайки 2.1 Определение высоты гайки 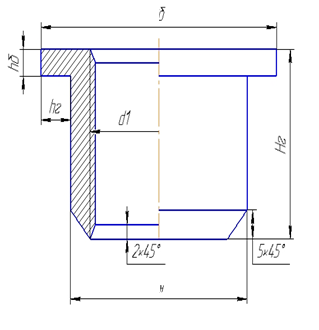 Рисунок 6 – Схема гайки Известно, что  = 2, тогда высота гайки = 2, тогда высота гайки 2.2 Проверка выполнения условия по числу витков в гайке Условие имеет вид: 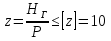   2.3 Определение наружного диаметра гайки Гайка в поперечном сечении работает на растяжение от силы Q и кручение от момента сил трения в резьбе. Условие прочности по эквивалентным напряжениям имеет вид:  Отсюда требуемый наружный диаметр гайки:  Проверяем толщину стенки 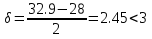 Принимаем δ=3 Тогда: 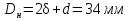 2.4 Определение диаметра бурта Опорная кольцевая поверхность бурта работает на смятие под действием силы Q. Условие прочности имеет вид : 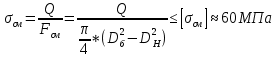 , отсюда , отсюда 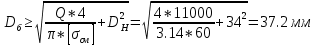 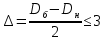 Принимаем ∆ =3, тогда Dб = DH+ 2∆ = 34 + 6 = 40 мм. 2.5 Определение высоты бурта Бурт по высоте под действием силы Q работает на срез. Условие прочности на срез имеет вид: 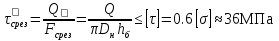  Вследствие погрешности изготовления гайки и корпуса возможно внецентренное нагружение бурта. В этом случае бурт работает на изгиб. Условие прочности на изгиб имеет вид: 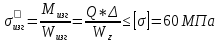 Момент сопротивления определим из расчетной схемы. Развернем кольцо бурта прямоугольного сечения на плоскость. Получим параллелепипед: 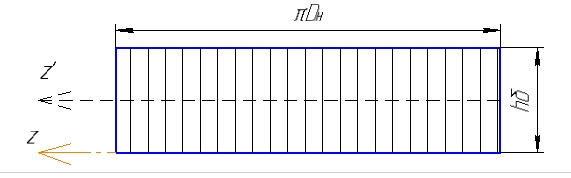 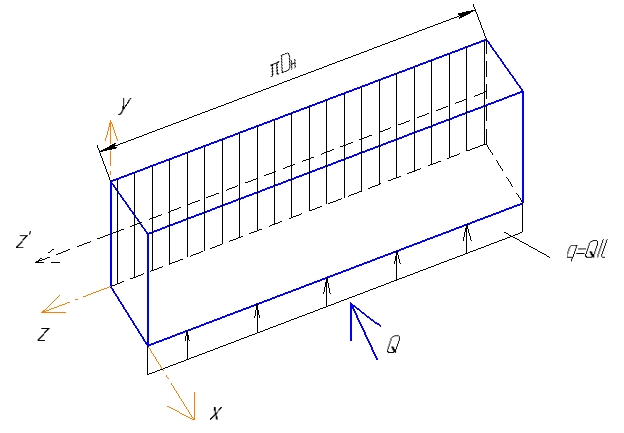 Рисунок 7 – Развертка кольца бурта 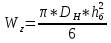 Тогда условие прочности имеет вид :  , отсюда требуемая высота бурта по изгибу: , отсюда требуемая высота бурта по изгибу: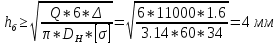 Принимаем в проект высоту бурта  3. КПД механизма 3.1 КПД резьбы  3.2 КПД зажима 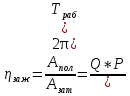 4. Расчет корпуса механизма Расчет стойки в виде тавра. 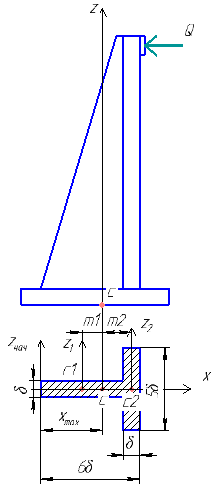 Рисунок 8 – Тавровая стойка Стойка работает на изгиб под действием силы Q. Условие прочности на изгиб имеет вид: 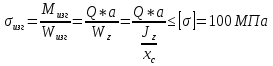 Определяем положение центра тяжести Т-образного сечения стойки: 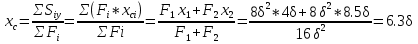 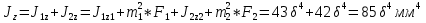 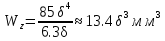 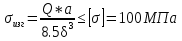 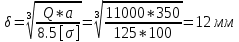 Принимаем  5. Расчет сварных швов 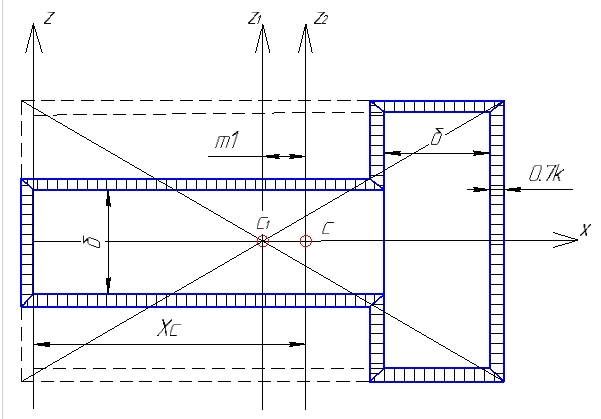 Рисунок 9 – Тавровая стойка Стойка приваривается к основанию. Вид соединения – тавровое. Соединение выполняется угловым швом. Расчет таких швов выполняется по касательным напряжениям среза к минимальным сечениям шва. 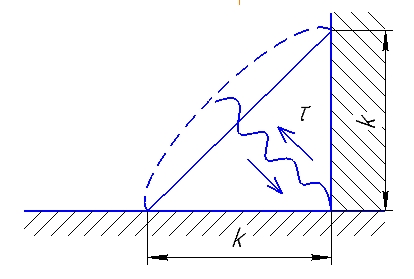 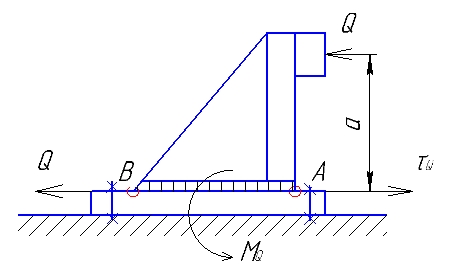 Рисунок 10 – Сечение шва тавровой стойки Шов воспринимает силу Q и момент MQ. Под действием Q в шве возникают касательные напряжения среза. 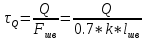 Длину шва найдем по упрощенной формуле. Упростим в расчетах контур сварного шва без потери надежности расчета. 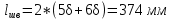 Принимаем в первом приближении катет шва k=6мм 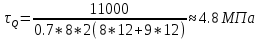 Под действием момента возникает напряжение τм:  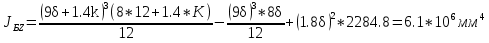 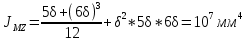 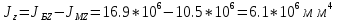 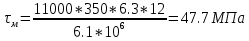 Условие прочности в опасных точках А имеет вид:  Шов неработоспособен. 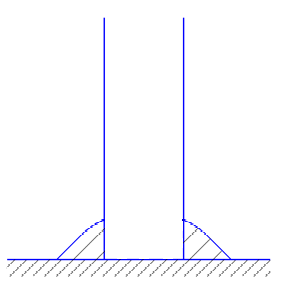 Рисунок 11 – Стыковой шов Тавровое соединение выполним стыковым швом. Расчет ведется по σм. Условие прочности имеет вид:  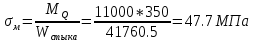 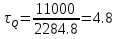 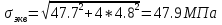 Условие прочности выполнено, шов работоспособен. 6. Расчет болтовых соединений 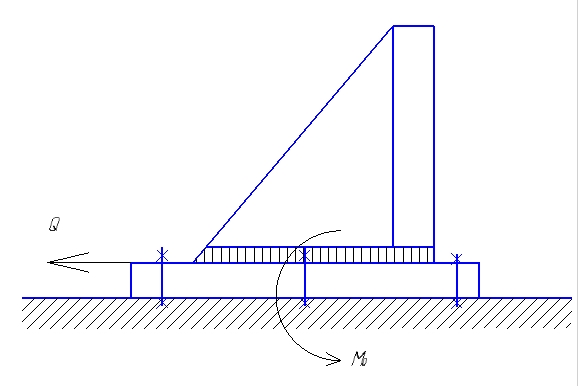 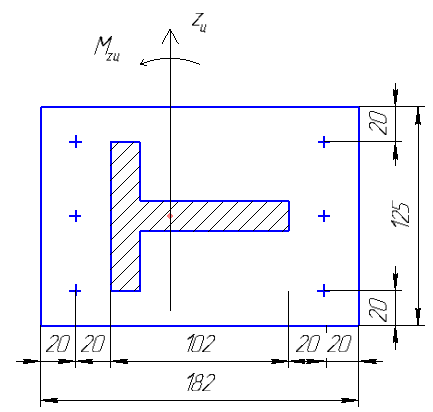 Рисунок 12 – Тавровая стойка в двух проекциях Расчет болтов необходимо проводить по условию не раскрытия стыка деталей. Условие не раскрытия стыка имеет вид: 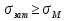 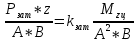  Определим дополнительную растягивающую силу RM на болтах, созданную моментом Mz. 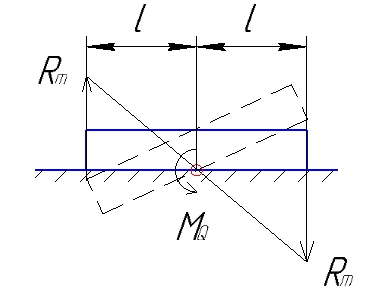 Рисунок 13 – Действие момента от силы Q  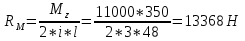 Полная растягивающая сила на болте равна: 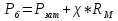 Для стальных деталей и сальных болта и гайки коэффициент внешней нагрузки  равен 0.2 … 0.3. равен 0.2 … 0.3.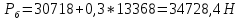 Болт работает на растяжение от силы Pб и кручение. Условие прочности по эквивалентным напряжениям имеет вид:  , отсюда диаметр болта равен: , отсюда диаметр болта равен: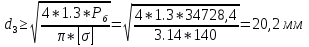 . .Увеличим класс прочности болтов для уменьшения диаметра примем 5.8 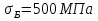 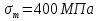 Допускаемое напряжение 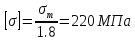 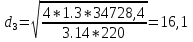 ГОСТ 9150-59 Резьба метрическая
Принимаем болт М20x90 Список литературы И.С.Кривенко "Сварные и болтовые соединения. Винтовые механизмы" ЛКИ 1983г.; Артемьев, Кривенко "Сварные и болтовые соединения. Винтовые механизмы" ЛКИ 1982г.; И.С.Кривенко "Проектирование винтовых механизмов" СПбГМТУ 2001г.; Артемьев, Кривенко "Проектирование винтовых механизмов" ЛКИ 1986г.; Иванова "Детали машин и основы конструирования" СПбГМТУ 2013г. |
