Пояснительная записка к курсовой работе по курсу Вычислительная техника и алгоритмические языки
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
6.3 Файл Data.cpp#include "Header.h" // Ввод данных с клавиатуры Data enterData(struct Data data) { do { system("cls"); cout << "Введите кол-во данных: "; cin.clear(); cin.sync(); cin >> data.N; if(data.N==0 | data.N <1||cin.fail()) { system("cls"); cout << "\a\n\n\n\t\t\t\tОШИБКА!" << endl; Sleep(1500); } } while (data.N == 0 | data.N < 1 || cin.fail()); data.U = new float[data.N]; data.p = new float[data.N]; system("cls"); cout << "Ввод зависимостей:" << endl; for (int i = 0; i < data.N; i++) { cout << "Зависимость " << i + 1 << ":" << endl; cout << "\tU[" << i + 1 << "]="; cin.clear(); cin.sync(); cin >> data.U[i]; if(cin.fail()) { cout << "\nВведенный тип данных не соответсвует типу переменной....Повторите ввод \a"; Sleep(800); system("cls"); cout << "Ввод зависимостей:" << endl; for (int j = 0; j < i;j++) { cout << "Зависимость " << j + 1 << ":" << endl; cout << "\tU[" << j + 1 << "]=" << data.U[j] << endl; cout << "\tp[" << j + 1 << "]=" << data.p[j] << endl; } i--; continue; } cout << "\tp[" << i + 1 << "]="; cin.clear(); cin.sync(); cin >> data.p[i]; if (cin.fail()) { cout << "Введенный тип данных не соответсвует типу переменной....Повторите ввод \a"; Sleep(800); system("cls"); cout << "Ввод зависимостей:" << endl; for (int j = 0; j < i; j++) { cout << "Зависимость " << j + 1 << ":" << endl; cout << "\tU[" << j + 1 << "]=" << data.U[j] << endl; cout << "\tp[" << j + 1 << "]=" << data.p[j] << endl; } i--; continue; } cout << endl; } return data; } // Ввод данных с файла Data readFile(struct Data data) { char FileName[100]; char txt[] = ".txt"; float buffer; system("cls"); cout << "Введите имя файла:" << endl; cin >> FileName; strcat(FileName, txt); ifstream in(FileName); if (in.fail()) { cerr << "Файл не открыт......\a" << endl; _getch(); } else { system("cls"); cout << "Файл успешно считан......" << endl; Sleep(500); in >> data.N; data.U = new float[data.N]; data.p = new float[data.N]; for (int i = 0; i < data.N; i++) { in >> data.U[i]; } for (int i = 0; i < data.N; i++) { in >> data.p[i]; } } in.close(); return data; } 6.4 Файл Menu.cpp#include "Header.h" void mainMenu() { system("cls"); // Очистка экрана cout << "\t\tВыберите действие:\n" << endl; cout << "\t1. Ввод данных с клавиатуры." << endl; cout << "\t2. Ввод данных с файла." << endl; cout << "\t3. Линейная зависимость." << endl; cout << "\t4. Логарифмическая функция." << endl; cout << "\t5. Квадратичная функция." << endl; cout << "\n" << endl; cout << "\t0. Выход." << endl; } 6.5 Файл Dependence.cpp#include "Header.h" float sumU(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += data.U[i]; } return S; } float sumP(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += data.p[i]; } return S; } float sumU_P(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += data.U[i] * data.p[i]; } return S; } float sumP_U_2(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += pow(data.U[i],2) * data.p[i]; } return S; } float sumU_2(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += pow(data.U[i], 2); } return S; } float sumU_3(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += pow(data.U[i], 3); } return S; } float sumU_4(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += pow(data.U[i], 4); } return S; } float sumP_2(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += pow(data.p[i], 2); } return S; } float sumU_P_minus(struct Data data) { float S = 0; for (int i = 0; i < data.N; i++) { S += data.U[i] - data.p[i]; } return S; } // Линейная зависимость вида y=aU+b void linearDependence(struct Data data, float* a, float* b) { *a = (data.N * sumU_P(data) - sumP(data) * sumU(data)) / (data.N * sumU_2(data) - pow(sumU(data), 2)); *b = sumP(data) / data.N - (*a) * (sumU(data) / data.N); } // Коэффициент корреляции float coefCorrelation(struct Data data, float a, float b) { // Числитель float top = sumU_P(data) / data.N - sumU(data) / data.N * sumP(data) / data.N; // Знаменатель float bot = sqrt((sumU_2(data) / data.N - pow(sumU(data) / data.N, 2))) * sqrt(sumP_2(data) / data.N - pow(sumP(data) / data.N, 2)); return top / bot; } float indexCorrelation(struct Data data, float Y[]) { float top = 0; float bot = 0; float avg = sumP(data) / data.N; for (int i = 0; i < data.N; i++) { top += pow(data.p[i] - Y[i], 2); bot += pow(data.p[i] - avg, 2); } return sqrt(1 - (top / bot)); } float determinant(float A[3][3]) { double **mas; float M; mas = new double*[3]; for (int i = 0; i < 3; i++) mas[i] = new double[3]; for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) mas[i][j] = A[i][j]; } for (int i = 1; i < 3; i++) { for (int j = i; j < 3; j++) { M = mas[j][i - 1] / mas[i - 1][i - 1]; // Находим главный элемент (на главной оси) for (int k = 0; k < 3; k++) { mas[j][k] = mas[j][k] - M*mas[i - 1][k]; // Обнуляем элементы } } } M = 1; for (int i = 0; i < 3; i++) { M *= mas[i][i]; // Находим определитель } for (int i = 0; i < 3; i++) delete[] mas[i]; delete[] mas; return M; } // Зависимость вида y=a0+a1U+a2U^2 void quadratic(struct Data data, float* a, float* b, float* c) { float A[3][3] = { {data.N, sumU(data), sumU_2(data)}, {sumU(data),sumU_2(data),sumU_3(data)}, {sumU_2(data), sumU_3(data), sumU_4(data)} }; float tempA[3][3]; float B[3] = {sumP(data),sumU_P(data),sumP_U_2(data)}; float main_det; // Главный определитель float det[3]; // Определители main_det = determinant(A); for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { tempA[i][j] = A[i][j]; } } for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) // заменяем i-ый столбец на столбец свободных членов { tempA[j][i] = B[j]; } det[i] = determinant(tempA); for (int j = 0; j < 3; j++) // возвращаем обратно значения { tempA[j][i] = A[j][i]; } } *a = det[0] / main_det; *b = det[1] / main_det; *c = det[2] / main_det; } // Ср. кв. отклонение float S(struct Data data, float Y[]) { float S = 0; for (int i = 0; i < data.N; i++) { S += pow(data.p[i] - Y[i], 2); } return S; } // Относительная ошибка float A(struct Data data, float Y[]) { float A = 0; for (int i = 0; i < data.N; i++) { A += fabs((data.p[i] - Y[i]) / data.p[i]); } return A / data.N; } 7 РАСЧЕТ В ЭЛЕКТРОННЫХ ТАБЛИЦАХНа рисунке 7.1 представлены расчёты для линейной зависимости. 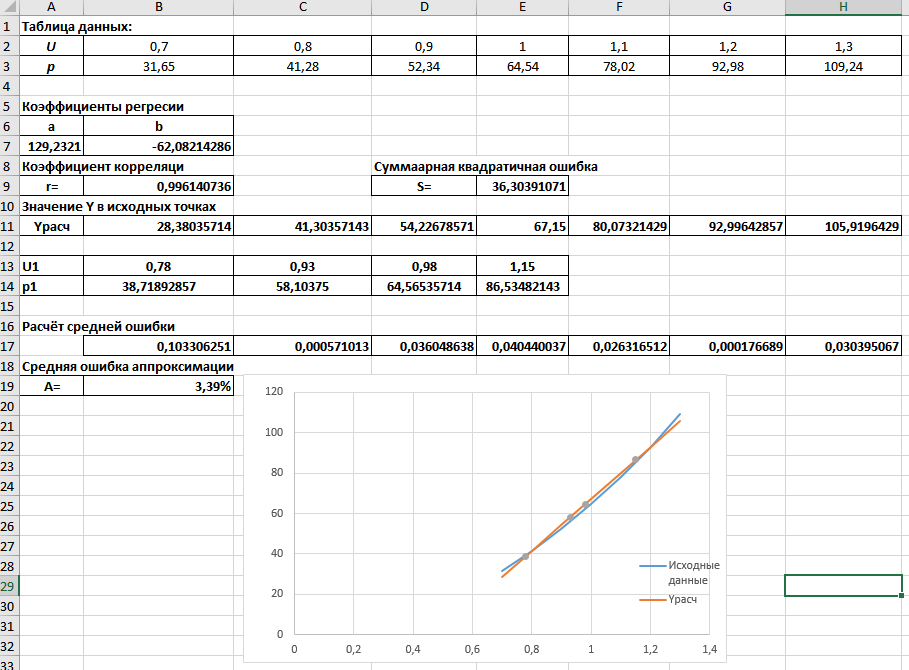 Рисунок 7.1 – Расчёты для линейной зависимости На рисунке 7.2 представлены расчёт для зависимости 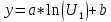 . .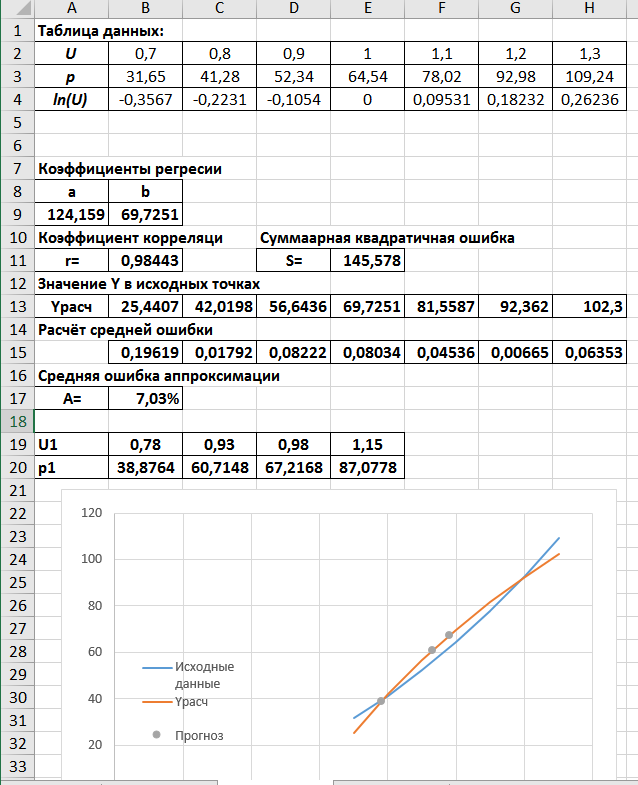 Рисунок 7.2 – Расчёты для зависимости 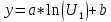 На рисунке 7.3 представлены расчёты для зависимости 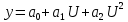 . . Рисунок 7.3 - Расчёты для зависимости 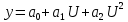 8 АНАЛИЗ РЕЗУЛЬТАТОВС помощью электронных таблиц MS Excel были проведены расчёты, и они полностью совпали с результатом работы программы. Это говорит о том, разработанный программный продукт полностью соответствует заданию и может применяться не только в учебных целях, но и практических. Были получены такие результаты: Для линейной зависимости: Коэффициент a = 129.2321; Коэффициент b = -62.0821; Коэффициент корреляции r = 0.9961; Суммарная квадратичная ошибка S = 36.3039; Значение p при 0.78U = 38.8789; Значение p при 0.93U = 58.10375; Значение p при 0.98U = 64.5653; Значение p при 1.15U = 86.5348; Средняя ошибка аппроксимации A = 3.39%; Для зависимости 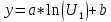 : :Коэффициент a = 124.159; Коэффициент b = 69.7251; Коэффициент корреляции r = 0.98443; Суммарная квадратичная ошибка S = 145.578; Значение p при 0.78U = 38.8764; Значение p при 0.93U = 60.7148; Значение p при 0.98U = 67.2168; Значение p при 1.15U = 87.0778; Средняя ошибка аппроксимации A = 7.03%. Для зависимости 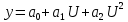 : :Коэффициент a0 = 1.015; Коэффициент a1 = -2.22024; Коэффициент a2 = 65.72619; Коэффициент корреляции r = 1; Суммарная квадратичная ошибка S = 0.01678; Значение p при 0.78U = 39.271; Значение p при 0.93U = 55.7968; Значение p при 0.98U = 61.9626; Значение p при 1.15U = 85.3846; Средняя ошибка аппроксимации A = 0.06%. Так же был проведён подбор различных зависимостей с помощью добавления линии тренда (Рисунок 8.1). Как видно по графику, коэффициент корреляции R=1 имеют зависимости: степенная и полином 2 степени.  Рисунок 8.1 – Подбор различных зависимостей ЗАКЛЮЧЕНИЕВ ходе выполнения курсовой работы были закреплены теоретические знания и практические навыки, полученные при учении курса «Информатика» и применение их при решении реальной задачи, изучение возможностей электронных таблиц при решении задач обработки экспериментальных данных. Разработанная программный продукт выполняет корреляционный и регрессионный анализ результатов выборочных замеров, получены результаты, на основе который можно сделать вывод о том, что между данными есть или нет заданных аналитических зависимостей. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫГурман В. Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Множественная регрессия = Applied Regression Analysis. — 3-е изд. — М.: «Диалектика», 2007. — С. 912. — ISBN 0-471-17082-8. Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа = Methoden der Korrelation - und Regressiolynsanalyse. — М.: Финансы и статистика, 1981. — 302 с. ПРИЛОЖЕНИЕ А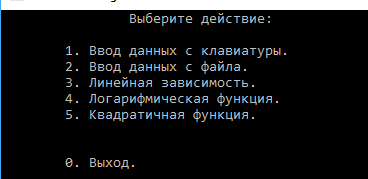 Рисунок А.1 – Главное меню программы 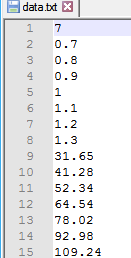 Рисунок А.2 – Содержание входящего файла 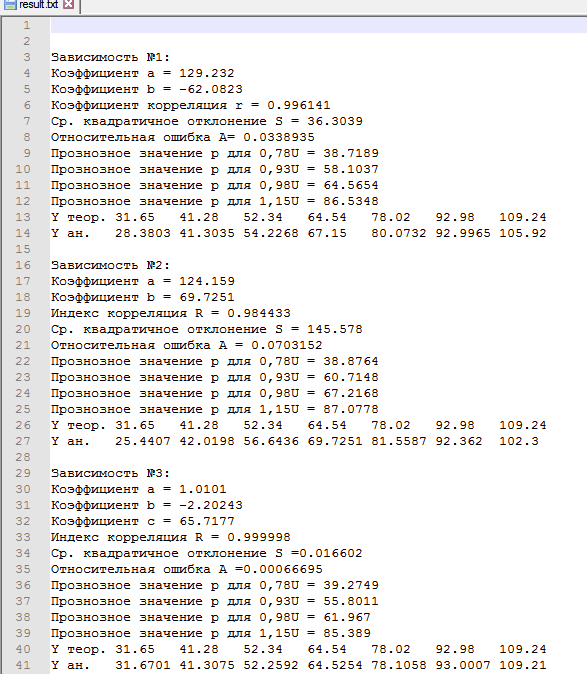 Рисунок А.3 – Результирующий файл  , , 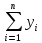 и т.д. из формулы (3.9); и т.д. из формулы (3.9);  , , 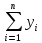 и т.д. и т.д.из формулы (3.9); |
