Курсач2. Пояснительная записка к курсовому проекту по дисциплине Теория экономических информационных систем
 Скачать 0.57 Mb.
|
|
Задание 6: Построить упорядоченное бинарное дерево с определенными значениями ключевых признаков и подравнять его. Сформируем бинарное дерево по вышеизложенному алгоритму, используя следующие значения ключевых признаков: 56, 46, 39, 76, 49, 97, 75, 39, 8, 59, 36, 80, 15, 46, 61 (рисунок 3.4). 56 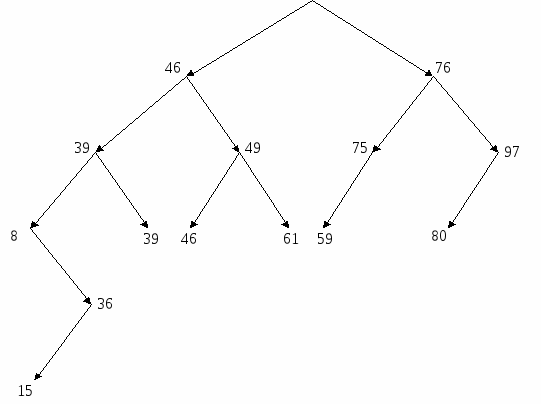 Рис. 3.4 – Формирование древовидной организации данных Ранг упорядоченного бинарного дерева можно сократить с помощью специальных преобразований – подравниваний. Преобразованное дерево называется подравненным. Назовем длиной ветви дерева разность между максимальным уровнем вершин этой ветви и уровнем вершины, определяющей ветвь. Бинарное дерево называется подравненным, если у каждой его вершины длина левой ветви отличается от длины правой не более, чем на единицу. Такие деревья называются подравненными по длине. Преобразование произвольного бинарного дерева в подравненное основано на понятии соседней записи. Соседняя слева запись – это запись с ключом, который непосредственно меньше ключа данной записи, а ключ соседней справа записи равен или непосредственно больше, чем ключ данной записи. Чтобы перейти от произвольного дерева к подравненному, надо для каждой несбалансированной записи (у которой разница длин ветвей больше единицы) выполнить ряд преобразований. После таких преобразований разнится длин должна сократиться. Наиболее сложно подравнивать полные записи. Для этого сначала выбирается соседняя запись с большей длиной ветви. Эта соседняя запись, со всеми выходящими из нее записями помещается на место подравниваемой. Далее вторая соседняя запись вместе с исходящими из нее записями исключается из дерева и заново перераспределяется в дерево по алгоритму включения новой записи. В последнюю очередь перераспределяется подравниваемая запись. Описанные действия производятся со всеми записями, нарушающими подравненность. Подравняем наше дерево, изображенное на рисунке 3.4:
Рис. 3.5 – Первая итерация подравнивания дерева
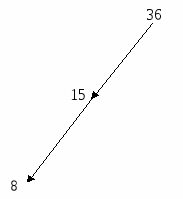 Рис 3.6 – Вторая итерация подравнивания дерева 3) подравниваем вершину 36 (разность 2). Вместо нее подставляем вершину 15; 15  Рис. 3.7 – Третья итерация подравнивания дерева 4) подравниваем вершину 39 (разность 3). Вместо нее подставляем вершину 49; 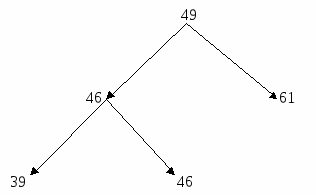 Рис. 3.8 – Четвертая итерация подравнивания дерева В результате мы получили подравненное дерево в котором нет ветвей с разностью длин больше 1 (рисунок 3.9). Задание 7: Поставить в вершинах бинарного дерева ключевые признаки от 1 до 12 так, чтобы дерево стало упорядоченным (подравнивать не надо). Исходное дерево изображено на рисунке 3.10. Как видим здесь имеется ошибка, т. к. получается, что элемент n одновременно больше и меньше элемента f. Если в правой ветви вместо него подставить другой элемент, например d, то решением головоломки может быть дерево, изображенное на рисунке 3.11. Р 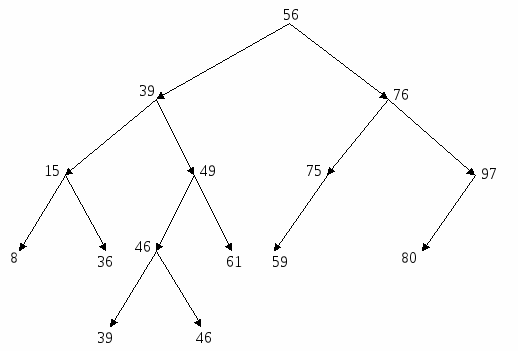 ис. 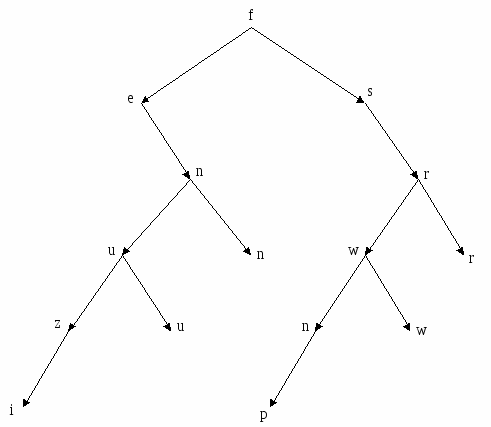3.9 – Подравненное бинарное дерево Рис. 3.10 – Головоломка 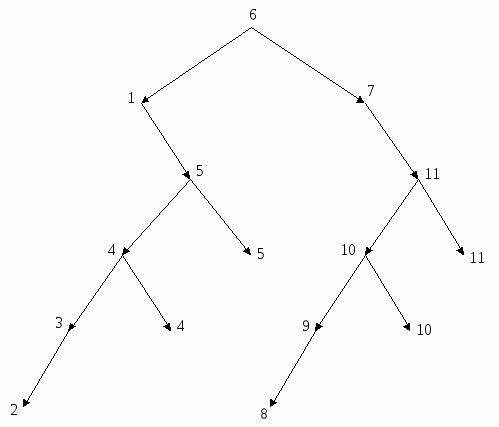 Рис. 3.11 – Решение головоломки с учетом замены элемента n в правой ветви на элемент d 3.2.2 Нелинейная списковая организация данных Нелинейный список – множество элементов, каждый из которых может быть либо записью, либо списком. Структура списка выражается формулой, в которой записи помечаются буквами, а списки заключаются в круглые скобки. Список, включенный в другой список, называется подсписком. Введенный аппарат списков намного шире, чем требуемый для представления деревьев. Он используется самостоятельно также в задачах искусственного интеллекта и анализа текстовой информации. Записи, входящие в список, могут занимать произвольный участок в памяти компьютера. Адреса связи, принадлежащие каждой записи, образуют звено связи. В звене однонаправленного списка два адреса: первыйуказывает на следующий элемент списка, второй – на подсписок или запись. Списковые структуры данных могут иметь два вида представления: с помощью аналитической записи и графической интерпретация структуры списка. Аналитическая запись списковой структуры строится по следующим правилам:
При определении структуры списка внешние скобки всегда отбрасываются, а далее каждой открытой скобке находится соответствующая ей закрытая скобка. Элементы, заключенные в скобки являются подсписками и объявляются сложными элементами. Элементы, обозначенные буквами называются простыми. Задание 8: Дать графическую интерпретацию списка, заданного аналитическим выражением: (((b, a), (b, ((a, (b)), (a, (b))), (b, a))), b). Разобьем список на сложные и простые элементы:
Г 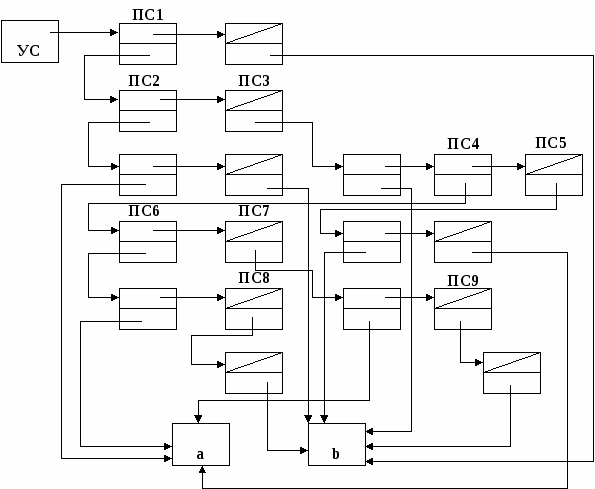 рафическая структура списка представлена на рисунке 3.12.Рис. 3.12 – Нелинейный список в памяти компьютера Для задания однонаправленной списковой структуры необходима следующая ассоциативная информация:
Последовательная, списковая и бинарная организация данных предназначены для решения общей задачи – обработке записей с одним ключевым атрибутом.
Возможность определения места хранения данных используется также при размещении данных согласно адресной функции. Упорядоченность записей по значениям ключа в этом случае, вообще говоря, не соблюдается. Адресной функцией называется зависимость i = f(A), где i – номер(адрес) записи, А – значение ключевого атрибута. Адресная функция может вырабатывать одинаковые значения i для значений ключей, принадлежащих разным записям, которые в данном случае называются синонимами. К адресной функции предъявляются следующие требования:
Простейшая адресная функция имеет вид i = A – c, где с – константа. Необходимо определить минимальное значение ключевого атрибута Аmin и максимальное значение Аmax. Тогда с = Аmin – 1. Необходимый участок памяти данных должен иметь размер [Amax – Amin + 1] запись. Записи-синонимы связываются в цепочки с помощью адресов связи, они занимают дополнительную (резервную) память. Недостатком данной адресной функции является большой объем используемой памяти, если Amax – Amin много больше, чем количество записей М исходного массива. Задание 9: Построить адресную функцию вида i = A – c. Значения ключей следующие: 65, 72, 73, 66, 69, 76, 74, 81, 78, 77, 63, 74, 69, 73, 64, 77, 75. Аmin = 63, Amax = 81, c = Amin –1 = 63 –1 = 62, n = [Amax – Amin +1] = 81 – 63 + 1 = 19.
Рис. 3.13 – Организация записей в соответствии с адресной функцией i = A – c Указанного выше недостатка (большой объем используемой памяти) лишена адресная функция вида i = ост (A/m), где m – целое число, ОСТ – остаток от деления А на m. Значение m принимается равным просому числу, которое непосредственно больше или меньше числа записей М: m = M ± 1. Выделяются две зоны памяти – основная и резервная. Основная зона содержит m записей. Резервная зона предназначена для размещения записей-синонимов. При формировании данных согласно адресной функции сначала производится заполнение основной зоны. Если при этом позиция основной зоны, получнная при вычисленияи, уже занята, то текущая запись помещается в резервную зону и адресуется из позиции основной зоны. В дальнейшем при такой ситуации наращивается цепочка в резервной зоне. Задание 10: Построить адресную функцию вида i = ост(А/m). Значения ключей следующие: 78, 49, 51, 81, 21, 26, 47, 75, 51, 42, 26, 84, 57, 40, 84, 65, 42. М = 17, m = M – 1 = 16. 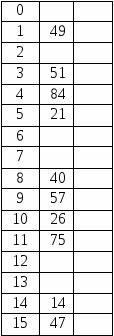  81     51 42  26   84 65 42 Рис. 3.14 – Организация записей в соответствии с адресной функцией А = ОСТ(А/m)
Индексом называется набор адресов и ключей записей, которые выбираются из основного массива по определенному закону. Отдельный элемент набора индексов также называется индексом. Существует три разновидности индексов:
Сплошной индекс связан с созданием инвертированного массива ключевых атрибутов к основному массиву. Элементы, составляющие инвертированный массив называются группами. Каждая группа содержит значение ключевого атрибута, имеющегося в массиве, и набор адресов записей, содержащих этот ключ. Индексно – последовательный массив (К – индекс) представляет собой последовательный массив, отсортированный по значениям ключевого атрибута, к которому создается дополнительный массив индексов. В индекс вносится информация о записях, номера которых образуют арифметическую прогрессию с шагом d > 1, причем первый индекс адресует первую запись. Основной массив, дополненный таким индексом называется индексно-последовательным. Индекс такого типа называют К - индексом (от слова "ключ"). Шаг арифметической прогрессии для К – индексов равен:  , где М – количество элементов в исходном массиве.Рандомизированный массив (А - индекс) получаем если ключ записей, информация о которых выносится в индекс, приближенно образуют арифметическую прогрессию. Первый индекс адресует первую запись. Индексы такого типа называют А - индексами (от слова "адрес"). Точное описание рандомизированного индекса состоит в следующем: А – индекс с номером i хранит адрес записи основного массива, ключ которой равен или непосредственно больше значения pi ≥ p1 + z(i – 1), где z - константа (шаг арифметической прогрессии), р1 – значение ключа первой записи основного массива. Точной формулы для шага арифметической прогрессии не существует, обычно рекомендуют: z ≤ 2 max (pi – pi-1). |
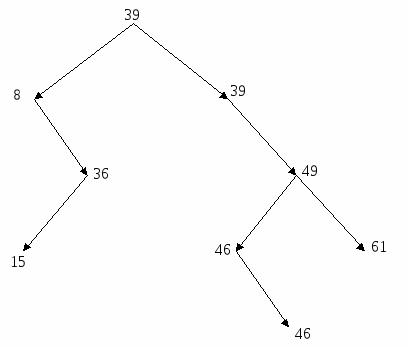оравниваем вершину 46 (разница длин исходящих ветвей 2). Вместо нее подставляем вершину 39;
