Оценка надежности функционирования районной энергосистемы в различных эксплуатационных режимах. Пояснительная записка по дисциплине Режимы и надежность энергосистем
 Скачать 1.21 Mb.
|
2. ОЦЕНКА РЕЖИМНОЙ (БАЛАНСОВОЙ) НАДЕЖНОСТИ РЭСВ задаче режимной надёжности рассмотрим энергосистему в целом, основными элементами системы представлены нагрузкой и генерацией. Решение данной задачи основано на исследовании потока случайных событий возникновения дефицита мощности в РЭС. Энергосистему при этом представляют упрощенно концентрированной и неоднородной системой. Первым шагом для оценки режимной надежности будет построение модели нагрузки энергосистемы. Вторым шагом будет формирование модели генерирующей части. Третий шаг – это формирования модели всей энергосистемы путем рассмотрения двух вышеописанных совместных событий и получения нового потока случайных событий. После построения модели необходимо определить коэффициент бездефицитной работы и коэффициент недоотпуска электроэнергии. При неудовлетворении данных показателей нормативным значениям, следует провести мероприятия по повышению балансовой надежности РЭС. 2.1. Формирование модели нагрузки Событийная модель нагрузки Н{НPHj}должна описать возможные ее состояния за год (рис. 3). Каждая j-я ступень нагрузки – это событие НРНj, состоящее в случайном формировании нагрузки определенной мощности РНj. Нагрузка принимает некоторое фиксированное значение. Тогда полная группа событий опишется: Н (НРН1, НРН2, …, НРН8760), где индексы РНj показывают условия возникновения элементарных событий. Событийная модель для графика на рис. 2 средствами алгебры запишется следующим образом: Н = НРН1+НРН2+…+НРН8760, где знак «+» - то же, что «или», обозначает операцию логического сложения [1]. Ряд распределения нагрузки в ЭЭС, ее продолжительность и результаты расчета вероятностей их возникновения за год приведены в таблице 5. Расчет вероятности возникновения нагрузки производился путем выделения соответствующего диапазона нагрузки от общей нагрузки энергосистемы за год. Модель мощности нагрузки энергосистемы представлена поток случайных величин мощностей энергосистемы в таблице 5. Таблица 5 – Поток случайных величин мощностей энергосистемы
2.2. Формирование модели генерирующей части Располагаемая мощность системы величина случайная, она зависит от состояния генераторов. Каждый из генераторов может находиться лишь в двух состояниях – работоспособном или вынужденном простое. Каждое состояние характеризуется своим коэффициентом – коэффициентом готовности Кг и коэффициентом вынужденного простоя Кп. Коэффициент готовности представляет собой отношение времени исправной работы к сумме времен исправной работы и вынужденных простоев объекта, взятых за один и тот же календарный срок. Коэффициент вынужденного простоя определяется отношением времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев объекта, взятых за один и тот же календарный срок. Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью: КП =1−КГ (1.5) Согласно исходным данным: коэффициент вынужденного простоя  и продолжительности планового простоя за год ремонтов  месяц для всех генерирующих агрегатов.Генерирующая часть модели представлена однотипными энергоблоками с единичной мощностью РГ. На правой оси графика отложены мощности, соответствующие состояниям генерирующей части РСi, случайным образом возникающие вследствие аварийных остановов одного и двух энергоблоков. События останова отдельных блоков  являются совместными – они могут возникать одновременно с другими аналогичными событиями. Случайные события отказов энергоблоков формируют случайные значения располагаемой мощности в энергосистеме С(СРС1, СРС2). Событийная модель для данного случая алгеброй логики записывается следующим образом: С = С3Pг+ С2Pг+ С1Pг+ С0Pг, где С3Рг, С2Рг, С1Рг и С0Рг – случайные события появления располагаемой мощности энергосистемы вследствие отказов энергоблоков. Согласно рекомендациям [1] при количестве генераторов 4 и менее, будет полезно рассмотреть вероятность возникновения события для лучшего усвоения методики, путем составления таблицы состояния работы генераторов и определения вероятности каждого события. Определим коэффициент вынужденного простоя и коэффициент готовности генераторов, которые будут соответствовать вероятности нерабочего и рабочего состояния отдельного генератора, соответственно. Коэффициент вынужденного простоя генераторов Фомской ТЭЦ определяется по выражению:  (1.8)где  – коэффициент вынужденного простоя генераторов Mгод – количество месяцев в году Коэффициент вынужденного простоя генераторов Фомской ТЭЦ равен:  Коэффициент готовности на основании формулы (1.5) равен: КГ = 1− КП = 1− 0,0458 = 0,9542, где  – коэффициент готовности генераторов.Модель генерирующей части энергосистемы представлена потоком случайных величин мощностей генерации в таблице 6 Таблица 6 – Поток случайных величин генерирующей части
Вероятность наступления состояния для двух генераторов одновременно определяется путем произведения состояний, т.е. произведением нескольких состояний называется состояние, состоящее в совместном появлении всех этих состояний. Так, например, возможно состояние, когда и Г1 и Г2 будут находиться в работе. Вероятность работы первого генератора KГ1=0,9542, вероятность работы второго генератора KГ2=0,9542, т.о. вероятность работы двух генераторов равна K1= KГ1 ∙KГ2=0,9105. Соответственно K2=0,0437, K3=0,0437 и K4=0,0021. 2.3. Формирование модели энергосистемы Модель энергосистемы является случайной величиной, зависит от того сколько подключено нагрузок, от того сколько генераторов находится в работоспособном состоянии. Т.е. является результатом наложения событий для поток случайных событий генерирующей и нагрузочной части. Совпадение процессов производства и потребления во времени выразим через произведение вероятностных моделей этих процессов:  , (1.9)где  ,  и  – ряды распределений соответственно энергосистемы, генерирующей части и нагрузки. Для практических нужд модель делиться на две части: первая будет характеризовать нормальное бездефицитное состояние (наклонный шрифт), а вторая – дефицитные состояния (жирный шрифт) (табл. 7). Такое представление модели приблизит ее к практически важной задачи оценки недоотпуска электроэнергии следствие возникновения дефицитных состояний. Анализ модели будет состоять в выявлении бездефицитных состояний энергосистемы (профицита) с избытком генерирующих мощностей и дефицитных - с недостатком генерирующих мощностей. Дефицитные состояния являются нежелательными для энергосистемы и в норме они должны составлять малую долю от нормальных бездефицитных состояний. Совместное рассмотрение потока событий появления мощности нагрузки Н и потока отказов энергоблоков Г, формирующих располагаемую мощность системы С позволяет увидеть полную группу состояний энергосистемы: Э=Н×С, (1.7) где Э, Н и С – логические событийные модели соответственно энергосистемы, нагрузки и генерирующей части системы. Модель энергосистемы представлена потоком случайных величин возникновения дефицита и избытка мощности в энергосистеме в таблице 7. Таблица 7 – Поток случайных величин возникновения дефицита и избытка мощности в энергосистеме
2.5. Определение показателей надежности Расчет коэффициента бездефицитного состояния энергосистемы Коэффициент бездефицитной работы по формуле (1.1), в несколько измененном виде записывается следующим образом: 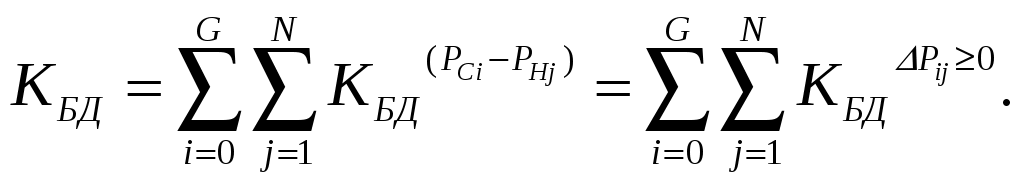 (1.6)Здесь под «коэффициентом» понимается вероятность, запись  читается, как вероятность события ij, состоящего в том, что располагаемая генерирующая мощность энергосистемы PСi превышает требующуюся для потребителя PHj. Верхний индекс ∆Pij = (PСi −PHj)≥0 показывает, вероятность лишь таких бездефицитных событий. Из всего множества бездефицитных событий, которые происходят в течение года, путем суммирования их вероятностей возникновения определяется одно число, показывающее вероятность бездефицитного состояния энергосистемы  .Сказанное выше иллюстрирует рисунок 5, связывающей потоки случайных событий появления мощностей нагрузки и генерации, где PН, PНj, PС, PСi –потребляемая мощность нагрузки, ее значения и располагаемая мощность системы и ее значение; PГ – единичная мощность энергоблока. Функциональное состояние энергоблоков обозначается буквами: «Г» – в работе, «О»− остановлен. Дефицитные состояния – те состояние при которых нагрузка энергосистемы больше, чем генерация. 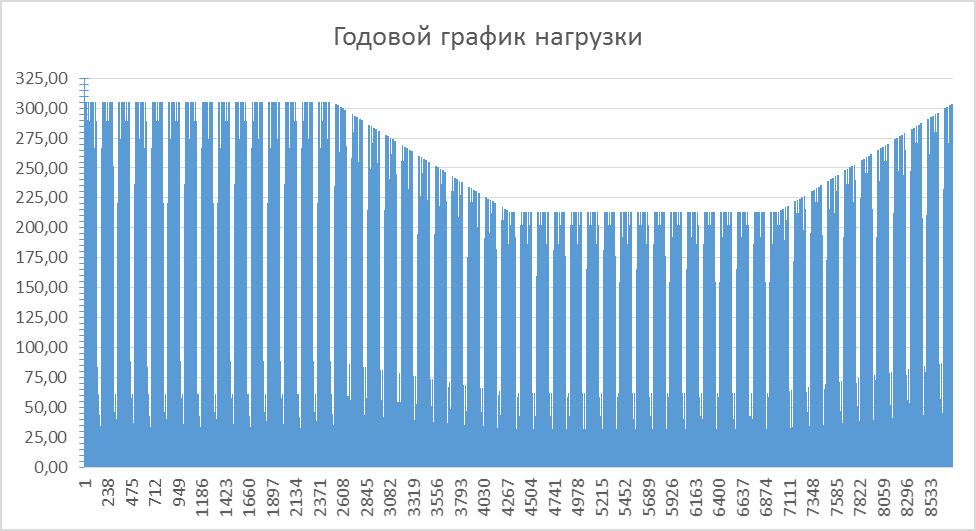  Г, Г Г, О О, Г О, О Рисунок 4 – Годовая модель состояний ЭЭС Для всех состояний энергосистемы при отсутствии в ней дефицита мощности, коэффициент бездефицитной работы равен:  .Определение индекса надежности энергосистемы Индекс надежности энергосистемы определяется по формуле (1.2):  Для определения математического ожидания электроэнергии за год вследствие возникновений дефицитов мощности воспользуемся следующим выражением:  . (1.11)На основании таблицы 9 (красный шрифт) математическое ожидание электроэнергии за год вследствие возникновений дефицитов мощности равно:  МВт.Годовая потребность в электроэнергии определяется по графику годовой продолжительности нагрузки (прил. Б, рис. 1Б):  МВтКоэффициент готовности энергосистемы равен: 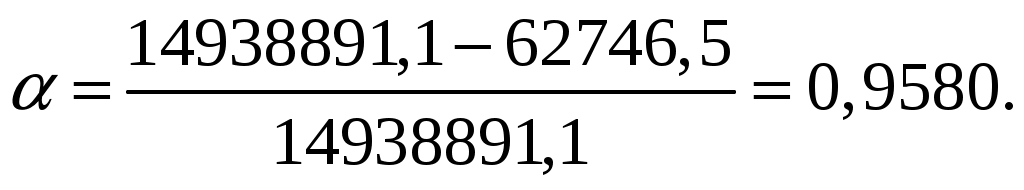 Сравнение нормативных коэффициентов с рассчитанными показывает, что коэффициент бездефицитной работы и коэффициент готовности энергосистемы меньше нормативного: КБД расч = 0,9517<0,996 = КБД норм; 𝛼расч = 0,9580< 0,999 = 𝛼норм. Необходим дополнительный резерв генерируемой мощности. 2.6. Определение показателей надежности с учетом ввода резерва В связи с несоответствием показателей надежности системы с нормативным, необходимо ввести резерв генерирующей мощности путем добавления дополнительных генераторов. После ввода резерва необходимо осуществить пересчет модели генерации, энергосистемы и показателей надежности с учетом введенного резерва по аналогии с пунктами с вышеприведенными пунктами. Добавим два генератор: первый номинальной мощностью 220 МВт (Г3), второй номинальной мощностью 110 МВт (Г4), тогда суммарная мощность генерирующего оборудования ТЭЦ равна: РгΣ = 2 · 220 + 2∙110 = 660 МВт. На основании внесенных изменения вновь составим таблицу состояний генераторов и определим вероятность возникновения состояния и генерируемую мощность. Таблица 7 − Возможные состояния генерирующих агрегатов и вероятность их возникновения при вводе резерва
Вероятность события по генерации определенной мощности определяется как произведение вероятностей отдельных событий, в которых генерируется её эта мощность. Так например вероятность того, что генерирующая часть будет генерировать 110 МВт, будет равна произведению вероятностей событий 7, 8, 9 и 10, т.о. К330= К7∙ К8∙ К9∙ К10=0,001909896∙0,001909896∙ ∙0,001909896∙0,001909896=0,005729689 Модель энергосистемы представлена потоком случайных величин возникновения дефицита и избытка мощности в энергосистеме в таблице 8. Таблица 8 – Поток случайных величин возникновения дефицита и избытка мощности в энергосистеме
Коэффициент бездефицитной работы при вводе резерва равен:  Коэффициент готовности энергосистемы при вводе резерва равен: 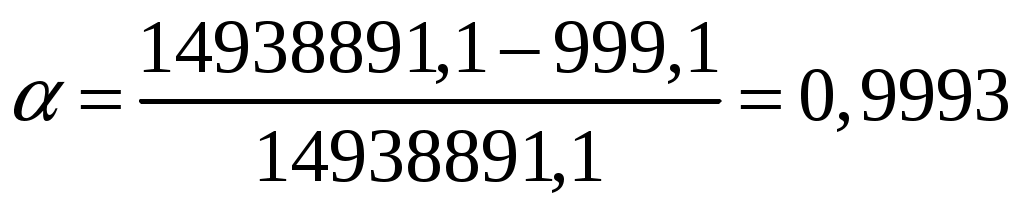 Сравнение нормативных коэффициентов с рассчитанными показывает, что коэффициент бездефицитной работы и коэффициент готовности энергосистемы больше нормативного: КБД расч = 0,9972 >0,996 = КБД норм; 𝛼расч = 0,9993> 0,999 = 𝛼норм. следовательно, вводимый резерв обеспечивает надежное и бесперебойное электроснабжение потребителей. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||