Лабораторная работа №7. Практическая работа Исследование эмпирической зависимости теплоемкости вещества от температуры. Понятие статистической зависимости
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
|
Практическая работа № 7. Исследование эмпирической зависимости теплоемкости вещества от температуры. Понятие статистической зависимости Две величины (например, х и у), могут быть независимыми, либо связанными функциональной, либо статистической зависимостью. Функциональная зависимость - каждому значению независимой переменной х соответствует строго одно значение у (отклик). Статистическая зависимость двух величин - изменение одной из величин влечет изменение распределения другой величины. Этапы построения статистических моделей: · Выбор вида модели (построение гипотезы о виде функции); · Численная оценка параметров модели; · Проверка адекватности полученной модели. Метод наименьших квадратов. Пусть требуется исследовать зависимость Y=f(X), заданной табличным способом в виде набора пар чисел (Xi,Yi), причем величины X и Y получены экспериментально, в одних и тех же экспериментах. Задача состоит в установлении функциональной зависимости Y=Ф(X) по результатам измерений (X,Yi), где i=1,2,...,n. Пусть аппроксимирующая функция Ф(X) может быть представлена в виде Ф(X,a1,а2,...,ак), где ai,a2,...,ai<- неизвестные параметры. Тогда результаты измерений можно представить как У1 = Ф(Х,а1,а2,...,ак)+Х1, где 30 - случайные величины, характеризующие погрешности эксперимента. Обычно предполагают, что они - независимые, нормально распределенные, с нулевым математическим ожиданием и одинаковыми дисперсиями. Задача состоит в том, чтобы по опытным данным наилучшим образом определить значения параметров aк. При этом в методе наименьших квадратов считается, что наилучшими будут те значения параметров aк, при которых сумма квадратов отклонений расчетных величин Yi от экспериментальных окажется наименьшей, т.е. S = Zi (Y - Ф(Х,а1,а2,...,ак))2 => min. Таким образом, аппроксимирующая функция (в отличие от задачи интерполяции) не обязательно проходит через экспериментальные точки (напомним, полученные с возможной погрешностью). Выбор вида модели Выдвигают гипотезу о виде функции Ф(X,а1,а2,...,ак). В общем случае это может быть функция нескольких переменных, и она не обязательно будет линейной (по параметрам). Для начала рассмотрим случай парной регрессии (один отклик Y и одна независимая переменная X). Полиномиальная регрессионная аппроксимирующая функция: Ф(Х)=ао+а1Х+а2Х2+ ....+ акХк является линейной относительно параметров aк, поскольку все множители при aк являются степенями экспериментальных значений X, т.е. являются числами. Например, линейная полиномиальная модель имеет вид Ф(X)= у, = a0+aiX, а квадратичная полиномиальная модель: Ф(X) = Ух=ao+aiX + а2 X2 Кроме полиномиальной модели есть еще ряд моделей, которые являются внутренне линейными по параметрам и могут быть сведены путем несложных алгебраических преобразований к полиномиальной модели. Численная оценка параметров модели По имеющимся экспериментальным данным определяют численные оценки параметров. Для отыскания минимума функции S нужно приравнять нулю ее частные производные по параметрам: ∂S/∂a0= О ∂S/∂ai= О ∂S/∂ak = О Если Ф(Xi,ai,a2,...,ak) линейна по параметрам, то полученная в результате дифференцирования система уравнений является системой линейных алгебраических уравнений. Решая ее аналитически или численными методами, можно получить значения параметров ai,a2,...,ak. Проверка адекватности модели После оценки коэффициентов уравнения необходимо проверить, насколько хорошо расчетная прямая (кривая) описывает данные (проверить адекватность уравнения). Для этого необходимо рассчитать следующие величины: Остаточная дисперсия: Smo =--------г------ Л^У - У п-к-1 =1 JlJ где yˆ i - расчетные по выбранному уравнению значения y. yi - экспериментальные значения y. n – число экспериментов (объем выборки) k – число параметров при переменных уравнения регрессии (без свободного члена). k=1 для линейной модели, k=2 для квадратичной модели и т.д. 1 JL Дисперсия относительно среднего значения:v П-1 i=1 где 1 « у = —2^i У; - среднее значение у в п экспериментах п г=1 Критерий Фишера равный отношению двух дисперсий: f v s2 ОСТ Вычисленное значение F сравнивают с Fтабл, полученным по статистическим таблицам для критерия Фишера. Справочные значения Fтабл зависят от трех параметров Fтабл(0.05, n-1,n-k-1) Если F>Fтабл, то считается что вид функции был выбран правильно, т.е. математическая модель описания эксперимента адекватна. Иногда для проверки адекватности модели используют коэффициент детерминированности R2, который изменяется в пределах от 0 до 1. Если он равен 1, то выбранная модель абсолютно адекватна экспериментальным данным; если он равен 0, то никакой связи между экспериментом и выбранной моделью нет. Обычно по степени близости R2 к 1 судят о мере адекватности математической модели. Задание Построить график температурной зависимости теплоемкости вещества в заданном температурном диапазоне по справочным данным, выбранным из базы данных в соответствии с номером варианта. Определить параметры линейной и квадратичной моделей зависимости теплоемкости вещества от температуры Cp=f(T), используя линию тренда. Рассчитать значения критерия Фишера и проверить адекватность полученных моделей. Определить параметры линейной и квадратичной моделей зависимости теплоемкости вещества от температуры Cp=f(T) и оценить адекватность полученных моделей, используя пакет анализа данных. Сделать вывод о применимости линейной и квадратичной моделей для решения данной задачи. Этапы выполнения работы 1. Открыть с сервера из папки с заданиями файл VARIANT.XLS с вариантами заданий. Перейти на рабочий лист ВАРИАНТЫ. С помощью Фильтра задать условия отбора записей по номеру работы и варианта и получить название вещества. Перейти на рабочий лист ТЕПЛОЕМКОСТЬ. С помощью Фильтра задать условие отбора записей по названию вещества и получить таблицу значений теплоемкости заданного соединения. 2. Создать в новом файле электронную таблицу для построения графика температурной зависимости теплоемкости и сохранить новый файл в своем рабочем каталоге. В первой строке таблицы расположить название работы. Во вторую строку ввести номер варианта. В третью строку ввести формулу соединения. В четвертую строку ввести заголовки столбцов T и Cp. Выделить название работы и названия столбцов жирным шрифтом  Скопировать с рабочего листа ТЕПЛОЕМКОСТЬ файла VARIANT.XLS справочные значения теплоемкости заданного вещества. Построить график температурной зависимости теплоемкости заданной соли. Ряд данных должен содержать только черные маркеры данных без соединительных линий. Диаграмма должна иметь название, легенду и названия осей. 
3. Построение эмпирической зависимости. Выделить диаграмму, используя кнопку «плюс» справа от диаграммы вставить линию тренда. Используя пункт Дополнительные параметры, на диаграмме уравнение и величину R2. Формат линии тренда Параметры линии тренда т <5» О ill  ры линии тренда Lif* С ' Экспоненциальная \jf 0*0 Линейная /^^ Логарифмическая \y\J- (.'Полиномиальная Степень \_±у- О Степенная I /^ ,- Скользящее ._. _ И_ ° средне ПгрИОД 2 Название линии тренда (•,' Автоматически Линейная [Ср ■. ■ Другое Прогноз Вперед на | 0,0 перис Назад на | 0,0 перис I I установить пересечение М показывать уравнение на диаграм1ме ^ поместить на диаграмму величину достоверности аппроксимации [RA2] На той же диаграмме вставить квадратичную (полиномиальную степени 2) модель, показать на диаграмме уравнение и величину R2. 4. Форматирование диаграммы. Расположить уравнения на диаграмме таким образом, чтобы они не перекрывали ряды данных. Линейное уравнение и линию тренда выделить синим цветом, квадратичное уравнение и линию тренда выделить красным цветом. Для форматирования уравнений выделить уравнение и использовать контекстное меню Формат подписи линии тренда. Установить экспоненциальный формат чисел с тремя десятичными знаками. 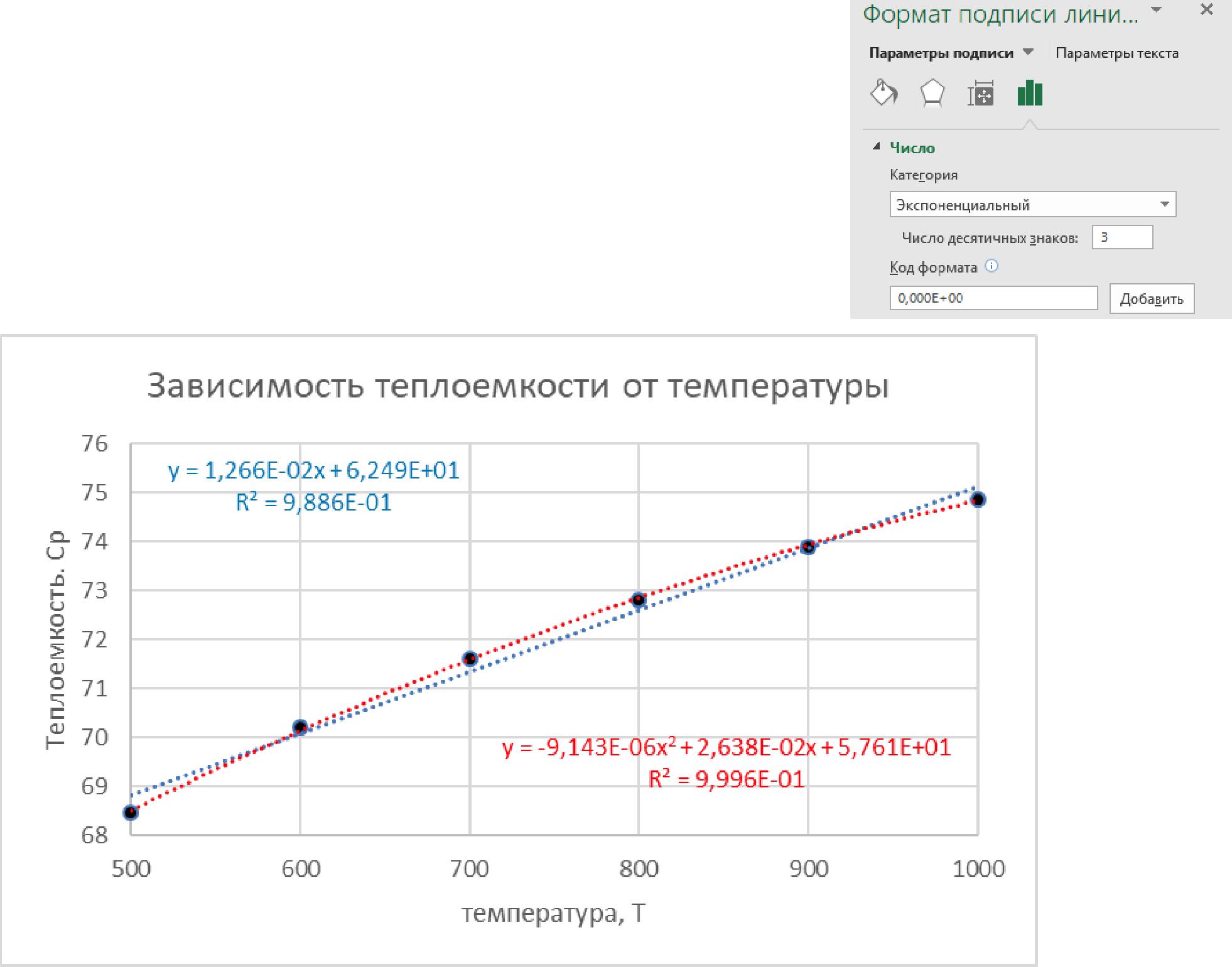 5. Проверка адекватности полученных моделей. Ввести заголовки столбцов жирным шрифтом, скопировать справочную таблицу данных и рассчитать количество экспериментальных точек n, среднее значение Ycp, квадраты отклонений экспериментальных значений от среднего и дисперсию относительно среднего значения. В следующих столбцах ввести заголовки «Линейная модель» и «Квадратичная модель». Над заголовками столбцов ввести названия коэффициентов моделей. Значения коэффициентов моделей взять из уравнений, полученных при помощи линий тренда. Рассчитать значения теплоемкости вещества, используя абсолютные ссылки на введенные коэффициенты. Расчетные значения должны иметь два десятичных знака. Рассчитать квадраты отклонений линейной и квадратичной модели от экспериментальных значений, остаточные дисперсии, табличные и экспериментальные значения критерия Фишера. 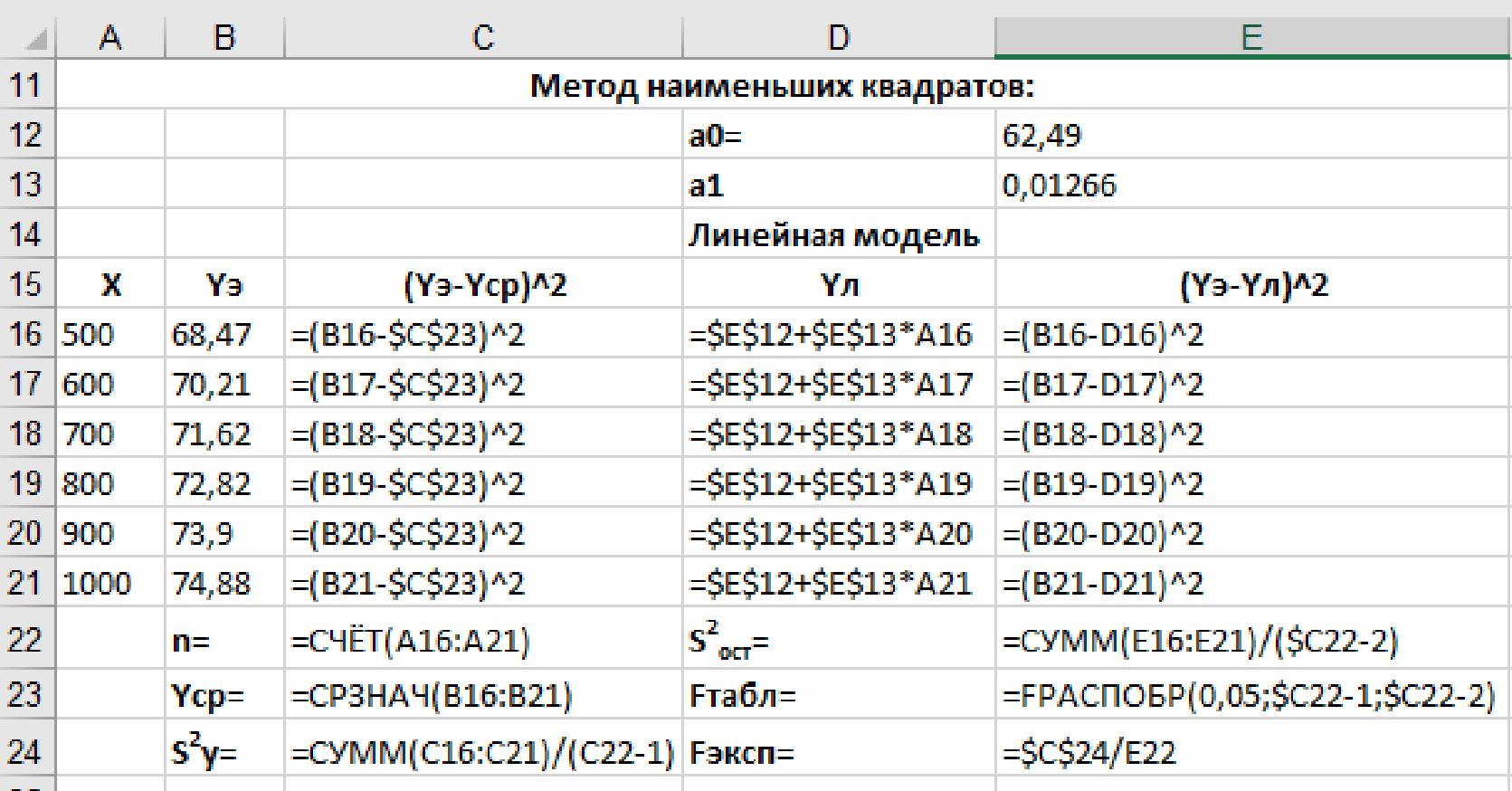 Выписать в журнал параметры линейной и квадратичной моделей эмпирических зависимостей теплоемкости вещества от температуры в заданном температурном интервале, а также результаты проверки адекватности полученных моделей. Сделать вывод о применимости линейной и квадратичной моделей для решения данной задачи. Отчет о выполнении работы • вариант задания, название соли; • формулы и параметры линейной теплоемкости вещества от температуры в заданном температурном интервале; • формулы для расчета дисперсии относительно среднего Sy, остаточных дисперсий Sост, критерия Фишера для линейной и квадратичной моделей; • результаты проверки адекватности полученных моделей (значения R2, табличные и экспериментальные значения критерия Фишера) и вывод о применимости линейной и квадратичной моделей для решения данной задачи; • схематичный график температурной зависимости теплоемкости вещества в заданном температурном диапазоне. 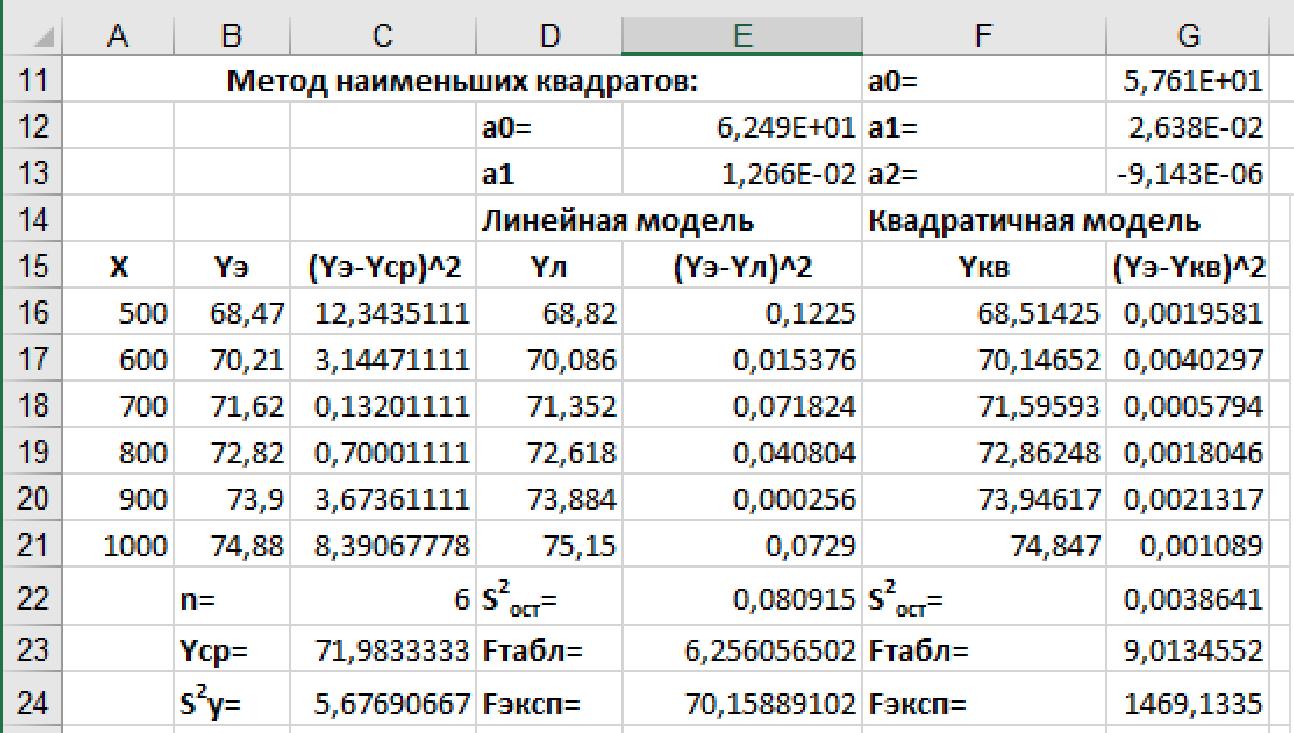 и квадратичной моделей эмпирических зависимостей Контрольные вопросы 1. В чем отличие постановки задачи регрессионного анализа от задачи интерполяции? 2. Является ли функция f(x)=a0+a1x+a2 x2+a3 x3 линейной по параметрам? 3. Могут ли регрессионные коэффициенты иметь отрицательные значения? 4. Приведите пример набора данных и линейной регрессионной модели f(x)=a0+a1x, где коэффициент a0 отрицательный, а коэффициент a1 положительный. 5. Для чего используется построение линии тренда? 6. Для чего необходимо изменять формат чисел – коэффициентов регрессионной модели? 7. При построении квадратичной модели коэффициент при х2 очень близок к нулю. Какая особенность экспериментальных данных может привести к такому результату? 8. Какие свойства экспериментальных данных характеризует дисперсия относительно среднего значения? Приведите пример набора данных, в которых эта дисперсия велика. 9. Приведите пример наборов данных и регрессионной модели, для которых дисперсия относительно среднего близка к остаточной дисперсии. 10. Приведите примеры наборов данных и регрессионных моделей, в которых остаточная дисперсия мала. 11. Что понимается под адекватностью регрессионной модели? Как оценить адекватность? 12. В каких пределах может изменяться коэффициент детерминированности? 13. Может ли значение остаточной дисперсии быть отрицательным? Почему? 14. Может ли значение критерия Фишера быть отрицательным? Почему? | |||||||||||||||||||||||||||||||||||||||||||||||
