Пр_4. Практическая работа Строгие методы сортировки и их реализация. Улучшенные методы сортировки и их реализация

• Название: Практическая работа Строгие методы сортировки и их реализация. Улучшенные методы сортировки и их реализация
• Дата: 16.11.2022
• Размер: 426.64 Kb.
• Имя файла: Пр_4.docx
• Тип: Практическая работа; #791108
• страница: 2 из 3

Сортировка слиянием

Алгоритм сортировки слиянием был изобретен Джоном фон Нейманом в 1945 году. Он является одним из самых быстрых способов сортировки.

Слияние – это объединение двух или более упорядоченных массивов в один упорядоченный.

Сортировка слиянием является одним из самых простых алгоритмов сортировки (среди быстрых алгоритмов). Особенностью этого алгоритма является то, что он работает с элементами массива преимущественно последовательно, благодаря чему именно этот алгоритм используется при сортировке в системах с различными аппаратными ограничениями (например, при сортировке данных на жестком диске). Кроме того, сортировка слиянием является алгоритмом, который может быть эффективно использован для сортировки таких структур данных, как связанные списки.

Данный алгоритм применяется тогда, когда есть возможность использовать для хранения промежуточных результатов память, сравнимую с размером исходного массива. Он построен на принципе "разделяй и властвуй". Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Далее их решения комбинируются, и получается решение исходной задачи ( рис. 4).

Процедура слияния требует два отсортированных массива. Заметим, что массив из одного элемента по определению является отсортированным.

Алгоритм сортировки слиянием

Шаг 1. Разбить имеющиеся элементы массива на пары и осуществить слияние элементов каждой пары, получив отсортированные цепочки длины 2 (кроме, быть может, одного элемента, для которого не нашлось пары).

Шаг 2. Разбить имеющиеся отсортированные цепочки на пары, и осуществить слияние цепочек каждой пары.

Шаг 3. Если число отсортированных цепочек больше единицы, перейти к шагу 2.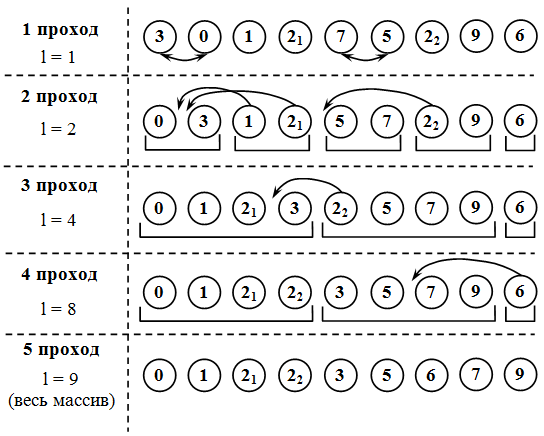



Рис. 4. Демонстрация сортировки слиянием по неубыванию
//Описание функции сортировки слиянием

void Merging_Sort (int n, int *x){

int i, j, k, t, s, Fin1, Fin2;

int* tmp = new int[n];

k = 1;

while (k < n){

t = 0;

s = 0;

while (t+k < n){

Fin1 = t+k;

Fin2 = (t+2*k < n ? t+2*k : n);

i = t;

j = Fin1;

for ( ; i < Fin1 && j < Fin2 ; s++){

if (x[i] < x[j]) {

tmp[s] = x[i];

i++;

}

else {

tmp[s] = x[j];

j++;

}

}

for ( ; i < Fin1; i++, s++)

tmp[s] = x[i];

for ( ; j < Fin2; j++, s++)

tmp[s] = x[j];

t = Fin2;

}

k *= 2;

for (s = 0; s < t; s++)

x[s] = tmp[s];

}

delete(tmp);

}

Недостаток алгоритма заключается в том, что он требует дополнительную память размером порядка n (для хранения вспомогательного массива). Кроме того, он не гарантирует сохранение порядка элементов с одинаковыми значениями. Но его временная сложность всегда пропорциональна O(n log n).
Улучшенные методы сортировки и их реализация
Цель: изучить основные алгоритмы внешних сортировок, научиться решать задачи сортировок массивов различными методами и выполнять оценку эффективности алгоритмов внешней сортировки.
Теоретическая часть
Внешние сортировки применяются к данным, которые хранятся во внешней памяти. При выполнении таких сортировок требуется работать с данными, расположенными на внешних устройствах последовательного доступа. Для файлов, расположенных на таких устройствах в каждый момент времени доступен только один компонент последовательности данных, что является существенным ограничением по сравнению с сортировкой массивов, где всегда доступен каждый элемент.

Внешняя сортировка – это сортировка данных, которые расположены на внешних устройствах и не вмещающихся в оперативную память.

Данные, хранящиеся на внешних устройствах, имеют большой объем, что не позволяет их целиком переместить в оперативную память, отсортировать с использованием одного из алгоритмов внутренней сортировки, а затем вернуть их на внешнее устройство. В этом случае осуществлялось бы минимальное количество проходов через файл, то есть было бы однократное чтение и однократная запись данных. Однако на практике приходится осуществлять чтение, обработку и запись данных в файл по блокам, размер которых зависит от операционной системы и имеющегося объема оперативной памяти, что приводит к увеличению числа проходов через файл и заметному снижению скорости сортировки.

К наиболее известным алгоритмам внешних сортировок относятся:

• 
  сортировки слиянием (простое слияние и естественное слияние);
  
• 
  улучшенные сортировки (многофазная сортировка и каскадная сортировка).
  

Из представленных внешних сортировок наиболее важным является метод сортировки с помощью слияния. Прежде чем описывать алгоритм сортировки слиянием введем несколько определений.

Основным понятием при использовании внешней сортировки является понятие серии. Серия (упорядоченный отрезок) – это последовательность элементов, которая упорядочена по ключу.

Количество элементов в серии называется длиной серии. Серия, состоящая из одного элемента, упорядочена всегда. Последняя серия может иметь длину меньшую, чем остальные серии файлов. Максимальное количество серий в файле N (все элементы не упорядочены). Минимальное количество серий одна (все элементы упорядочены).

В основе большинства методов внешних сортировок лежит процедура слияния и процедура распределения. Слияние – это процесс объединения двух (или более) упорядоченных серий в одну упорядоченную последовательность при помощи циклического выбора элементов, доступных в данный момент. Распределение – это процесс разделения упорядоченных серий на два и несколько вспомогательных файла.

Фаза – это действия по однократной обработке всей последовательности элементов. Двухфазная сортировка – это сортировка, в которой отдельно реализуется две фазы: распределение и слияние. Однофазная сортировка – это сортировка, в которой объединены фазы распределения и слияния в одну.

Двухпутевым слиянием называется сортировка, в которой данные распределяются на два вспомогательных файла. Многопутевым слиянием называется сортировка, в которой данные распределяются на N (N > 2) вспомогательных файлов.

Общий алгоритм сортировки слиянием

Сначала серии распределяются на два или более вспомогательных файлов. Данное распределение идет поочередно: первая серия записывается в первый вспомогательный файл, вторая – во второй и так далее до последнего вспомогательного файла. Затем опять запись серии начинается в первый вспомогательный файл. После распределения всех серий, они объединяются в более длинные упорядоченные отрезки, то есть из каждого вспомогательного файла берется по одной серии, которые сливаются. Если в каком-то файле серия заканчивается, то переход к следующей серии не осуществляется. В зависимости от вида сортировки сформированная более длинная упорядоченная серия записывается либо в исходный файл, либо в один из вспомогательных файлов. После того как все серии из всех вспомогательных файлов объединены в новые серии, потом опять начинается их распределение. И так до тех пор, пока все данные не будут отсортированы.

Выделим основные характеристики сортировки слиянием:

• 
  количество фаз в реализации сортировки;
  
• 
  количество вспомогательных файлов, на которые распределяются серии.
  

Рассмотрим основные и наиболее важные алгоритмы внешних сортировок более подробно.

Сортировка простым слиянием

Одна из сортировок на основе слияния называется простым слиянием.

Алгоритм сортировки простым слияния является простейшим алгоритмом внешней сортировки, основанный на процедуре слияния серией.

В данном алгоритме длина серий фиксируется на каждом шаге. В исходном файле все серии имеют длину 1, после первого шага она равна 2, после второго – 4, после третьего – 8, после k -го шага – 2^k.

Алгоритм сортировки простым слиянием

Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2.

Шаг 2. Вспомогательные файлы f1 и f2 сливаются в файл f, при этом одиночные элементы образуют упорядоченные пары.

Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2. При этом упорядоченные пары переходят в упорядоченные четверки.

Шаг 4. Повторяя шаги, сливаем четверки в восьмерки и т.д., каждый раз удваивая длину слитых последовательностей до тех пор, пока не будет упорядочен целиком весь файл ( рис. 1).

После выполнения i проходов получаем два файла, состоящих из серий длины 2ⁱ. Окончание процесса происходит при выполнении условия 2ⁱ>=n. Следовательно, процесс сортировки простым слиянием требует порядка O(log n) проходов по данным.

Признаками конца сортировки простым слиянием являются следующие условия:

• 
  длина серии не меньше количества элементов в файле (определяется после фазы слияния);
  
• 
  количество серий равно 1 (определяется на фазе слияния).
  
• 
  при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.
  

Рис. 1. Демонстрация сортировки двухпутевым двухфазным простым слиянием


//Описание функции сортировки простым слиянием

void Simple_Merging_Sort (char *name){

int a1, a2, k, i, j, kol, tmp;

FILE *f, *f1, *f2;

kol = 0;

if ( (f = fopen(name,"r")) == NULL )

printf("\nИсходный файл не может быть прочитан...");

else {

while ( !feof(f) ) {

fscanf(f,"%d",&a1);

kol++;

}

fclose(f);

}

k = 1;

while ( k < kol ){

f = fopen(name,"r");

f1 = fopen("smsort_1","w");

f2 = fopen("smsort_2","w");

if ( !feof(f) ) fscanf(f,"%d",&a1);

while ( !feof(f) ){

for ( i = 0; i < k && !feof(f) ; i++ ){

fprintf(f1,"%d ",a1);

fscanf(f,"%d",&a1);

}

for ( j = 0; j < k && !feof(f) ; j++ ){

fprintf(f2,"%d ",a1);

fscanf(f,"%d",&a1);

}

}

fclose(f2);

fclose(f1);

fclose(f);
f = fopen(name,"w");

f1 = fopen("smsort_1","r");

f2 = fopen("smsort_2","r");

if ( !feof(f1) ) fscanf(f1,"%d",&a1);

if ( !feof(f2) ) fscanf(f2,"%d",&a2);

while ( !feof(f1) && !feof(f2) ){

i = 0;

j = 0;

while ( i < k && j < k && !feof(f1) && !feof(f2) ) {

if ( a1 < a2 ) {

fprintf(f,"%d ",a1);

fscanf(f1,"%d",&a1);

i++;

}

else {

fprintf(f,"%d ",a2);

fscanf(f2,"%d",&a2);

j++;

}

}

while ( i < k && !feof(f1) ) {

fprintf(f,"%d ",a1);

fscanf(f1,"%d",&a1);

i++;

}

while ( j < k && !feof(f2) ) {

fprintf(f,"%d ",a2);

fscanf(f2,"%d",&a2);

j++;

}

}

while ( !feof(f1) ) {

fprintf(f,"%d ",a1);

fscanf(f1,"%d",&a1);

}

while ( !feof(f2) ) {

fprintf(f,"%d ",a2);

fscanf(f2,"%d",&a2);

}

fclose(f2);

fclose(f1);

fclose(f);

k *= 2;

}

remove("smsort_1");

remove("smsort_2");

}

Листинг .

Заметим, что для выполнения внешней сортировки методом простого слияния в оперативной памяти требуется расположить всего лишь две переменные – для размещения очередных элементов (записей) из вспомогательных файлов. Исходный и вспомогательные файлы будут O(log n) раз прочитаны и столько же раз записаны.

Сортировка естественным слиянием

В случае простого слияния частичная упорядоченность сортируемых данных не дает никакого преимущества. Это объясняется тем, что на каждом проходе сливаются серии фиксированной длины. При естественном слиянии длина серий не ограничивается, а определяется количеством элементов в уже упорядоченных подпоследовательностях, выделяемых на каждом проходе.

Сортировка, при которой всегда сливаются две самые длинные из возможных последовательностей, является естественным слиянием. В данной сортировке объединяются серии максимальной длины.

Алгоритм сортировки естественным слиянием

Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2. Распределение происходит следующим образом: поочередно считываются записи a_i исходной последовательности (неупорядоченной) таким образом, что если значения ключей соседних записей удовлетворяют условию f(a_i)<=f(a_i+1), то они записываются в первый вспомогательный файл f1. Как только встречаются f(a_i)>f(a_i+1), то записи a_i+1 копируются во второй вспомогательный файл f2. Процедура повторяется до тех пор, пока все записи исходной последовательности не будут распределены по файлам.

Шаг 2. Вспомогательные файлы f1 и f2 сливаются в файл f, при этом серии образуют упорядоченные последовательности.

Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2.

Шаг 4. Повторяя шаги, сливаем упорядоченные серии до тех пор, пока не будет упорядочен целиком весь файл.

Символ "`" обозначает признак конца серии.

Признаками конца сортировки естественным слиянием являются следующие условия:

• 
  количество серий равно 1 (определяется на фазе слияния).
  
• 
  при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.
  

Естественное слияние, у которого после фазы распределения количество серий во вспомогательных файлах отличается друг от друга не более чем на единицу, называется сбалансированным слиянием, в противном случае – несбалансированное слияние.



Рис. 2. Демонстрация сортировки двухпутевым двухфазным естественным слиянием
//Описание функции сортировки естественным слиянием

void Natural_Merging_Sort (char *name){

int s1, s2, a1, a2, mark;

FILE *f, *f1, *f2;

s1 = s2 = 1;

while ( s1 > 0 && s2 > 0 ){

mark = 1;

s1 = 0;

s2 = 0;

f = fopen(name,"r");

f1 = fopen("nmsort_1","w");

f2 = fopen("nmsort_2","w");

fscanf(f,"%d",&a1);

if ( !feof(f) ) {

fprintf(f1,"%d ",a1);

}

if ( !feof(f) ) fscanf(f,"%d",&a2);

while ( !feof(f) ){

if ( a2 < a1 ) {

switch (mark) {

case 1:{fprintf(f1,"' "); mark = 2; s1++; break;}

case 2:{fprintf(f2,"' "); mark = 1; s2++; break;}

}

}

if ( mark == 1 ) { fprintf(f1,"%d ",a2); s1++; }

else { fprintf(f2,"%d ",a2); s2++;}

a1 = a2;

fscanf(f,"%d",&a2);

}

if ( s2 > 0 && mark == 2 ) { fprintf(f2,"'");}

if ( s1 > 0 && mark == 1 ) { fprintf(f1,"'");}

fclose(f2);

fclose(f1);

fclose(f);

cout << endl;

Print_File(name);

Print_File("nmsort_1");

Print_File("nmsort_2");

cout << endl;

f = fopen(name,"w");

f1 = fopen("nmsort_1","r");

f2 = fopen("nmsort_2","r");

if ( !feof(f1) ) fscanf(f1,"%d",&a1);

if ( !feof(f2) ) fscanf(f2,"%d",&a2);

bool file1, file2;

while ( !feof(f1) && !feof(f2) ){

file1 = file2 = false;

while ( !file1 && !file2 ) {

if ( a1 <= a2 ) {

fprintf(f,"%d ",a1);

file1 = End_Range(f1);

fscanf(f1,"%d",&a1);

}

else {

fprintf(f,"%d ",a2);

file2 = End_Range(f2);

fscanf(f2,"%d",&a2);

}

}

while ( !file1 ) {

fprintf(f,"%d ",a1);

file1 = End_Range(f1);

fscanf(f1,"%d",&a1);

}

while ( !file2 ) {

fprintf(f,"%d ",a2);

file2 = End_Range(f2);

fscanf(f2,"%d",&a2);

}

}

file1 = file2 = false;

while ( !file1 && !feof(f1) ) {

fprintf(f,"%d ",a1);

file1 = End_Range(f1);

fscanf(f1,"%d",&a1);

}

while ( !file2 && !feof(f2) ) {

fprintf(f,"%d ",a2);

file2 = End_Range(f2);

fscanf(f2,"%d",&a2);

}

fclose(f2);

fclose(f1);

fclose(f);

}

remove("nmsort_1");

remove("nmsort_2");

}

//определение конца блока

bool End_Range (FILE * f){

int tmp;

tmp = fgetc(f);

tmp = fgetc(f);

if (tmp != '\'') fseek(f,-2,1);

else fseek(f,1,1);

return tmp == '\'' ? true : false;

}

Листинг .

Таким образом, число чтений или перезаписей файлов при использовании метода естественного слияния будет не хуже, чем при применении метода простого слияния, а в среднем – даже лучше. Но в этом методе увеличивается число сравнений за счет тех, которые требуются для распознавания концов серий. Помимо этого, максимальный размер вспомогательных файлов может быть близок к размеру исходного файла, так как длина серий может быть произвольной.
Ключевые термины

Алгоритм сортировки – это алгоритм для упорядочения некоторого множества элементов.

Бинарная пирамидальная сортировка – это алгоритм внутренней сортировки, основанный на построении пирамиды и просеивании элементов из ее вершины методом спуска вниз в соответствии с ключом сортировки.

Быстрая сортировка – это общее название ряда алгоритмов, которые отражают различные подходы к получению критичного параметра, влияющего на производительность метода.

Внешняя сортировка – это алгоритм сортировки, который при проведении упорядочивания данных использует внешнюю память, как правило, жесткие диски.

Внутренняя сортировка – это алгоритм сортировки, который в процессе упорядочивания данных использует только оперативную память (ОЗУ) компьютера.

Время сортировки – основной параметр трудоемкости алгоритма, характеризующий быстродействие алгоритма сортировки.