Метрология МГРИ практическая 1. метрология практическая 1 (1). Практическая работа 1 Измерение физической величины. Математическая обработка результатов измерений
 Скачать 0.76 Mb.
|
|
Бунаков Сергей РТБ-17 Вариант №2 Практическая работа №1 Измерение физической величины. Математическая обработка результатов измерений. Цель работы: приобретений практических навыков обработки результатов измерений. Порядок выполнения работы 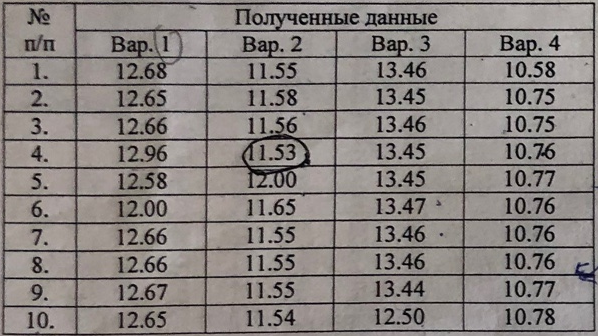 Полученные данные обрабатывают в следующей последовательности. Исключаем грубые погрешности(промахи) Для этого располагаем измерения в порядке возрастания и определяем “выскакивающие” величины, наибольшие и наименьшие. Если величина имеет наибольшее крайнее значение, то составляют по 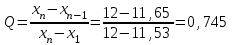 Где числитель – разность между предполагаемыми крайним “выскакивающим значением и значением, которое ему предшествует. Знаменатель - разность между наибольшим и наименьшим значением измерений. Вычисленную величину “Q” оцениваем с помощью табличного зачения которое выбирают в соответствии с выбранным значение уровня значимости числа измерений “n”. Наличие “ выскакивающего” значения будет доказано, если “Q” вычисленное будет больше, чем табличное значение “Q” 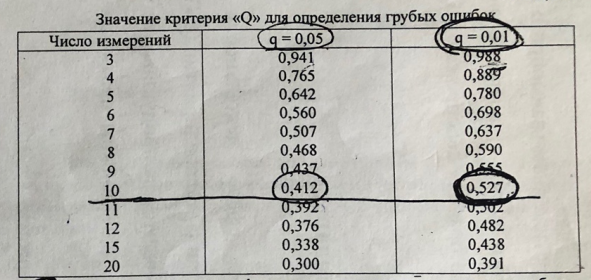 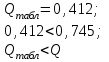 Следовательно, наличие “ выскакивающего” значения доказано. 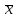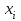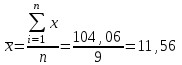Определяем среднее арифметическое значение  результатов наблюдения   Где 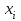- значение параметра в отдельном опыте;n- число измерений. Определяем отклонение для среднего значения для каждого результата ( 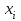- 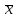) и полученное отклонение возводят в квадрат. Полученные результаты заносят в таблицу
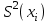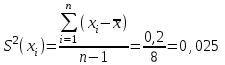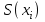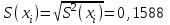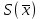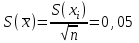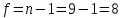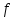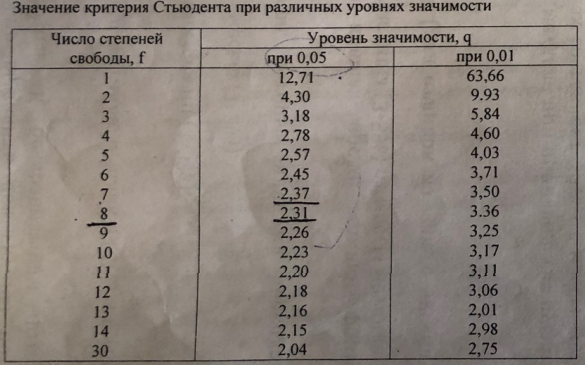Вычисляем экспериментальную оценку дисперсии воспроизводимости   Вычисляем экспериментальную оценку стандартного отклонения отдельного определения   Вычисляем экспериментальную оценку стандартного отклонения среднего результата   Получаем надёжность полученных результатов по критерию Стьюдента t α при избранной доверительной вероятности α (0,95)   - число свободных степеней По таблице находим критерий Стьюдента t α = 2,31 Теперь рассчитываем ошибку полученного среднего результата 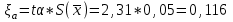 Устанавливаем интервал в котором с выбранной доверительной вероятностью α находится средний результат 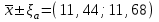 Определяем относительную ошибку 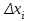 , % 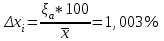Относительная ошибка меньшие 10% значит грубые ошибки полностью исключены. Ответы на контрольные вопросы 1)Что такое измерение? Измерение – это определение значений физической величины опытным путём с помощью специально предназначенных для этого технических средств. 2)Классификация измерений по видам и методам? По видам измерения делятся на прямые, косвенные, совокупные, совместные. Методы измерения: непосредственной оценки, сравнение с мерой, противопоставление, замещения, нулевой, дифференциальный, перестановки, дополнения, совпадения. 3)Приведите классификацию средств измерений? Все средства измерений подразделяются на меры, измерительные преобразователи, измерительные приборы, измерительные установки и системы. 4)Что называется метрологическими характеристиками средств измерений? Технические средства, которые используют при измерениях и имеют нормированные метрологические характеристики, называют средствами измерений. 5)Что понимают под классом точности средств измерений? Под классом точности средств измерения понимается такая обобщённая характеристика, которая определяется пределами допускаемы основные и дополнительных погрешностей, а также другими свойствами измерений, влияющих на точность измерений. 6)Как обозначаются класс точности измерительных приборов? Обозначение класса точности прибора наносится а циферблаты, щитки и корпуса средств измерений, приводятся в нормативных документах и могут быть представлены в различном виде. 7) Приведите последовательность обработки экспериментальных данных. Для получения оценки измеряемой величины максимально близкой к истинному значению необходимо по экспериментальным данным выявить и исключить промахи найти оценку математического ожидания отдельных результатов наблюдений оценить систематическую погрешность и исключить её из оценки математического ожидания. 8) Что такое промахи и грубые погрешности? Грубые погрешности (промахи) обычно обусловлены неправильным отсчетом по шкале прибора, ошибкой при записи наблюдений, наличием сильно влияющей величины, неисправностью средств измерений и другими причинами. При однократных измерениях обнаружить промах не представляется возможным. Каков порядок исключения грубых погрешностей? Для этого располагаем измерения в порядке возрастания и определяем “выскакивающие” величины, наибольшие и наименьшие. Вычисленную величину “Q” оцениваем с помощью табличного значения которое выбирают в соответствии с выбранным значение уровня значимости числа измерений “n”. Наличие “ выскакивающего” значения будет доказано, если “Q” вычисленное будет больше, чем табличное значение “Q” 10)Что такое систематическая погрешность? Систематическая погрешность — составляющая погрешности результата измерения, остающаяся постоянной (или же закономерно изменяющейся) при повторных измерениях одной и той же величины. 11)Как можно исключить систематические погрешности? Метод исключения систематической погрешности путем введения поправки в результат измерений применяют очень широко. |
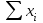=104,06
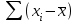= 0
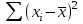= 0,2