Задачи по программе фарм. Тема 1 Измерение физических величин. Прямые и косвенные измерения. Ошибки и погрешности измерений физических величин. Прямые и косвенные измерения. Обработка результатов прямых измерений. Прямые измерения
 Скачать 5.58 Mb. Скачать 5.58 Mb.
|
|
Тема 1: Измерение физических величин. Прямые и косвенные измерения. Ошибки и погрешности измерений физических величин. Прямые и косвенные измерения. Обработка результатов прямых измерений. Прямые измерения Пример 1. При измерении штангенциркулем с погрешностью 𝛿=0,05 мм диаметра 𝐷 калиброванного цилиндра получены значения: 𝐷1=19,80 мм; 𝐷2=19,85 мм; 𝐷3=19,80 мм; 𝐷4=19,80 мм. Решение:  Пример 2. При измерении диаметра грубо обработанной детали микрометром, погрешность которого 𝛿=0,01 мм, получены следующие значения: 𝐷1=19,82 мм; 𝐷2=19,87 мм; 𝐷3=19,74 мм; 𝐷4=19,80 мм; 𝐷5=19,77 мм; 𝐷6=19,85 мм; 𝐷7=19,81 мм; 𝐷8=19,80 мм; 𝐷9=19,73 мм; 𝐷10=19,87 мм. Решение: Вычисляем: 2) СКО результата отдельного измерения 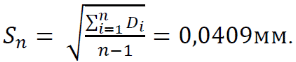 Рассчитываем доверительный интервал Δ𝐷, задаваясь определенным значением доверительной вероятности Р, например, Р = 0,95(95%). По таблице находим коэффициент Стьюдента 𝑡10;0,95=2,3. Тогда 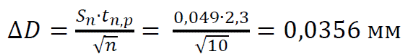 или, после округления , Δ𝐷≈0,04 мм. Соответственно округляем значение диаметра и записываем окончательный результат: 𝐷=(19,81±0,04)мм; 𝜀𝐷 =0,2%; Р = 0,95. Пример 3. При измерении мирового рекорда на спринтерской дистанции 100 м использовался электронный секундомер с относительной нструментальной погрешностью 0.2 %. Скажите, можно ли уверенно утверждать, что время 8.70 с является новым мировым рекордом, если время действующего мирового рекорда равно (8.745 ± 0.001) с ? Решение: 1) Найдем абсолютную погрешность измерения времени нового рекорда на дистанции 100 м: 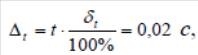 где δt – относительная погрешность, 0.2 %; t – значение физической величины, 8.70 с; Δt – абсолютная погрешность, с. 2) Результат измерения представим в виде интервала: (8.70 ± 0.02) с 3) Сравним результат с действующим рекордом: (8.745 ± 0.001) с 4) Время 8.70 с является новым мировым рекордом, так как выполняется неравенство: (8.745 – 0.001) c > (8.70 + 0.02) c 8.744 c > 8.72 c Пример. При измерении диаметра цилиндра в различных местах штангенциркулем получено одинаковое значение D = 12,5 мм. Абсолютная погрешность штангенциркуля 0,1 мм. Произведите оценку точности изме-рения. 1. Предельная абсолютная погрешность технического измерения равна абсолютной погрешности штангенциркуля Δxпр= 0,1 мм. 2. Предельная относительная погрешность технического измерения равна относительной погрешности штангенциркуля  3. Результат измерения следует записать так: D = (12,5 ± 0,1) мм. Косвенные измерения Пример 1. Определить абсолютную и относительную погрешности по единичным измерениям соответствующих аргументов коэффициента вязкости касторового масла, определенного методом Стокса. Величина коэффициента вязкости в этом случае определяется формулой: 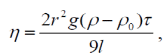 где r – радиус шарика, g – ускорение свободного падения, – плотность свинца, о – плотность касторового масла, l – расстояние пройденное шариком, – время движения шарика. В результате измерений были получены значения: l 0,75, измеренное с точностью до 0,005 м, r 2,0 10-3м, измеренное с точностью до 0,1 10-4м, 5,96 с, измеренное с точностью до 0,01 с, 10320 кг/м3, измеренное с точностью до 0,5 кг/м3 g 9,8м/с2, измеренное с точностью до 0,05 м/с2. Определим коэффициент вязкости, используя закон Стокса: 2. Логарифмируя выражение закона Стокса, получим: 3. Дифференцируем полученное выражение: 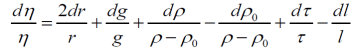 4. Заменяем знак дифференциала на знак приращения и находим макси-мальную относительную погрешность: 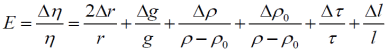 Так как , то 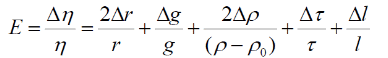 Подставляя численные значения, получим: В процентах относительная погрешность составляет: 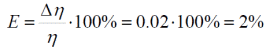 Максимально возможная абсолютная погрешность в определении вязко- сти равна: Результат измерений представим в виде: Пример 2. Найдите объем детали и его погрешность, если измерения ребер прямоугольного параллелепипеда дали результат: x = (58,3 ± 0,5) мм y = (14,2 ± 0,5) мм z = (44,4 ± 0,5) мм Решение: 1) Объем прямоугольного параллелепипеда определяется произведением длины, ширины и высоты: 2) Изменение объема dV при бесконечно малых приращениях размеров dx, dy, dz определяется полным дифференциалом функции V (x, y, z):  3) Перейдем от бесконечно малых приращений к определенным значениям случайных погрешностей: ΔV, Δx, Δy, Δz. 4) Вычислим частные производные: 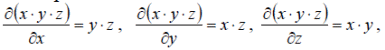 5) Для упрощения расчетов разделим обе части уравнения на квадрат объема 6) Найдем относительные погрешности: 7) Вычислим погрешность объема: 8) Вычислим абсолютную погрешность: 9) Перепишем результат с учетом погрешности измерения:   Тема 2: Геометрический и физический смысл производной. Нахождение производных. Производные высших порядков. Скорость как первая производная пути по времени. Ускорение как вторая производная пути по времени. Пример 1. Найти производную функции  Пример 2. Найти производную функции y 3cosx. Смотрим в таблицу производных. Производная косинуса там есть, но у нас 3cosx. Вычисляем: y3cos x выносим постоянный множитель за знак производной: y3cos x3 cos x Пользуемся таблицей производных: y3cosx3 cosx3sin x sin x. Пример 3. Найти производную функции Применяем правило производной суммы 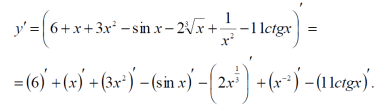 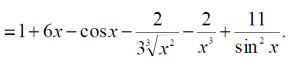 для дифференцирования все корни, степени нужно представить в виде Пример 4. Найти производную функции В этом примере дано произведение двух функций, зависящих от х. Применим правило умножения производных: Пример 5. Найти производную функции 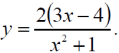 Применяем правило дифференцирования частного: 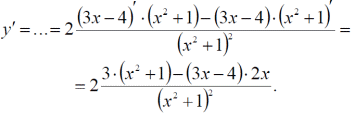 Пример 6. Найти производную сложной функции Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции (u(v))u(v) v: 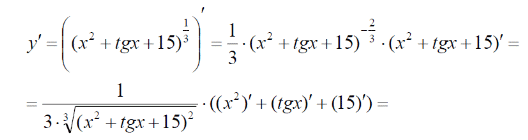 Пример 8. Путь при свободном падении тела определяется формулой S (t) gt2 . Найти скорость свободного падения. Решение. 1. Дадим моменту времени t приращение  t , получим момент (t + t , получим момент (t +  t). t).2. Вычислим 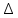 S : S : Пример 9. Путь, пройденный автомобилем зависит от времени по закону: Решение 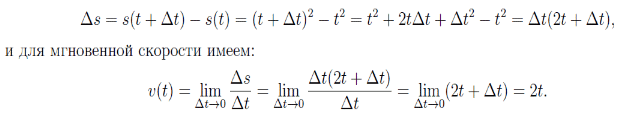 Для момента 3с имеем: Пример 10. Закон движения точки определяется заданием ее радиус вектора. Найти величину и направление ускорения движения точки в любой момент времени. Решение: Первая производная вектор-функции определяет вектор скорости движения точки . Вторая производная – вектор ускорения Величина ускорения Пример 11. 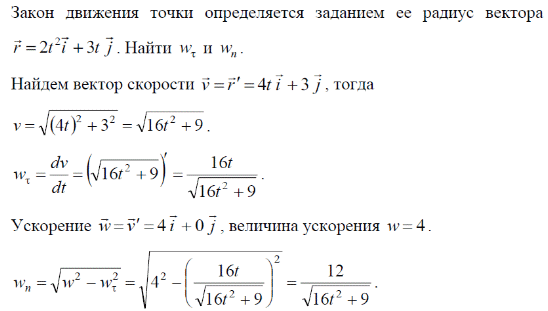 Производные высших порядков. Пример 7. Для примера возьмем квадратичную функцию f x, ax2bx c тогда первая производная f x2ax b, вторая производная f x2a, и третья производная f x0. Пример 9. Координата тела задана формулой: 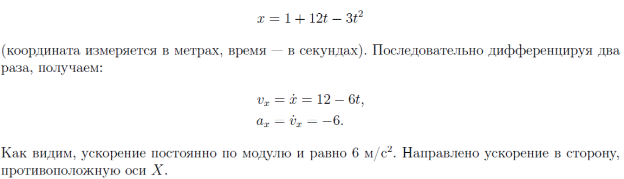 Пример 10. Рассмотрим экспоненциальную функцию f xe x Для первой производной имеем f xe x Легко сообразить, что в этом случае все производные более высокого порядка имеют такой же вид, т.е. e f xf xf xf x... Домашнее задание Найти производную функции 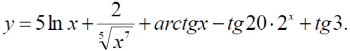 Найти производную функции Найти производную функции  Найти производную функции  Найти производную функции Найти производные указанных порядков: 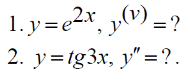 Определить скорость тела в момент времени t = 2 c, если его координата x изменяется по закону x= At3 (A = 2 м/с3), а координаты y и z не изменяются. При движении тела его координаты изменяются согласно уравнениям y(t)=0; z(t)=0; x(t)= At4 -Bt5 , где A=0,05 м/с4 иB=0,01 м/с5. Определить среднюю скорость перемещения, среднюю путевую скорость и среднее ускорение тела за промежуток времени 0 ÷ 6 с. Тема 3: Понятие дифференциала. Дифференциалы функции одной переменной. Частная производная и частный дифференциал. Полный дифференциал. Пример 1.Вычислить дифференциал функции y sin x. Ответ dy cos xdx . Пример 2.Вычислить дифференциал функции Ответ Пример 3.Вычислить дифференциал функции Решение 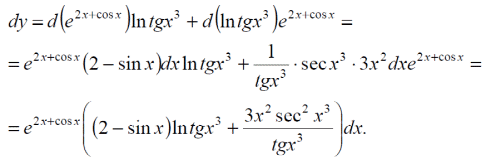 Пример 4.Применение дифференциала для приближенных вычислений.  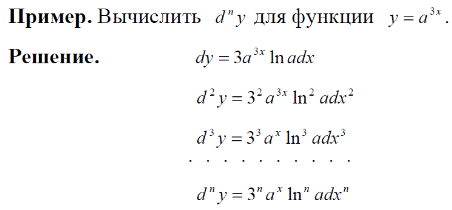 Домашнее задание Найти дифференциал функции:  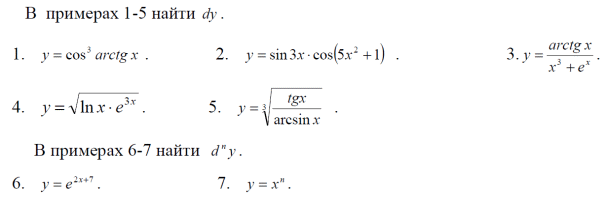 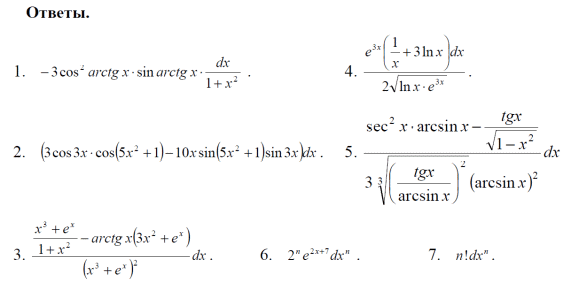 |
