Задачи по программе фарм. Тема 1 Измерение физических величин. Прямые и косвенные измерения. Ошибки и погрешности измерений физических величин. Прямые и косвенные измерения. Обработка результатов прямых измерений. Прямые измерения
 Скачать 5.58 Mb. Скачать 5.58 Mb.
|
|
Тема 7. Реологическое свойство материалов - упругость. Законы упругой деформации. Простейшие реологические модели абсолютно: упругих, вязких, пластических тел. Тема 8. Простейшие реологические модели. Простейшие реологические модели: упруговязкая система (модель Максвелла); вязкоупругая система (модель Кельвина-Фойгта); вязкопластическая система (модель Бингама). Релаксация механического напряжения, ползучесть. Тема 9. Гармонические колебания. Кинематика колебаний. Гармонические колебания. Уравнение гармонических колебаний (дифференциальное уравнение гармонических колебаний и его решение); скорость и ускорение при гармоническом колебательном движении. Пример 1. Через какое минимальное время t , считая от начала колебаний, смещение колеблющейся материальной точки составит половину амплитуды? Период колебаний T = 24 с. Найти среднюю скорость точки u ср за это время. Амплитуда колебаний A= 0,1 м. Решение. Обозначим a0 начальную фазу колебаний, x - смещение колеблющейся точки. Поскольку в условии задачи идет речь о смещении x и амплитуде A колеблющейся точки, запишем уравнение гармонических колебаний точки, в которое входят обе эти величины (с учетом, что a0 = 0): x Acost .   Пример 2. Гармонические колебания величины s описываются уравнением 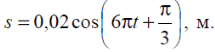 Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний. Уравнение гармонических колебаний имеет вид s = Acos( 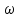 0t + 0t + 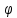 ). Сравнивая его с данным, имеем ). Сравнивая его с данным, имеем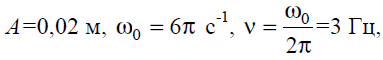 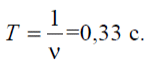 Пример 3. Материальная точка совершает гармонические колебания с амплитудой A=4 см и периодом T =2 с. Напишите урав- нение движения точки, если ее движение начинается из положения x0=2 см. 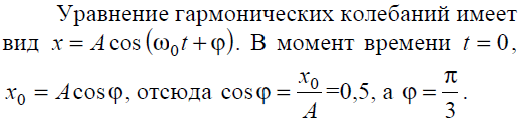 В результате уравнение движения точки будет иметь вид 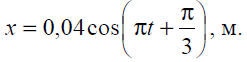 Пример 4. Материальная точка совершает гармонические колебания согласно уравнению 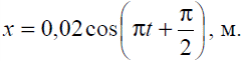 Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки. 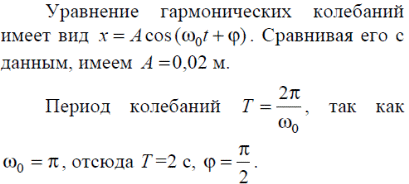 Скорость есть первая производная от перемещения по времени, а ускорение вторая соответственно, откуда 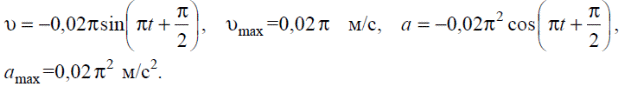 Пример 5. Точка совершает гармонические колебания по закону х = Asin(  t + t + ). ).Наибольшее смещение x max = 100см, наибольшая скорость vmax = 20м/с. Найти уравнение гармонических колебаний и максимальное ускорение точки. Решение. Из условия и последующего дифференцирования имеем 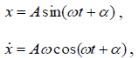 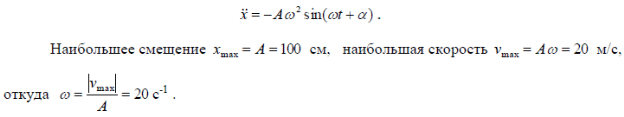 Тогда уравнение гармонических колебаний будет 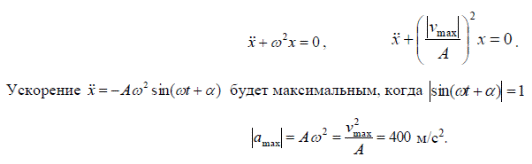 Пример 6. На горизонтальной пружине жесткостью k = 800 Н м укреплен груз массой M = 4 кг, лежащий на гладкой горизонтальной поверхности. Другой конец пружины прикреплён к вертикальной стене. Пуля массой m =10 г , летящая с горизонтальной скоростью v0 = 600 м/ с , попадает в тело и застревает в нём. Пренебрегая массой пружины и сопротивлением воздуха, определить: 1) период колебаний тела; 2) амплитуду колебаний тела. Решение Уравнение гармонических колебаний примет вид где собственная частота 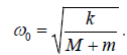 Тогда период малых колебаний системы равен . 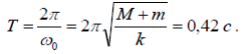 Запишем закон сохранения импульса 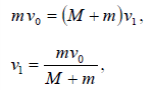 здесь v1– скорость, с которой будет двигаться система груз – пуля после взаимодействия. Решение уравнения гармонических колебаний есть 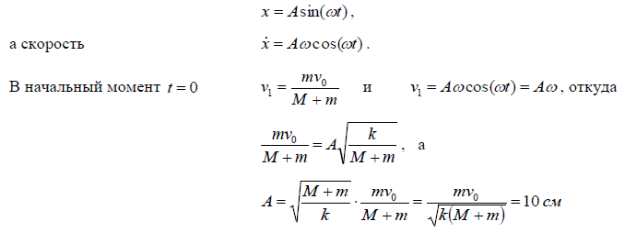  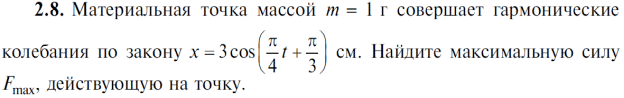 Тема 10. Механические волны. Характеристики волновых процессов. Динамика распространения колебаний в упругой среде. ДУ уравнение волны. Скорость распространения волны в упругой среде.  Пример 1.   Пример 2. Волна распространяется в упругой среде со скоростью 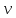 = 200 м/с. Определите наименьшее расстояние между точками среды, совершающими колебания в противоположных фазах, если частота = 200 м/с. Определите наименьшее расстояние между точками среды, совершающими колебания в противоположных фазах, если частота 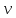 колебаний равна 50 Гц. колебаний равна 50 Гц.Решение Расстояние между ближайшими точками среды, совершающими колебания в противоположных фазах, равно 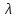 /2. Следовательно, x = /2. Следовательно, x = 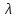 / 2. Учитывая связь между длиной волны / 2. Учитывая связь между длиной волны 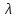 и частотой и частотой 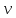 , ,x = 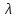 / 2, / 2,где 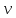 - скорость распространения колебаний в среде, получаем искомое расстояние - скорость распространения колебаний в среде, получаем искомое расстояниеВычисляя, получаем x=2 м. Пример 3. Волна распространяется в упругой среде со скоростью 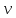 = 150 м/с с частотой = 150 м/с с частотой 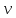 = 100 Гц. Определите разность фаз = 100 Гц. Определите разность фаз 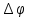 колебаний двух точек среды, лежащих на луче и отстоящих друг от друга на расстоянии колебаний двух точек среды, лежащих на луче и отстоящих друг от друга на расстоянии 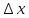 = 0,75 м. = 0,75 м.Решение Если две точки среды отстоят друг от друга на расстоянии, равном длине волны 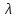 , то разность фаз равна 2 , то разность фаз равна 2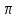 . Следовательно, если две точки среды отстоят друг от друга на . Следовательно, если две точки среды отстоят друг от друга на 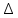 x , то разность фаз x , то разность фаз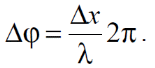 Длина волны найдем искомую разность фаз 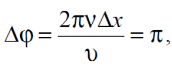 т.е. точки среды колеблются в противофазе. Пример 4. Определите, во сколько раз изменится длина звуковой волны при переходе звука из воды в воздух, если принять скорость звука в воздухе  1= 330 м/с, в воде 1= 330 м/с, в воде  2= 1450 м/с. 2= 1450 м/с.Решение При переходе из одной среды в другую частота колебаний не изменяется (она зависит только от свойств источника волн), т. е.   Пример 5. 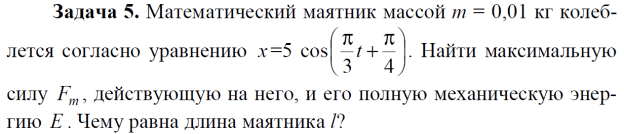  Одну величину мы нашли. Теперь найдем полную механическую энергию маятника E . По закону сохранения механической энергии она равна его максимальной кинетической энергии Tm : 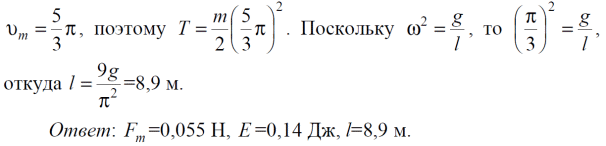 Пример 6. Материальная точка колеблется согласно уравнению x = Acoswt , где A=5 см и 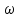 = π/12 с-1. Возвращающая сила F в = π/12 с-1. Возвращающая сила F впервый раз достигает значения 12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите этот момент времени t ;  Ответ: Пример 7. Во сколько раз уменьшится период колебаний шарика на резиновом подвесе, если его укоротить, отрезав 75% его длины? Обозначим 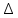 l = l1 - l2 изменение длины подвеса, l1- первоначальную и l2 - конечную длины, T1- период колебаний шарика длине l1, T2 - период его колебаний после укорочения подвеса. l = l1 - l2 изменение длины подвеса, l1- первоначальную и l2 - конечную длины, T1- период колебаний шарика длине l1, T2 - период его колебаний после укорочения подвеса. 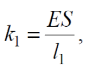 где E - модуль Юнга (модуль упругости) резины и S – площадь поперечного сечения подвеса. 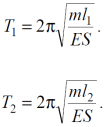 Чтобы исключить из решения неизвестные параметры m, E и S и ответить на вопрос задачи, найдем отношение 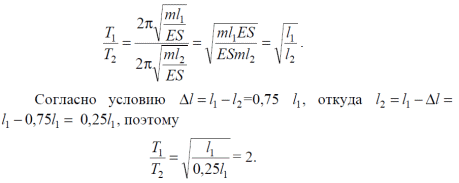 Домашнее задание Волна распространяется в упругой среде вдоль положительного направления оси х. Запишите уравнение волны посредством известных следующих параметров: амплитуда волны А, скорость волны 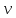 и длина волны и длина волны 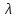 . .Источником плоской волны является вибратор, колеблющийся по закону x = 0,2cos20πt , м. Скорость распространения колебаний в среде 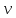 = 30 м/с. Запишите уравнение плоской волны, распространяющейся вдоль прямой, совпадающей с положительным направлением оси х в среде. = 30 м/с. Запишите уравнение плоской волны, распространяющейся вдоль прямой, совпадающей с положительным направлением оси х в среде.Плоская синусоидальная волна распространяется вдоль прямой, совпадающей с положительным направлением оси х в среде, не поглощающей энергию, со скоростью 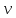 = 15 м/с. Две точки, находящиеся на этой прямой на расстояниях x1=5 м и x2= 5,5 м от источника колебаний, колеблются с разностью фаз = 15 м/с. Две точки, находящиеся на этой прямой на расстояниях x1=5 м и x2= 5,5 м от источника колебаний, колеблются с разностью фаз 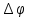 = π/5. Амплитуда волны А = 4 см. Определите: длину волны; уравнение волны; смещение первой точки в момент времени t = 3 c. = π/5. Амплитуда волны А = 4 см. Определите: длину волны; уравнение волны; смещение первой точки в момент времени t = 3 c.Тема 11. Звук. Ультразвук. Физические характеристики звука. Вектор Умова. Порог слышимости, зависимость от частоты. Закон Вебера- Фехнера. Ультразвук и его действия на вещество, применительно к задачам фармации. Пример 1. Два звука отличаются по уровню громкости на Г = 5 фон. Определите отношение интенсивностей этих звуков. 1 фон - громкость для звука стандартной частоты 1000 Гц [частота стандартного тона (синусоидального акустического колебания)], если его уровень интенсивности равен 1 дБ. Следовательно, Г= 5 фон соответствует уровень интенсивности звука Г= 5 дБ = 0,5 Б. Уровень интенсивности звука 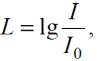 где I0 - интенсивность звука на пороге слышимости, принимаемая для всех звуков равной 10 пВт/м2 . 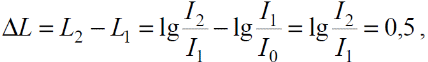 откуда искомое отношение интенсивности звуков 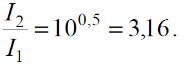 Пример 2. Звуковые колебания, имеющие частоту =500 Гц и амплитуду A=0,25 мм, распространяются в воздухе. Длина волны =70 см. Найти скорость распространения колебаний (т.е. скорость волны) и максимальную скорость колебаний частиц воздуха m. Скорость волны мы можем определить сразу, воспользовавшись формулой, устанавливающей связь длины волны с частотой колебаний v частиц в ней: 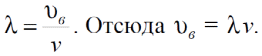 Чтобы найти максимальную скорость частиц в волне m , надо взять первую производную смещения x по времени. Согласно уравнению колебаний частиц в волне смещение x = Acos( 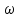 t + α0 ) . t + α0 ) .Скорость частиц изменяется с течением времени по закону 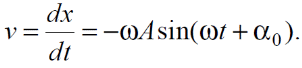  Пример 3. Во сколько раз различаются интенсивности волн, если разность уровней интенсивности 1 дБ? {Ответ: в 1,26 раза} Пример 4. Вентилятор создает звук, уровень интенсивности которого L = 60 дБ. Найти уровень интенсивности звука при работе двух рядом стоящих вентиляторов. { Ответ: 63 дБ} Пример 5. Отношение интенсивностей двух источников звука I1/ I 2 = 2. Чему равна разность уровней интенсивностей этих звуков? { Ответ: 3 дБ} Пример 6. Каков уровень интенсивности звука с частотой 100 Гц, который имеет ту же громкость, что и звук с частотой 3 кГц и интенсивностью 25 дБ? { Ответ: 65 дБ} Пример 7. Амплитуда звуковой волны увеличилась в три раза. а) Во сколь- ко раз возросла ее интенсивность? б) На сколько децибел увеличился уро- вень громкости? { Ответ: а) в 9 раз; б) на 9,5 дБ} Домашнее задание: Человеческое ухо воспринимает упругие волны в интервале час- тот от 1 = 16 Гц до 2 = 20 кГц. Каким длинам волн соответствует этот ин- тервал в воздухе и в воде? Скорость звука в воздухе и воде соответственно = 340 м/с и 2 = 1400 м/с. {в воздухе: 117 м , 2 0,017 м; в воде: 170 м, 20,07 м}. Определите среднюю силу, действующую на барабанную перепонку уха человека (площадь s 66 мм2 ), для двух случаев: а) порог слышимости; б) порог болевого ощущения. Частота равна 1 кГц. {а) 1,95 нН; б) 6,17 мН}. Нормальный разговор человека оценивается уровнем громкости звука Е1 = 50 фон. Определите уровень громкости звука, соответствующе- го трем одновременно говорящим людям. Частоту звука условно считать = 1 кГц. {54,8 фон} Уровень громкости звука реактивного самолета на расстоянии 30 м от него равен 140 дБ. Каков уровень громкости на расстоянии 300 м? Отражением от земли пренебречь. {120 дБ} Звук, которому на улице соответствует уровень интенсивности L 150 дБ, слышен в комнате так, как звук с уровнем интенсивности L 230 дБ. Найдите отношение интенсивностей этого звука на улице и в комнате. {L 1 / L 2 100} Уровень громкости звука с частотой 5000 Гц равен Е 50 фон. Найдите интенсивность этого звука, воспользовавшись кривыми равной громкости. { 5 108Вт/м 2} Тема 12. Основные характеристики электрического поля: напряженность и потенциал. Напряженность электрического поля диполя. Электрический момент диполя. Теорема Гаусса-Остроградского, ее применение для расчета электрических полей. Проводники в электрическом поле. Электроемкость. Энергия заряженного конденсатора. Объемная плотность энергии электрического поля в вакууме и в диэлектриках. Поляризация диэлектриков. Электрическая проницаемость вещества. Диэлектрическая проницаемость биологических объектов. Пример.1 Для изучения структуры и функции биологических мембран используют модели – искусственные фосфолипидные мембраны, состояние из бимолекулярного слоя фосфолипидов. Толщина искусственной мембраны достигает около l=6 нм. Найдите электроёмкость 1 см2 такой мембраны, считая её относительную диэлектрическую проницаемость εr=3. Сравните полученную электроёмкость с аналогичной характеристикой конденсатора, расстояние между пластинами которого l=1 мм.  Пример.2 Какой максимальный момент силы действует в электрическом поле с напряжённостью E=20 кВ/м на молекулу воды (p=3.7*10-29 Кл*м)? В чём отличие действия на молекулу однородного и неоднородного полей? 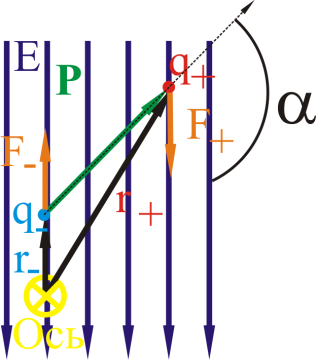    Домашнее задание:    Тема 13. Электрический ток. Элементы электронной теории проводимости твердых тел Пьезоэлектрический эффект. Постоянный электрический ток. Плотность тока. Закон Ома в дифференциальной. форме. Сопротивление проводников. Сверхпроводимость. Элементы электронной теории проводимости твердых тел. Понятие о зонной теории твердых тел. Контактная разность потенциалов. Термоэлектродвижущая сила. Термопары. Термостолбики. Явление Пельтье, его применение в холодильниках. Применение термохолодильников в фармации и медицине. Пример 1. Термопарой можно определить минимальное Изменение температуры в 0,006∘С. Определить сопротивление гальванометра чувствительностью 1,5⋅10−8 А, если сопротивление термопары 6Ом и коэффициент пропорциональности термопары равен 0,05 мВ/град. Э. д. с. термопары E=αΔt. Эта э. д. с. должна создать ток в цепи гальванометра, который не должен быть меньше чувствительности гальванометра i. По закону Ома для полной цепи I=E/(Rg+r)=αΔt/(Rg+r), где Rg - сопротивление гальванометра, r - сопротивление термопары, α — коэффициент пропорциональности термопары, Δt - минимальное изменение температуры. Из полученного уравнения определяем сопротивление гальванометра: Rg=(αΔt−ir)/i; Rg=14Ом Пример 2. Какова температура печи, если помещенная в нее термопара железо — константан (k=0,05мВ/град) дает па гальванометре чувствительностью 10−7 A/дел и сопротивлением 1000 Ом отклонение на 200 делений? Второй спай термопары погружен в тающий лед.  Пример 3. В цепь гальванометра включена термопара, состоящая из медной и константановой проволочек длиной по 1 м и диаметра 0,2 мм. Чувствительность гальванометра 10−6 А/дел; его внутреннее сопротивление равно 50 Ом. На сколько делений отклонится стрелка гальванометра, если спай термопары перегреть на 50∘С по отношению к температуре окружающей среды? Э. д. с. термопары 40 мкВ/град, удельное сопротивление константана 0,50⋅10−4 ом⋅см и меди 0,17⋅10−5 Ом⋅см.  Пример 4. Термопара εТ железо—константан и соединенный с нею последовательно гальванометр включены, как показано на рисунке, где ε - батарея с ЭДС, равной 1,5 В. Полное сопротивление потенциометра равно 15 кОм. Холодный спай термопары находится в сосуде с тающим льдом. Постоянная термопары α=5,3⋅10−5 В/К. Определите температуру горячего спая термопары, если при сопротивлении RAB=150Ом сила тока в цепи гальванометра равна нулю. Внутренним сопротивлением батареи пренебречь. 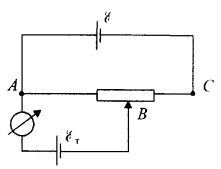 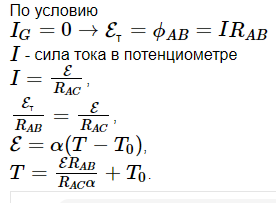 Ответ: Т=283 ͦ С Домашнее задание: Определить чувствительность гальванометра, если при включении его в цепь термопары с коэффициентом пропорциональности 0,05 мВ/град отклонение стрелки достигает 100 делений при разности температур 400∘С. Сопротивление гальванометра 10000 Ом. Разность температур между спаями термопары составляет 800 С, это приводит к появления термо - ЭДС величиной в 0,8 В. Каков коэффициент чувствительности такой термопары? Сила тока в цепи, состоящей из термопары с сопротивлением R1 = 4 Ом и гальванометра с сопротивлением R2 = 80 Ом, / = 26 мкА при разности температур спаев ΔT = 50°С. Чему равна постоянная термопары? Для определения температуры нагревательной установки в нее вставлена термопара «никель-нихром» с постоянной χ = 0,5·10-6 В/К, присоединенная к гальванометру с внутренним сопротивлением R = 2000 Ом и с чувствительностью 10-8 А /дел. При температуре второго спая Т2 = + 15°С гальванометр показывает отклонение n = 25 делений. Чему равна температура установки? |
