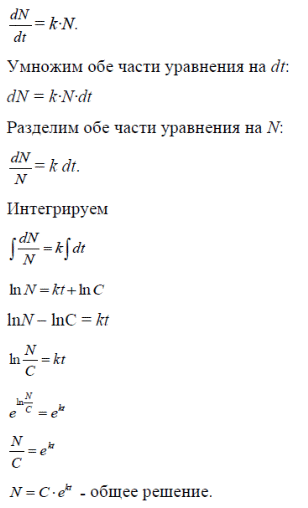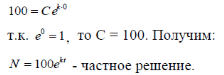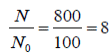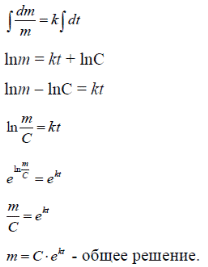Задачи по программе фарм. Тема 1 Измерение физических величин. Прямые и косвенные измерения. Ошибки и погрешности измерений физических величин. Прямые и косвенные измерения. Обработка результатов прямых измерений. Прямые измерения

• Название: Тема 1 Измерение физических величин. Прямые и косвенные измерения. Ошибки и погрешности измерений физических величин. Прямые и косвенные измерения. Обработка результатов прямых измерений. Прямые измерения
• Дата: 06.03.2023
• Размер: 5.58 Mb.
• Имя файла: Задачи по программе фарм.docx
• Тип: Решение; #972214
• страница: 2 из 4

Тема 5. Основные понятия и приемы интегрирования. Неопределенный интеграл. Определенный интеграл.

Пример 1. Найти неопределенный интеграл.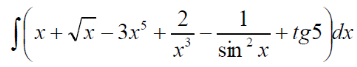



Решение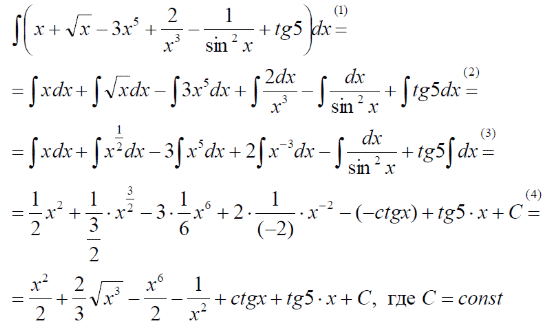





Пример 2. Найти неопределенный интеграл.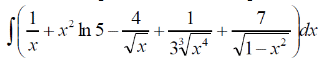



Решение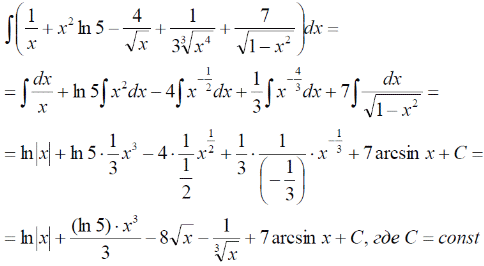





Пример 3. Найти неопределенный интеграл.



Преобразуем подынтегральную функцию в сумму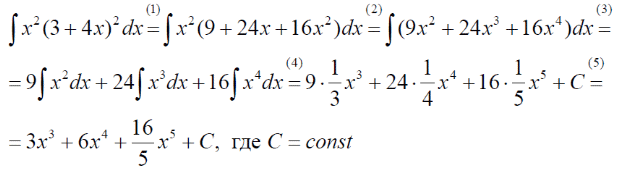



Подведение функции под знак дифференциала

Пример 3. Найти неопределенный интеграл



Подведём функцию (3x +1) под знак дифференциала: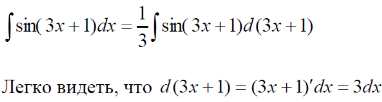





Пример 4. Найти неопределенный интеграл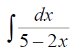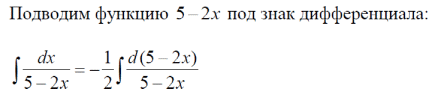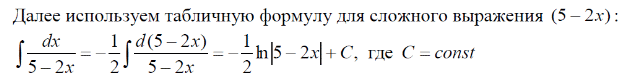







Примеры 5-7 :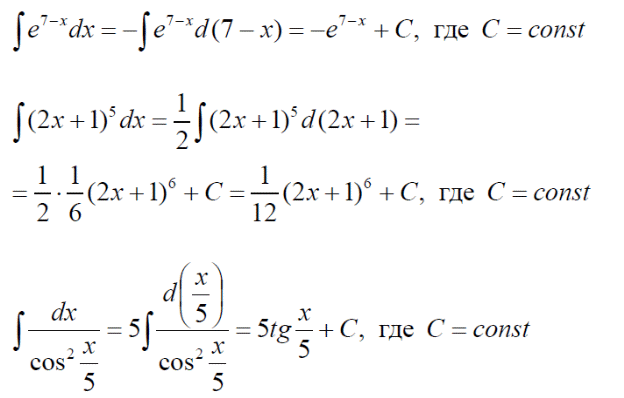



Метод замены переменной в неопределённом интеграле

Пример 4. Найти неопределенный интеграл



Метод замены переменной состоит в том, чтобы сложное выражение заменить одной буквой. В данном случае напрашивается замена 3x +1= t . Также dx нужно превратить в некоторое выражение, которое зависит только от t. Записываем дифференциал:

,

.

и переход к новой переменной осуществлён: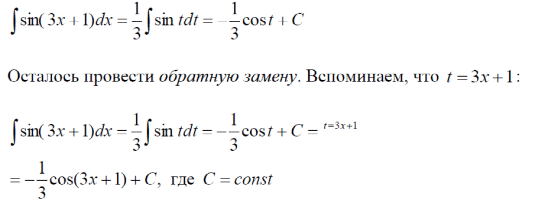


Пример 4. Найти неопределенный интеграл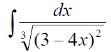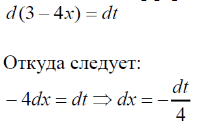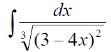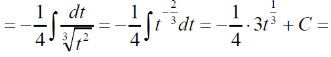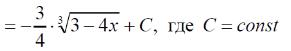










Пример 4. Найти неопределенный интеграл



Решение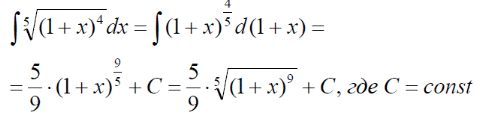


Пример 4. Найти неопределенный интеграл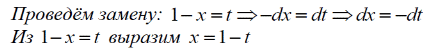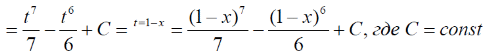









Пример 4. Найти неопределенный интеграл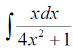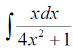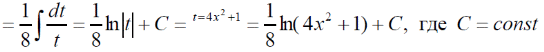






Пример из физики


Домашнее задание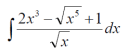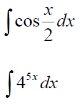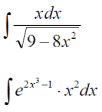

, , ,

,

Определённые интегралы

Пример 1. Вычислить определенный интеграл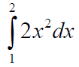



Решение: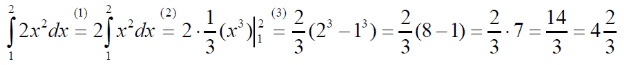



Пример 2. Вычислить определенный интеграл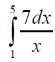



Решение: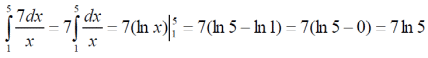



Пример 3. Вычислить определенный интеграл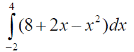



Решение: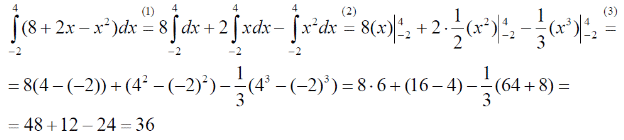



Домашнее задание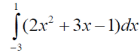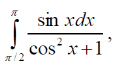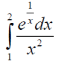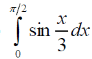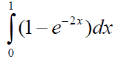

, , ,

Тема 6. Понятие об обыкновенных дифференциальных уравнениях (ДУ). Порядок дифференциальных уравнений. Уравнение движения материальной точки-пример линейного ДУ. Второй закон Ньютона -пример ДУ второго порядка. Задачи, приводящие к ДУ.

Пример 1. Найти общее решение дифференциального уравнения

у3х²1

Решение:

Уравнение представлено через производную, поэтому еѐ надо заменить

на отношение дифференциалов dy/dx;



Разность двух постоянных С2 – С1 есть величина постоянная, поэтому

можно еѐ заменить на постоянную интегрирования С.

y x³x C - общее решение уравнения.
Пример 2. Найти общее решение дифференциального уравнения





Интегрируем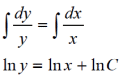



Здесь произвольная постоянная взята в логарифмической форме.



- общее решение дифференциального уравнения.
Пример 3. Найти общее решение дифференциального уравнения





Интегрируем





Потенцируем это выражение и выражаем функцию y.

- общее решение дифференциального уравнения.

Пример 4. Найти частное решение дифференциального уравнения


Вначале найдем общее решение дифференциального уравнения.

В левой части уравнения должен стоять y, поэтому разделим обе части

уравнения на 6: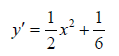



Заменим производную отношением дифференциалов: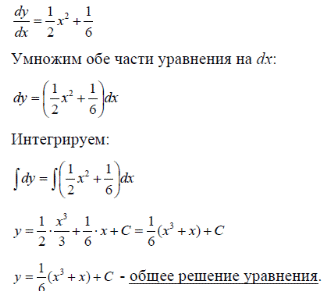



Чтобы найти частное решение, необходимо использовать начальные

условия, подставим х = 1 и у = 6 в общее решение и найдем значение постоянной интегрирования С: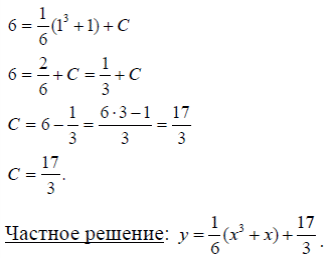



Пример 5. Найти частное решение дифференциального уравнения


Решение:

Вначале найдем общее решение данного дифференциального уравнения. В левой части уравнения оставим y, все остальное перенесѐм в правую

часть:

y= у + 6

Заменим производную отношением дифференциалов: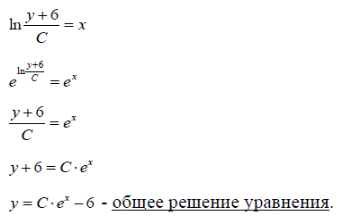




Подставим х = 0 и у = 5 в общее решение и найдем значение постоян-

ной интегрирования С: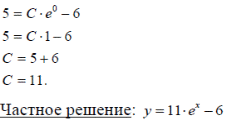



Пример 6. Найти частное решение дифференциального уравнения



Решение:

Вначале найдем общее решение дифференциального уравнения.

В данном уравнении производная уже заменена отношением дифференциалов и обе части уравнения умножены на dx.

В левой части уравнения должен стоять dy, поэтому обе части уравне-

ния делим на 2: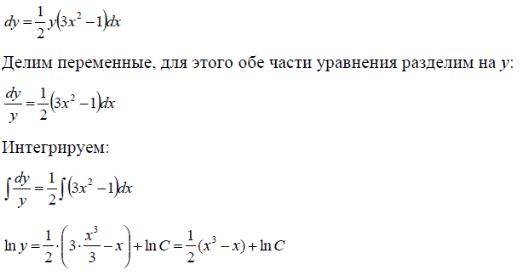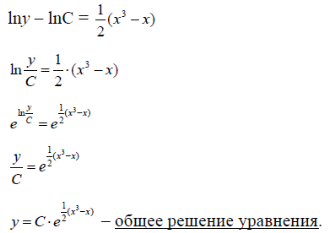





Подставим х = 1 и у = 3 в общее решение и найдем значение постоян-

ной интегрирования С: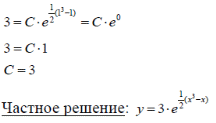



Пример 7. Скорость размножения бактерий пропорциональна их количеству. В начальный момент имелось 100 бактерий. В течение 3 часов их число удвоилось. Найти зависимость количества бактерий от времени. Во сколько раз увеличится количество бактерий в течение 9 часов?
Решение:

Пусть N – количество бактерий в момент t. Согласно условию задачи скорость размножения бактерий пропорциональна их количеству, т. е.

N N или N= k∙N,

где k - коэффициент пропорциональности.
Получили дифференциальное уравнение первого порядка с разделяю-

щимися переменными. Решим его. Заменяем производную отношением дифференциалов:



Используя первую пару начальных условий, определим постоянную

интегрирования C: t0 = 0, N0 = 100.



Используя вторую пару начальных условий, определим коэффициент

пропорциональности k: t1 = 3, N1 = 200.



Разделим обе части уравнения на 100.





Следовательно, зависимость количества бактерий от времени имеет вид:



Вычислим количество микроорганизмов через t2 = 9 часов.





Вывод: в течение 9 часов количество бактерий увеличилось в 8 раз.
Пример 8. Какая часть введенного лекарства в организме распадется через 4 часа, если через 2 часа после введения 4 мг препарата его масса уменьшилась

вдвое?

Решение:

Пусть m – количество лекарственного препарата в организме в момент t. Согласно условию задачи скорость распада пропорциональна начальному количеству лекарственного препарата в организме, т. е.

m m или m= k∙m,

где k - коэффициент пропорциональности.

Получили дифференциальное уравнение первого порядка с разделяю-

щимися переменными. Заменяем производную отношением дифференциалов:







Следовательно, зависимость количества лекарства от времени имеет вид:



Теперь узнаем количество вещества в организме через 4 часа (t=4).



Через 4 часа в организме находится 1 мг препарата. За это время распалось



Ответ: За 4 часа в организме распалось ¾ части лекарственного препарата (75%).

Пример. Груз массой 320 г подвешен на легкой пружине и выведен из состояния покоя вытягиванием пружины на 8 см, при этом возникла сила упругости 1 Н. Затем груз подбросили вертикально вверх, придав ему начальную скорость 0,5 м/с. Найти период и амплитуду свободных колебаний груза, если движение происходит без сопротивления.
Решение.

Обозначим через s(t) отклонение груза от положения равновесия. Колебания вызываются силой упругости

F = kх,

причем так как при удлинении пружины на 8 см сила упругости составила 1 Н, то коэффициент жесткости

k =1/0,08= 12,5 кг/c² .

Запишем второй закон Ньютона

ma = −kх,

откуда получим линейное однородное уравнение второго порядка

0,32 х ′′+12,5х=0

. Характеристическое уравнение

0,32 λ² +12,5 =0

имеет корни ,

λ_1,2 =±6,25i

значит, общее решение записывается в виде .
х = С₁ cos 6, 25 t +С₂ sin 6, 25t

Домашнее задание

1.