Зачетное задание по школьной математике. Зачетное задание по алгебре. Решение разделим обе части уравнения на. Промежутку принадлежат два корня и
 Скачать 1.24 Mb. Скачать 1.24 Mb.
|
Зачетное задание по алгебреВариант 1.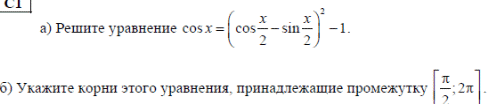 Решение: 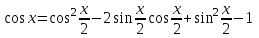 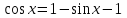 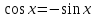 разделим обе части уравнения на разделим обе части уравнения на 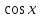 . .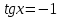 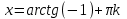 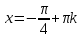 Промежутку 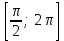 принадлежат два корня принадлежат два корня 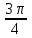 и и 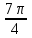 . .Решите систему уравнений 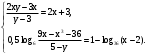 Решение: ОДЗ: 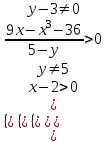 , , 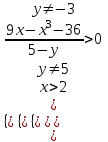 Рассмотрим первое уравнение системы 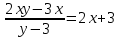 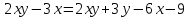 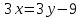 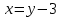 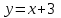 - подставим во второе уравнение системы - подставим во второе уравнение системы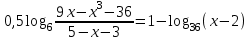 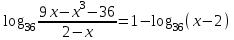 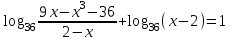 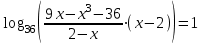 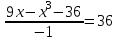 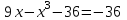 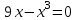 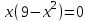  ; ; 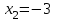 ; ; 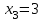 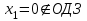 ; ; 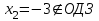 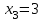 , тогда , тогда 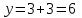 Сделаем проверку 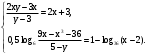 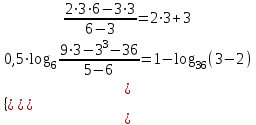 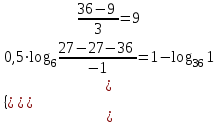  Ответ: (3; 6) Найдите все значения х, для которых точки графика функции 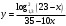 лежат ниже соответствующих точек графика функции лежат ниже соответствующих точек графика функции 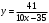 . . Решение Нам нужно решить неравенство 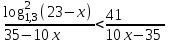 Будем решать неравенство методом интервалов ОДЗ: 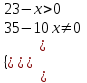 ; ; 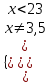 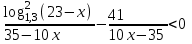 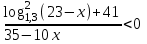 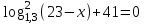 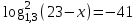 нет решений нет решений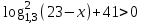 для всех для всех 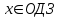 . .То есть рассмотрим выполнение неравенства на двух интервалах 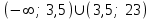 . .При 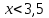 неравенство не выполняется; неравенство не выполняется;При 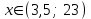 неравенство выполняется. неравенство выполняется.Ответ: точки графика функции 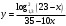 лежат ниже соответствующих точек графика функции лежат ниже соответствующих точек графика функции 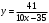 при при 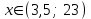 . .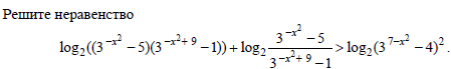 Решение: ОДЗ: 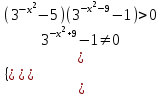 Рассмотрим первое неравенство 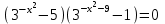 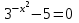 или или 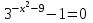 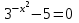 , , 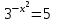 , , 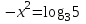 нет решений; нет решений;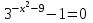 , , 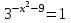 , , 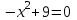 , , 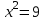 , , 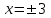 . .Первое неравенство выполняется при 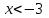 и и 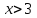 . .ОДЗ: 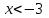 и и 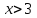 . .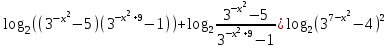 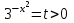 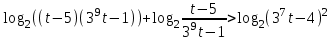 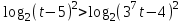 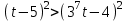 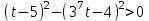 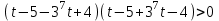 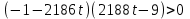 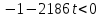 для всех для всех 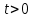 , следовательно, неравенство выполняется при , следовательно, неравенство выполняется при 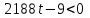 , , 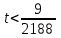 . .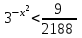 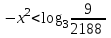 , , 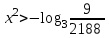 , , 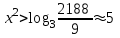 , , 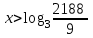 , , 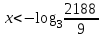 Ответ: с учетом ОДЗ 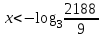 , , 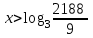 Зачетное задание по стереометрииВариант 1В единичном кубе A...D1 найдите угол между прямыми АВ1 и ВС1. Решение 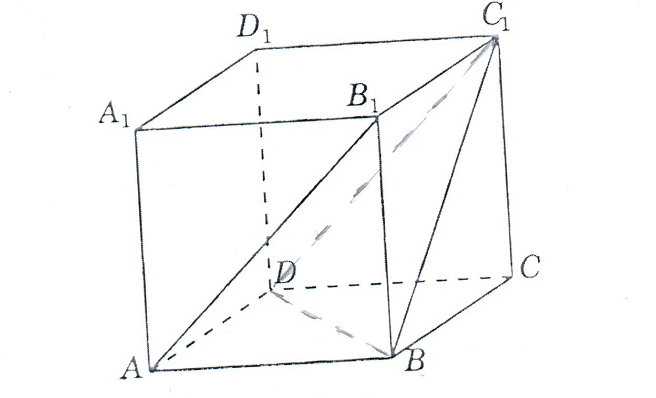 Углом между скрещивающимися прямыми АВ1 и ВС1 будет угол между прямой 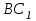 и прямой и прямой 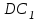 , параллельной прямой , параллельной прямой 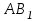 . .Рассмотрим треугольник 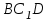 . Все стороны этого треугольника диагонали квадратов со стороной 1. То есть все стороны равны между собой. Значит . Все стороны этого треугольника диагонали квадратов со стороной 1. То есть все стороны равны между собой. Значит 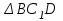 равносторонний. В равностороннем треугольнике все углы равны равносторонний. В равностороннем треугольнике все углы равны 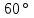 . Угол . Угол 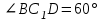 . Следовательно, угол между прямыми АВ1 и ВС1 равен . Следовательно, угол между прямыми АВ1 и ВС1 равен 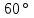 . .Ответ: 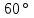 . .2.1. В правильной шестиугольной призме 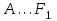 , все ребра которой равны 1, найдите угол между прямой , все ребра которой равны 1, найдите угол между прямой 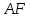 и плоскостью и плоскостью 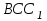 . .Решение 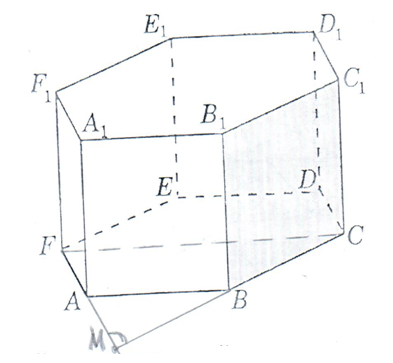 Угол между прямой и плоскостью это угол между прямой и ее проекцией на эту плоскость. Проекцией прямой 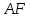 на плоскость на плоскость 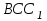 будет прямая будет прямая 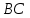 . То есть, нам надо найти величину угла АМВ. . То есть, нам надо найти величину угла АМВ.Рассмотрим 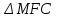 . .  . . 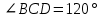 , как угол правильного шестиугольника. , как угол правильного шестиугольника.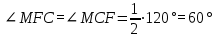 . .То есть 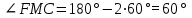 . То есть, искомый угол равен . То есть, искомый угол равен 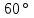 . .Ответ: 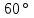 . .3.1. В правильной шестиугольной призме 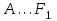 , все ребра которой равны 1, найдите угол между плоскостями , все ребра которой равны 1, найдите угол между плоскостями 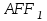 и и 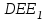 Решение 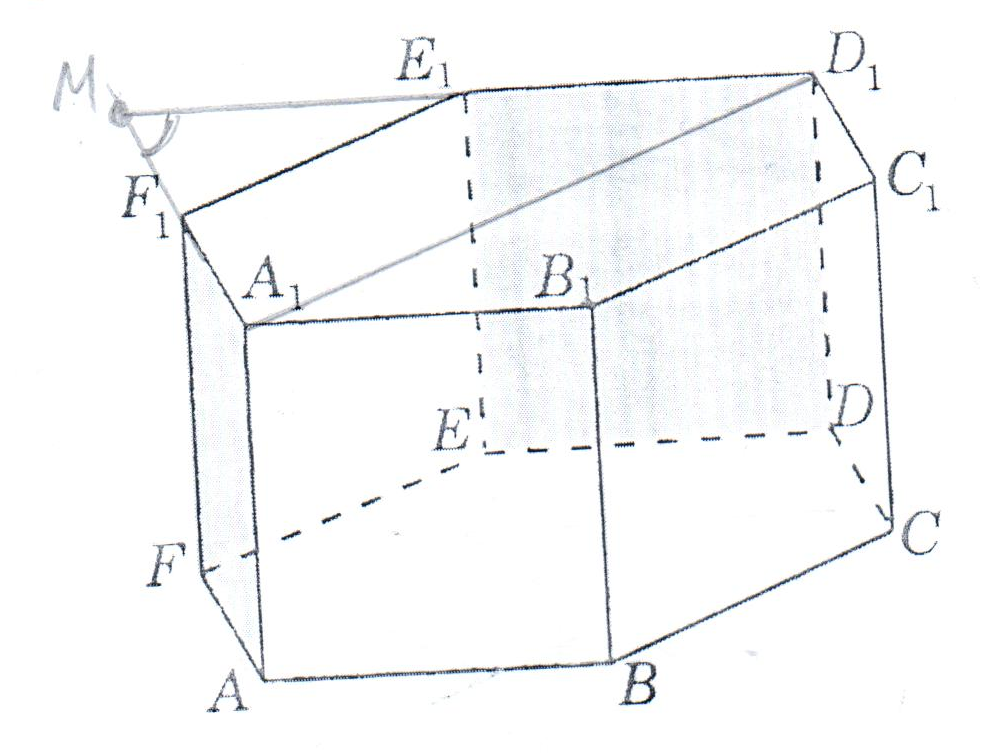 Угол между плоскостями это угол между прямыми, образованными при пересечении заданных плоскостей, плоскостью, перпендикулярной линии пересечения данных плоскостей. Так как основание прямой призмы перпендикулярно боковым ребрам призмы, то плоскость 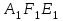 перпендикулярна плоскостям перпендикулярна плоскостям 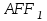 и и 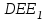 . То есть, нам нужно найти величину угла М. . То есть, нам нужно найти величину угла М.В треугольнике 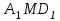 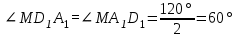 , следовательно, , следовательно, 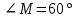 . .Ответ: 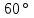 . .В правильной шестиугольной призме 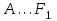 все ребра которой равны 1, найдите расстояние от точки все ребра которой равны 1, найдите расстояние от точки 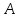 до прямой до прямой 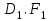 . .Решение 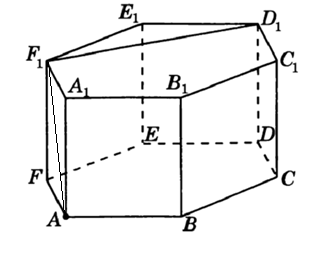 Расстояние от точки до прямой - это длина перпендикуляра, проведенного из точки к прямой. 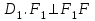 , т. к. в правильной призме боковые грани (и ребра) перпендикулярны основаниям. , т. к. в правильной призме боковые грани (и ребра) перпендикулярны основаниям.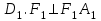 , т. к. , т. к. 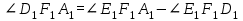 , , 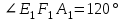 (внутренний угол правильного шестиугольника), (внутренний угол правильного шестиугольника), 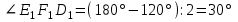 (угол при основании равнобедренного (угол при основании равнобедренного  ). ).Значит, прямая  перпендикулярна плоскости перпендикулярна плоскости 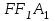 , а значит, любая прямая, лежащая в этой плоскости перпендикулярна , а значит, любая прямая, лежащая в этой плоскости перпендикулярна 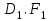 . Значит, . Значит, 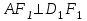 . То есть, расстоянием от точки . То есть, расстоянием от точки 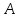 до прямой до прямой 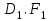 будет длина отрезка будет длина отрезка 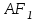 . . 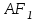 - диагональ квадрата со стороной 1. По теореме Пифагора - диагональ квадрата со стороной 1. По теореме Пифагора 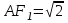 . .Ответ: расстояние от точки 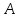 до прямой до прямой 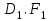 равно равно 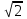 . .5.1. В единичном кубе 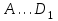 найдите расстояние от точки найдите расстояние от точки 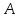 до плоскости до плоскости 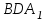 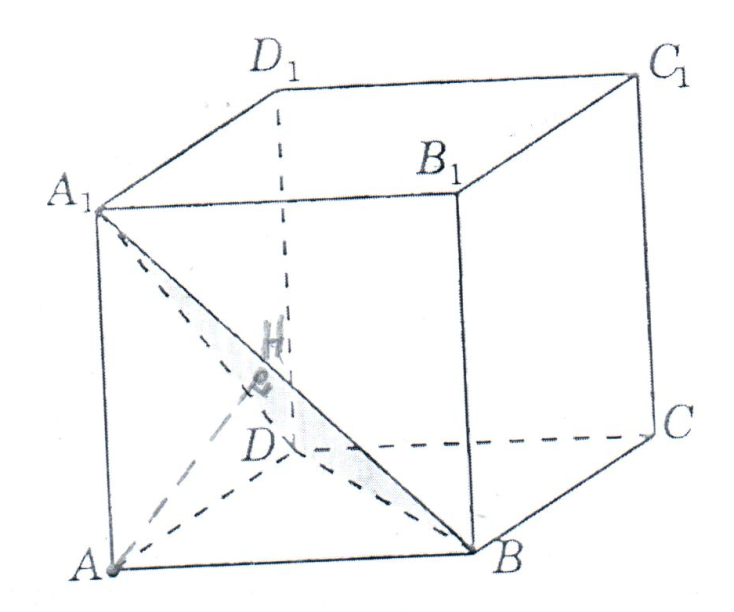 Решение Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на плоскость. 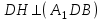 , длина отрезка , длина отрезка 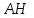 - расстояние от точки - расстояние от точки 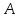 до плоскости до плоскости 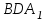 . .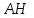 - высота пирамиды - высота пирамиды 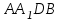 . Объем пирамиды . Объем пирамиды 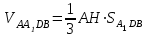 . .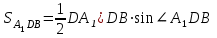 . . 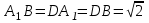 (диагонали единичных квадратов), (диагонали единичных квадратов), 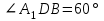 . .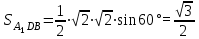 . .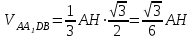 . .С другой стороны, 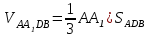 . . 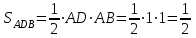 . .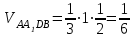 . .Приравниваем объемы пирамиды 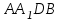 : : 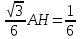 , откуда , откуда  . .Ответ: расстояние от точки 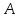 до плоскости до плоскости 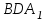 равно равно 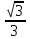 . .6.1. В правильной четырехугольной пирамиде 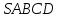 , все ребра которой равны 1, найдите расстояние между прямыми , все ребра которой равны 1, найдите расстояние между прямыми 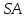 и и 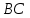 . .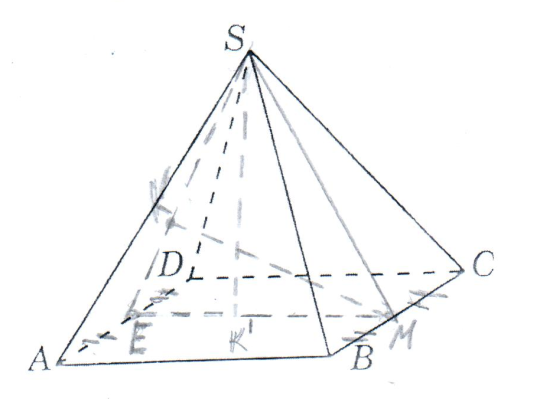 Решение Расстояние между скрещивающими прямыми равно расстоянию от любой точки этой прямой до плоскости, проходящей через вторую прямую, параллельно первой прямой. Плоскость 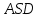 параллельна прямой параллельна прямой 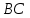 , так как , так как 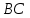 параллельна прямой параллельна прямой 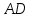 , лежащей в плоскости , лежащей в плоскости 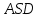 . То есть, расстояние между прямыми . То есть, расстояние между прямыми 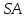 и и 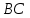 это расстояние от любой точки это расстояние от любой точки 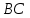 до плоскости до плоскости 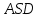 . .Построим плоскость 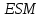 . . 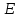 - середина - середина 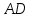 , , 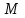 - середина - середина 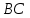 . . Так как треугольники 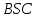 и и 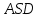 правильные, то их медианы являются высотами. Плоскость правильные, то их медианы являются высотами. Плоскость 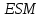 будет перпендикулярна прямой будет перпендикулярна прямой 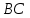 и плоскости и плоскости 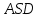 . .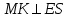 , , 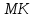 - расстояние между прямыми - расстояние между прямыми 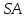 и и 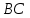 . .Рассмотрим 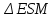 . Его площадь можно найти двумя способами. . Его площадь можно найти двумя способами.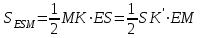 , то есть , то есть 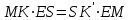 . .В прямоугольном треугольнике 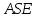 : : 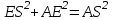 , , 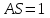 (по условию), (по условию), 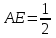 (по построению). (по построению).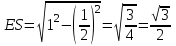 . .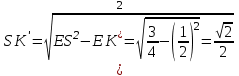 . . 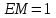 . .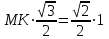 , , 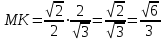 . .Ответ: расстояние между прямыми 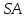 и и 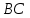 равно равно 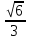 . . |
