матем атика. математика. Задача Вычислить определённый интеграл Сначала нужно найти неопределенный интеграл
 Скачать 32.18 Kb. Скачать 32.18 Kb.
|
|
Задача 1. Воспользовавшись таблицей интегралов и основными методами интегрирования, найти следующие интегралы: 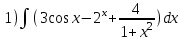 По свойству интегралов: 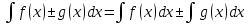 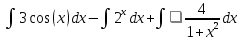 Используя свойства: 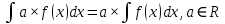 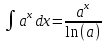 3sin(x)- 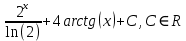 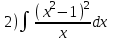 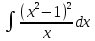 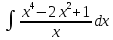 Разделим дробь 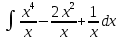 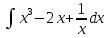 Используя свойство 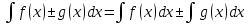 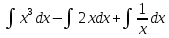 Используя 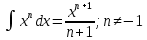 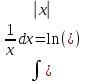 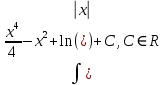 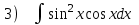 Используя метод подстановки Пусть sin(x)=t 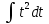 Используя 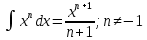 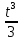 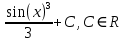 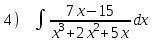 Разложим знаменатель. 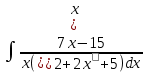 Используя метод неопределенных коэффициентов. 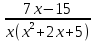 = = 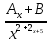 + +  = =  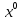 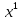 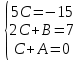 = =  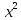 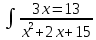 - - 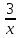 dx = dx = 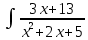 dx - 3 dx - 3 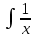 dx = dx == -3 In ( 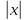 ) + ) + 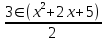 + 5arctg ( + 5arctg (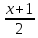 ) )Задача 2. Вычислить определённый интеграл:  Сначала нужно найти неопределенный интеграл Используя Dx=  xdt, где t=ln(x) и t’= xdt, где t=ln(x) и t’= Подставим ln(x)=t 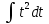 Используя 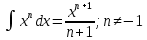   Используя 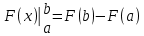 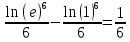 Пояснение 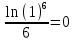 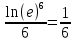 Задача 3. Вычислить площадь фигуры, ограниченной линиями: 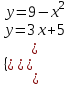 - 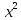 -3x + 4 = 0 -3x + 4 = 0D = 9+16 = 25 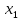 = -4; = -4; 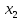 = 1 = 19 - 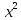 = 3x + 5 = 3x + 5- 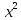 -3x + 4 = 0 -3x + 4 = 0 -3x+4)dx -3x+4)dxНайдем неопределенный интеграл. По свойству 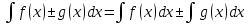 - 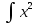 dx - dx -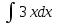 + +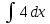 По свойству 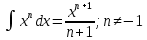 - 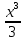 - -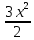 +4 +4(- 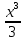 - - 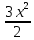 +4x) +4x)По свойству 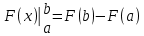 - 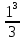 - - 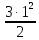 +4-(- +4-(-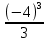 - -  +4 +4 (-4)) = (-4)) =  = 20 = 20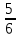 = 20,83 = 20,83Задача 4. Исследовать на сходимость ряд с положительными членами: 3) 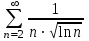 F(x)= 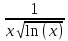 Так как функция положительная, непрерывная, убывает при x 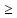 2, то можно использовать интеграл 2, то можно использовать интеграл  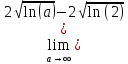 Предел + 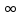 , значит несобственный интеграл расходится , значит несобственный интеграл расходитсяЗадача 5. Определить тип дифференциального уравнения первого порядка и найти его общее решение: 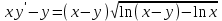 Переместим в левую часть x 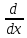 y(x)-(x-y(x)) y(x)-(x-y(x))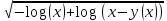 -y(x)=0 -y(x)=0замена Пусть u(x)= 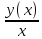 y(x)=xu(x)  Поставим 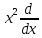 u(x)+x u(x)+x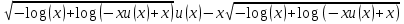 =0 =0Дифференцированное уравнение вида F1(x)g1(u)u’=f2(x)g2(u) 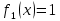 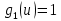 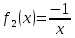 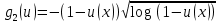 Разделим на 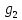 -(1-u(x))  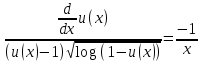 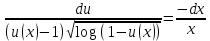 Интегралы слева по u, спарава по x  2 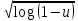 =Const-log(x) =Const-log(x)U(x)=1- 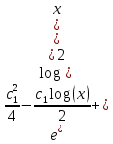 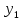 =y(x)=x(1- =y(x)=x(1-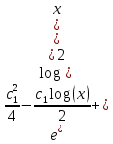 ) ) |
