МАТЕМАТИКА. +РР2 Математика (Шамраева) (1). Кафедра Математика и информатика
 Скачать 154.29 Kb. Скачать 154.29 Kb.
|
 Кафедра ___Математика и информатика_________________________ Рейтинговая работа _______________________________________________ (домашняя творческая работа, расчетно-аналитическое задание, реферат, контрольная работа) по дисциплине _________________________________________________ Задание/вариант № ______6______ Тема* ______________________________________________________________ Выполнена обучающимся группы _ Стражинская Любовь Ивановна __ __________________________________________________________________ (фамилия, имя, отчество) Преподаватель ____________________________________________________ (фамилия, имя, отчество) Москва – 201__ г. * при наличии ВАРИАНТ 6 Задача 1. Воспользовавшись таблицей интегралов и основными методами интегрирования, найти следующие интегралы:  Решаем почленно: 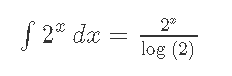 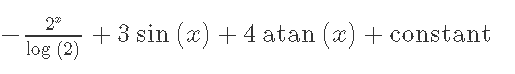 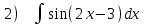 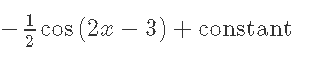 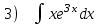 Используем интегрирование по частям То есть после замены получается: Теперь решаем вторую часть подинтеграл: Результат вычислений: 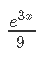 Соединив 2 части получаем:  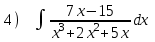 Перепишем подынтегральное выражение: 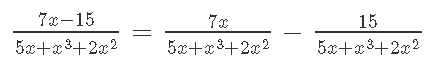 Найдём интеграл от 1 члена: 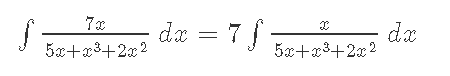 Сокращаем в подынтегральном выражении x: 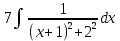 Использую таблицу интегралов получаем: 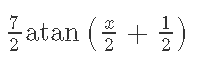 Переходим ко второму члену интеграла: 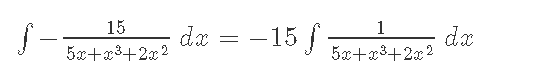 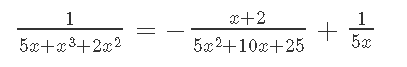 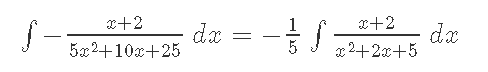 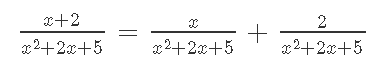 Интегрируем почленно:  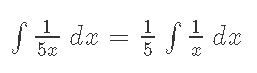 То есть: 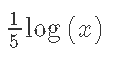 Ответ: Задача 2. Вычислить определённый интеграл: 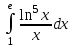 Натуральный логарифм из e равне 1, при возведении получается так же 1, при умножении на 1/6 получается 1/6. Натуральный логарифм из 1 равне 0. Соответственно вычитать мы будем 0. Ответ 1/6 Задача 3. Вычислить площадь фигуры, ограниченной линиями: 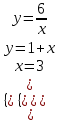 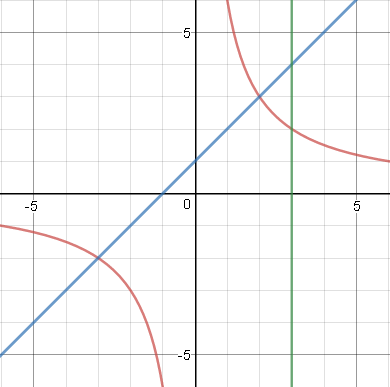 Необходимо вычислить: 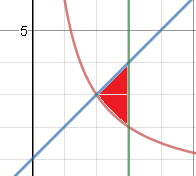 Для этого из это площади: 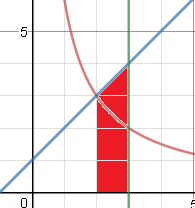 Необходимо удалить эту: 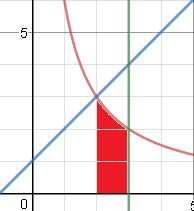 Необходимо вычислить точки пересечения линий: 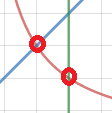 1+x= 6/x X=2 Вторая точка X=3 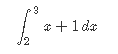 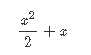 Первая площадь равна 3,5 Определяем следующую площадь фигуры 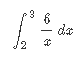 Площадь равна 2,43 Искомая площадь равна 3,5-2,43=1,07 Задача 4. Исследовать на сходимость ряд с положительными членами: 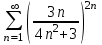 Это ряд вида: Степенной ряд. 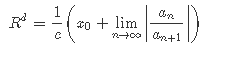 В нашем случае: 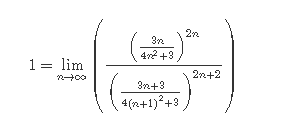 Функция стремится к бесконечности. Задача 5. Определить тип дифференциального уравнения первого порядка и найти его общее решение: 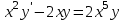 Имеем линейно уравнение Разделим обе части Получим: 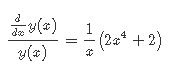 Далее домножим обе части на dx/  Берем интегралы 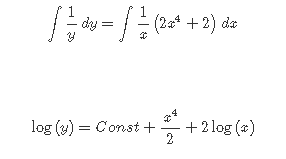 Мы получили обыкновенное уравнение с неизвестной y |
