Практическая работа 1 Определение инструментальной погрешности и ошибки центрирования сигнала и теодолита по результатам специальных исследований
 Скачать 22.18 Kb. Скачать 22.18 Kb.
|
|
Практическая работа №1 «Определение инструментальной погрешности и ошибки центрирования сигнала и теодолита по результатам специальных исследований» Цель задания: научиться определять фактические погрешности измерения угла и ошибки центрирования теодолита и сигналов. Исходные данные: угол с одинаковыми длинами сторон a=b=50м. Ход решения: Находим среднее квадратические ошибки из каждой серии измерений: Первая серия измерений: В первой серии исследований производится многократное измерение угла без смещения теодолита и сигналов (т.е. берём отсчёты без центрирования теодолита и сигнала)
σ= 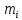 = =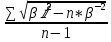 = =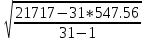 = = =12,573 =12,573Вторая серия измерений: Во второй серии наблюдений перед каждым измерением угла заново центрировался один из сигналов. Ошибка второй серии- ошибка инструмента+ ошибка центрирования.
σⅡ= 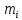 = =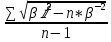 = =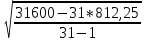 = =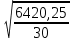 =14,629 =14,629Третья серия измерений: В третьей серии наблюдений каждый раз изменялась центрировка теодолита. Среднее квадратическое отклонение, найденное в третьей серии измерений, включает в себя инструментальную ошибку и ошибку от неправильного центрирования теодолита.
σⅢ= 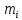 = =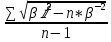 = =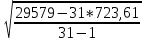 = = = 15,434 = 15,434Так как σ меньше σⅡ, а σⅡ меньше σⅢ, порядок серий остаётся неизменным. σ = 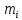 = 12,573; = 12,573;σⅡ =14,629; σⅢ =15,434. Находим среднюю ошибку измерения угла из-за неточности центрирования сигнала: σⅡ = 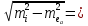  = = 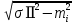 = = 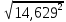 - - 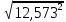 = 7, 48 , = 7, 48 ,Где 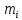 - инструментальная ошибка измерения угла. - инструментальная ошибка измерения угла.Из формулы  = = 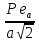 нахожу нахожу 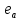 : :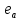 = = 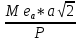 = = 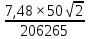 = 2,6 * = 2,6 * 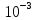 м. м.Находим среднюю ошибку измерения угла из-за неточности центрирования теодолита: σⅢ = 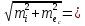  = = 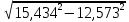 = 8,95 = 8,95Из формулы 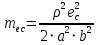 ( (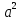 + +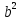 - 2 * a * b * cosβ) с учётом того, что a=b=50м, нахожу - 2 * a * b * cosβ) с учётом того, что a=b=50м, нахожу  : : = =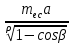 = = 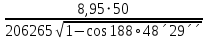 = =  = 1,5 * = 1,5 * 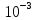 м. м.Вывод: в ходе данной работы я научилась определять инструментальную погрешность теодолита, линейные ошибки сигнала и погрешность от неправильного центрирования инструмента. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 =547,56
=547,56