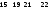Основы управления. Практическая работа 1 Планирование движения спецподразделений по объектам

• Название: Практическая работа 1 Планирование движения спецподразделений по объектам
• Анкор: Основы управления
• Дата: 23.09.2021
• Размер: 0.62 Mb.
• Имя файла: Osnovy_upravlenija_stroitelstvom.doc
• Тип: Практическая работа; #235717
• страница: 2 из 6

Методические указания по выполнению


В матричной форме расчет ведется в следующем порядке (табл.1.2):

1. Начало каждого процесса (ni) на каждом объекте (Nj) (захватке) равно окончанию этого процесса на предыдущем объекте (захватке) и записывается в верхнем левом углу:

Таблица 1.2

Ключ матрицы

N	i	i + 1
j	tн (ij) tо (ij) t (ij)	tн (i + 1) ,j tо(i + 1) ,j t (i + 1),j
j + 1	tн i, (j + 1) tо i, (j + 1) tорг t i, (j + 1)	tн (i +1; j + 1) tо (i+1; j + 1) t (i+1; j+1)

Условные обозначения:

• 
  i – номер процесса (спецподразделения);
  
• 
  j – номер объекта (захватки);
  
• 
  t(ij) – продолжительность i-го процесса на j-м объекте (захватке);
  
• 
  t_н (ij) – начало процесса на объекте (захватке);
  
• 
  t_о (ij) – окончание процесса на объекте (захватке);
  
• 
  
  t_орг
  – величина простая объектов (захватки) между началом на них следующего процесса и окончанием предыдущего (называют организационным перерывом):
  

(1.1)

2. Окончание каждого процесса (ij) на объекте (захватке) j равно сумме его начала t_н(ij) и продолжительности t(ij), оно записывается в клетке справа вверху:

t_о(ij) = t_н(ij)+ t(ij). (1.2)

3. Начало каждого последующего процесса i+1 на каждом объекте (захватке) j может наступить не ранее срока окончания предыдущего процесса iна том же объекте (захватке) j.

t_н(i + 1) ,j t_о(ij). (1.3)

Задачи, решаемые матричным методом, методом Афанасьева:

1. 
   Организация беспростойного движения спецподразделений по объектам (захваткам).
   
2. 
   Определение времени окончания СМР на всем комплексе объектов, дн.
   
3. 
   Определение суммарного рабочего времени всех спецподразделений на каждом объекте t_{р.об., дн.} и суммарных по комплексу .
   
4. 
   Определение организационных простоев каждого объекта t_орг.об и суммы их по комплексу .
   
5. 
   Определение продолжительности строительства каждого объекта t_об.,дн. и суммы их по комплексу .
   
6. 
   Определение продолжительности занятости суммарного рабочего времени каждого спецподразделения на всем комплексе объектов t_{бр.к, дн.}.
   
7. 
   Определение коэффициента плотности К_пл..
   

Пример решения поставленных задач представлен в табл.1.3.

Таблица 1.3

Контрольный пример

организации неритмичного потока

(матричный метод, метод Афанасьева)

N n		Процессы (спецподразделения)				tр.об.,дн.	tорг.об.,дн.	tоб.,дн.
		1	2	11 3	15 4
Объекты (захватки)	I	0 3 3	3 7 (+4) 4	12 7 8 (+3) 1	19 12 16 4	12	7	19
	II	(+2) 3 5 2	(-2) 7 10 3	8 13 12 15 (+1) (+4) 3	16 18 19 21 2	10	8	18
	III	5 6 (+4) 1	10 14 4	13 18 4	18 20 1	10	7	17
	IV	(+4) 6 10 4	14 19 5	18 22 3	20 24 2	14	4	18
tбр. к, дн		10	16	11	9	tбр. к. =46	-	-
Rбр.к, чел.		4	8	6	10	-	-	-

Описание: 1-я задача – организация беспростойного движения бригад по всем объектам.

Начало первого процесса на объекте I равно 0, что и записываем в верхнем левом углу клетки матрицы (табл.1.3) t_н (1,1) = 0).

При продолжительности процессаt (1,1) = 3 дня его окончание t_о(1,1)=0+3=3.

Эта цифра переносится в верхний левый угол клетки матрицы, обозначающий начало работы 1-го процесса на объекте II, т.е. t_н(1,2)=3 и окончание этого процесса на объекте II при продолжительности t(1,2)=2, t_о(1,2)=3+2=5. Аналогичным образом рассчитаем начало и окончание работ первого процесса на объектах III и IV, т.е. движение 1-й бригады по всем четырем объектам (захваткам). Отмечаем, что 1-я бригада, выполняющая 1-й процесс, прошла все объекты без простоев.

Возможное время начала 2-го процесса на объекте I определяется временем окончания на этом объекте 1-го (предыдущего) процесса, т.е. t_н(2,1)= t_о(1,1)=3.

При продолжительности выполнения работ 2-го процесса на объекте I t(2,1)=4 время окончания соответственно t_о(2,1)=3+4=7.

Вторая бригада после выполнения работ на объекте I переходит на объект II. Отмечаем, что объект II после первого процесса уже готов был принять бригаду 2-го процесса 5-го дня и простоял в ожидании начала работы 2-го процесса 2 дня.

Фиксируем этот факт на линии раздела 1-го и 2-го процесса (+2). Знак плюс обозначает простои объекта, а цифра 2 – количество дней простоя. На контрольном примере видно, что 2-я бригада прошла все 4 объекта без простоя, в то же время зафиксированы простои объектов II, III, IV (+2); (+3); (+4) соответственно.

Возможное начало выполнения работ 3-го процесса (3-й бригады) определяется готовностью объекта I к этим видам работ, т.е. временем окончания работ 2-го (предыдущего) процесса:

По окончании выполнения работ 3-й бригадой на объекте I (t₀(3,1)=8) она перешла на объект II (t_н(3,2)=8), но готовность II объекта для выполнения 3-го процесса t₀(2,2)=10, т.е. 3-я бригада вынуждена ожидать 2 дня начала выполнения своей работы на объекте II. Эта ситуация фиксируется обозначением (-2) на линии раздела 2-го и 3-го процессов. Знак (-) обозначает простои бригады (спецподразделения). Цифра 2- время простоя в днях. Надо отметить, что начало работы 3-й бригадой на объекте II возможно только10-го, а не 8-го, поэтому окончание работ этой бригадой при продолжительности t(3,2)=3 дня будет t₀(3,2)=10+3=13. закончив работы на объекте II (t₀(3,2)=13), 3-я бригада перешла на объект III, который будет готов для выполнения 3-го процесса только t₀(2,3)=14, 3-я бригада опять вынуждена ожидать (простаивать) (-1) день, что так же, как и в предыдущем случае, фиксируется цифрой (-1) на линии раздела. Такая же ситуация ожидает эту бригаду и на объекте IV. За весь период выполнения работ на комплексе объектов 3-я бригада простояла в общей сложности 4 дня (2 дня на объекте II, 1 день на объекте III и 1 день на объекте IV).

Организация СМР с простоями рабочего персонала недопустима (нецелесообразна) как с экономической (снижение среднедневного заработка рабочего), так и с управленческой точек зрения.

Устранение простоев бригад при планировании осуществляется путем сдвижения начала ее работы на I объекте на время, равное сумме величин простоев на всех объектах, которые определились (зафиксировались) при первоначальном варианте расчета. В нашем контрольном примере зафиксирована сумма простоев 3-й бригадой t_бр.(3) = 4 дня, т.е. 3-й бригаде начало работ на первом объекте (t_н(3,1)) надо сдвинуть на 4 дня t_н(3,1)=t₀(2,1)+4=7+4=11. В этом случае 3-я бригада пройдет все объекты без простоев, что и показано на контрольном примере при повторном расчете. При этом необходимо зафиксировать все организационные простои объектов. Аналогично организуется беспростойная работа 4-й бригады.

Первая задача – организация беспростойного движения спецподразделений по объектам – выполнена путем сдвижения сроков начала работы 3-го и 4-го спецподразделений на объекте I на количество дней, равное сумме простоев этих подразделений, выявленных (определенных) при первоначальном расчете.

Вторая задача – определение продолжительности выполнения всех СМР на комплексе объектов Т₀ – выполнена путем расчета окончания работ на объекте IV 4-й операции (четвертым спецподразделением). В нашем примере t₀(4,4) = 24 дня, т.е. Т₀ = 24 дня.

Третья задача – определение продолжительности простоя каждого объекта (t_орг.об) решается путем сложения всех зафиксированных на линиях раздела процессов организационных простоев по каждому объекту. Так, на контрольном примере на объекте I сумма t_орг. I = 7 дн, на объекте II t_орг. II = 8 дн., 7 и 4 дн. соответственно на объектах III и IV.

Четвертая задача – определение количества рабочих дней СМР каждого объекта – выполняется путем сложения времени работы каждого процесса на объекте и фиксируется это в графе t_р.об.

В контрольном примере t_р.об. имеют значение 12, 10, 10, 14 на I, II, III, IV объектах соответственно.

Пятая задача – определение продолжительности строительно-монтажных работ каждого объекта t_об. = t_р.об.. + t_орг.об.. В контрольном примере эти значения фиксируются в графе матрицы t_об и имеют значения 19, 18, 17, 18.

Шестая задача – определение продолжительности работы каждого спецподразделения на всем комплексе объектов выполняется путем суммирования рабочего времени спецподразделений на всех объектах в строке t_бр.к и имеет значения 10, 16, 11, 9.

Выполняется контрольная проверка правильности (безошибочности) подсчета рабочих дней путем сравнивания суммы рабочих дней графы t_р.об. = 46 и суммы работ всех бригад на всем комплексе объектов t_бр.к=46.

Седьмая задача – определение коэффициента плотности. Большое значение при организации СМР имеет показатель коэффициента плотности, т.е. степени совмещения работ и использования фронта работ в неритмичном потоке. Этот показатель определяется путем деления суммы рабочих дней на всех объектах (t_р.об. = 46 дн.) на сумму общего времени СМР (t_об. = 72 дн.). Для полученных исходных данных – это максимально возможное совмещение работы бригад (спецподразделений) при постоянном их составе. Коэффициент плотности К_пл. графика в контрольном примере оказался невысоким – 0,64.

. (1.4)

2.