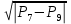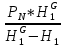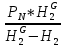|
|
компьютерное моделирование хтп. Цветкова Ирина тм 43 дз1. Практическая работа 1 По курсу Компьютерное моделирование химикотехнологических процессов
Российский химико-технологический университет
Д. И. Менделеева
Практическая работа №1
По курсу
«Компьютерное моделирование химико-технологических процессов»
«Компьютерное моделирование простой гидравлической системы в статическом режиме»
Группа ТМ-43
Студентка: Цветкова Ирина
Вариант 20
Проверила: Шумакова О. П.
Москва 2020
Изображение гидравлической системы с заданными направлениями движениями жидкости:
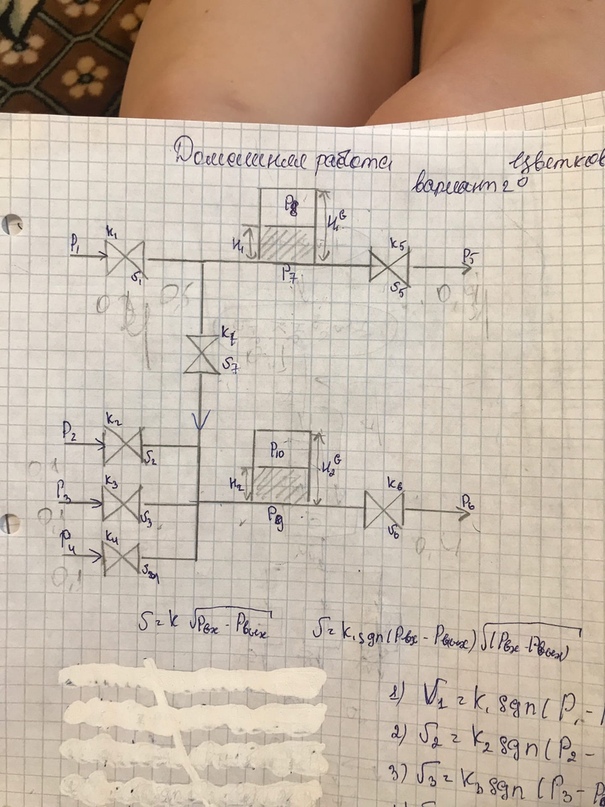
Основные обозначения:
P1 – P4 - давление жидкости на входе в систему;
P5, P6 – давление жидкости на выходе из системы;
P7, P9 – давление жидкости на дно емкости;
P8, P10 – давление жидкости внутри емкости;
V1 – V7 – скорости потока;
k1 – k7 – коэффициент пропускной способности клапана;
H1, H2 – высота столба жидкости в емкости;
H1G, H2G – геометрическая высота емкости.
. Построение системы уравнений математического описания (МО) гидравлической системы
Определение скорости потоков жидкости через клапаны:
V = k * 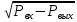
V = k * sgn (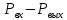 ) )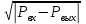
V1 = k1 * sgn (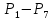 ) )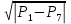
V2 = k2 * sgn (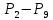 ) )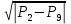
V3 = k3 * sgn (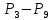 ) )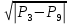
V4 = k4 * sgn (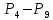 ) )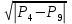
V5 = k5 * sgn (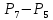 ) )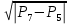
V6 = k6 * sgn (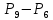 ) )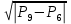
V7 = k7 * sgn (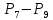 ) )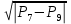
Расчет балансов (уравнение материального баланса):
8. V1 -V7– V5 = 0
9. V7+ V2 +V3 + V4 – V6 = 0
Определение давления жидкости и газа в закрытых емкостях
10. P7 = P8 + ρgH1
11. P8 = 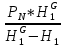
12. P9 = P10 + ρgH2
13. P10 = 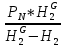
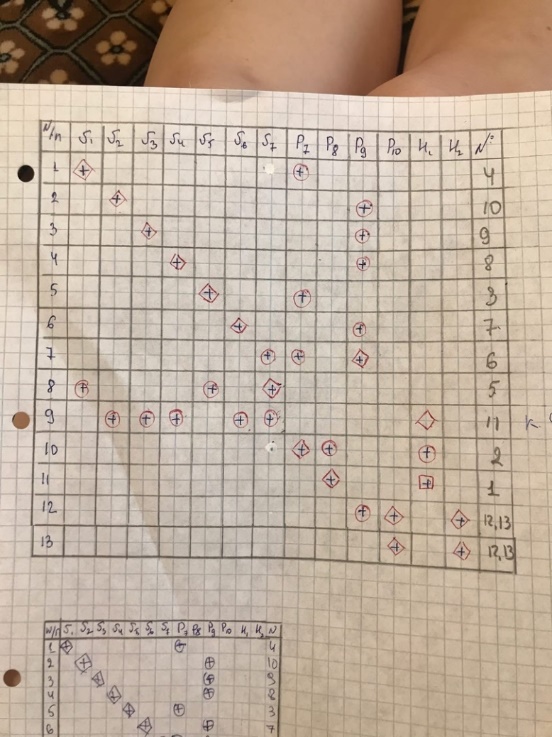
Информационная матрица имеет вид:
Блок-схема расчёта:
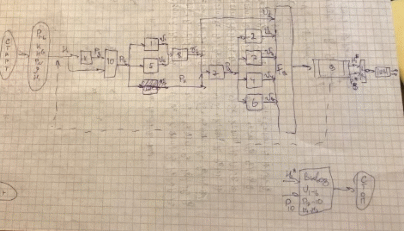
Программа:
Функция
function fx=func(x)
global np
global nk
global nv
global ro
global pn
global p
global ak
global vm
global h
global hg
global g
global v
% уравнения записываются в соответсвии последовательности в информационной матрице
h(1) = x;
p(8) = pn * hg(1) / (hg(1) - h(1));
p(7) = p(8) + ro * g * h(1);
v(1) = ak(1) * sign(p(1) - p(7)) * sqrt(abs (p(1) - p(7)));
v(5) = ak(5) * sign(p(7) - p(5)) * sqrt(abs (p(7) - p(5)));
v(7) = v(1) - v(5);
p(9) = p(7) - sign(v(7)) * (v(7) / ak(7)) ^ 2;
v(6) = ak(6) * sign(p(9) - p(6)) * sqrt(abs (p(9) - p(6)));
v(2) = ak(2) * sign(p(2) - p(9)) * sqrt(abs (p(2) - p(9)));
v(3) = ak(3) * sign(p(3) - p(9)) * sqrt(abs (p(3) - p(9)));
v(4) = ak(4) * sign(p(4) - p(9)) * sqrt(abs (p(4) - p(9)));
% корректирующее уравнение
fx = (v(2) + v(3) + v(4) - v(6) + v(7)) * ro;
end
Программа
clc
global np
global nk
global nv
global ro
global pn
global p
global ak
global vm
global h
global hg
global g
global v
disp ('Статика')
disp ('Ввод исходных данных')
% np-количество давлений (всего); nk-количество вентелей; nv-количество уравнений
np=10; nk=7; nv=13; hg= [10, 10]; ro=1181;
disp ('Высота емкостей'); disp (hg(1:2));
disp ('плотность (кг/м3)'); disp (ro);
% давление вводить в системе СИ
disp ('Начальное давление (Па)'); pn=100000;
% неизвестные давления отмечены в блоке ввода нулями
% чтобы жидкость шла в выбранном направлении давления на входе должно быть больше, чем давление на выходе
% именно поэтому p1= 0.5 МПа,а p2= 0.25 МПа,p3= 0.25 МПа, p4= 0.25 МПа
disp ('Давление (1-6 7-10)'); p=[700000, 1000000, 1000000, 1000000, 500000, 500000, 0, 0, 0, 0];
disp ('Коэф. пропускной способности (1-7)'); k=[0.05, 0.01, 0.01, 0.01, 0.02, 0.06, 0.03];
disp ('Относительнная локальная погрешность (%)'); e=0.1;
disp ('Площадь внутренного проходного сечения трубопровода (м^2)'); S=0.01;
%перевод коэффициента открытия вентиля в величину, имеющую размерность
for i=1:7
ak(i)=k(i)*S/sqrt(ro);
end
g=9.815; e=e/100; a=0; b=hg(1) * (1-e);
fa=func(a); fb=func(b);
if sign(fb) = sign(fa)
%поиск нуля функции стандартной функцией пакета MATLAB
h(1)=fzero('func(x)', [a,b]);
%
a = -ro * g; b = p(9) + ro * g * hg(2);
c = (pn - p(9)) * hg(2);
h(2) = (-b + sqrt(b * b - 4 * a * c)) / (2 * a);
p(10) = pn * hg(2) / (hg(2) - h(2));
vm = v * ro;
disp('Результат h p vm');
disp(h(1:2)); disp(p(1:10)); disp(v(1:7));
else
disp('Решения нет')
end
Результат введенных данных:
Н1 = 8.1921 м, Н2 = 8,1430 м
Р7
|
Р8
|
Р9
|
Р10
|
0.6481*106 Па
|
0.531*106 Па
|
0.6329*106 Па
|
0.5385*106 Па
|
V1
|
V2
|
V3
|
V4
|
V5
|
V6
|
V7
|
0.0033
|
0.0018
|
0.0018
|
0.0018
|
0.0022
|
0.0064
|
0.0011
|
Рассчетные исследования компьютерной модели.
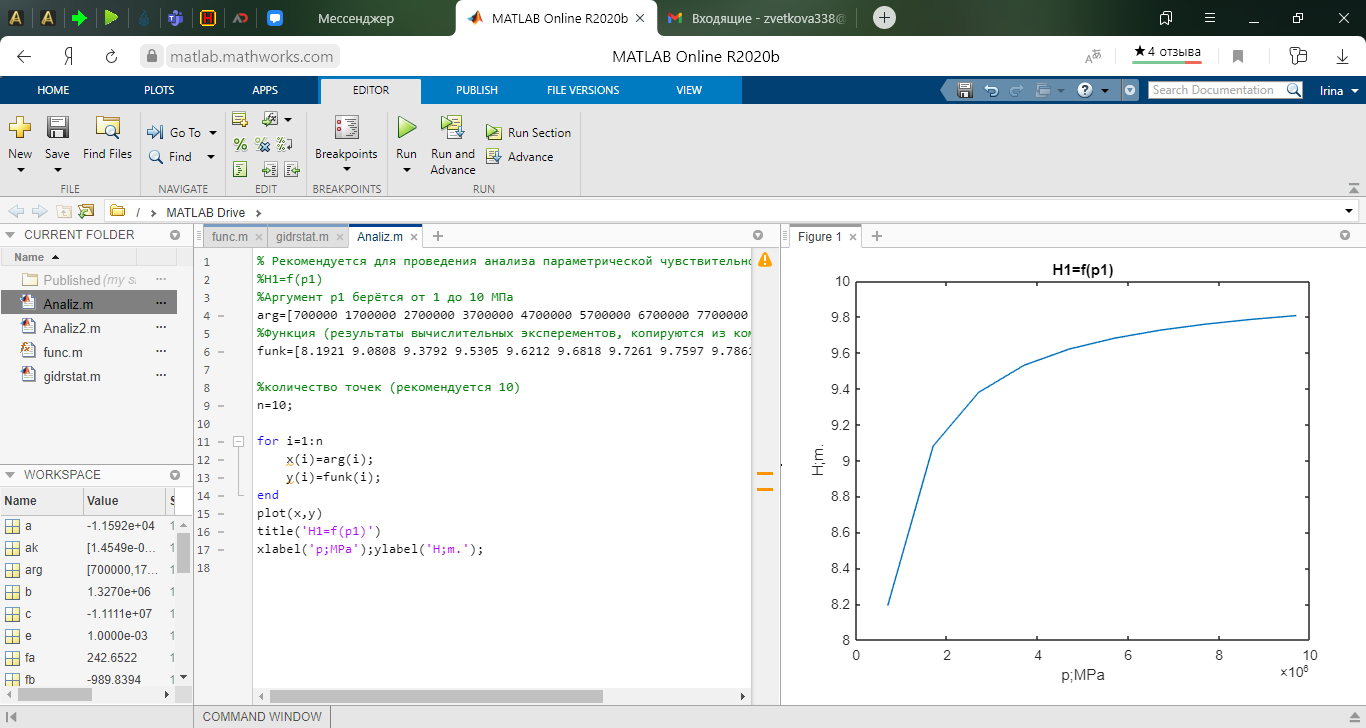
% Рекомендуется для проведения анализа параметрической чувствительности
%H1=f(p1)
%Аргумент р1 берётся от 0.7 до 9.7 МПа
arg=[700000 1700000 2700000 3700000 4700000 5700000 6700000 7700000 8700000 9700000 ];
%Функция (результаты вычислительных эксперементов, копируются из командного окна пакета МАТЛАБ
funk=[8.1921 9.0808 9.3792 9.5305 9.6212 9.6818 9.7261 9.7597 9.7861 9.8073];
%количество точек (рекомендуется 10)
n=10;
for i=1:n
x(i)=arg(i);
y(i)=funk(i);
end
plot(x,y)
title('H1=f(p1)')
xlabel('p;MPa');ylabel('H;m.');
Анализ параметрической чувствительности статической модели к изменению входного давления Р1.
%Рекомендуется для проведения анализа параметрической чувствительности
%H2=f(p6)
%Аргумент р6 берётся от 100 до 190 кПа
arg=[100000 110000 120000 130000 140000 150000 160000 170000 180000 190000];
% Функция (результаты вычислительных эксперементов, копируются из командного окна пакета МАТЛАБ
funk=[8.6931 8.6939 8.6946 8.6954 8.6961 8.6969 8.6977 8.6984 8.6992 8.7000];
% количество точек (рекомендуется 10)
n=10;
for i=1:n
x(i)=arg(i);
y(i)=funk(i);
end
plot(x,y)
title('H2=f(p6)')
xlabel('p;кPa');ylabel('H;m.');
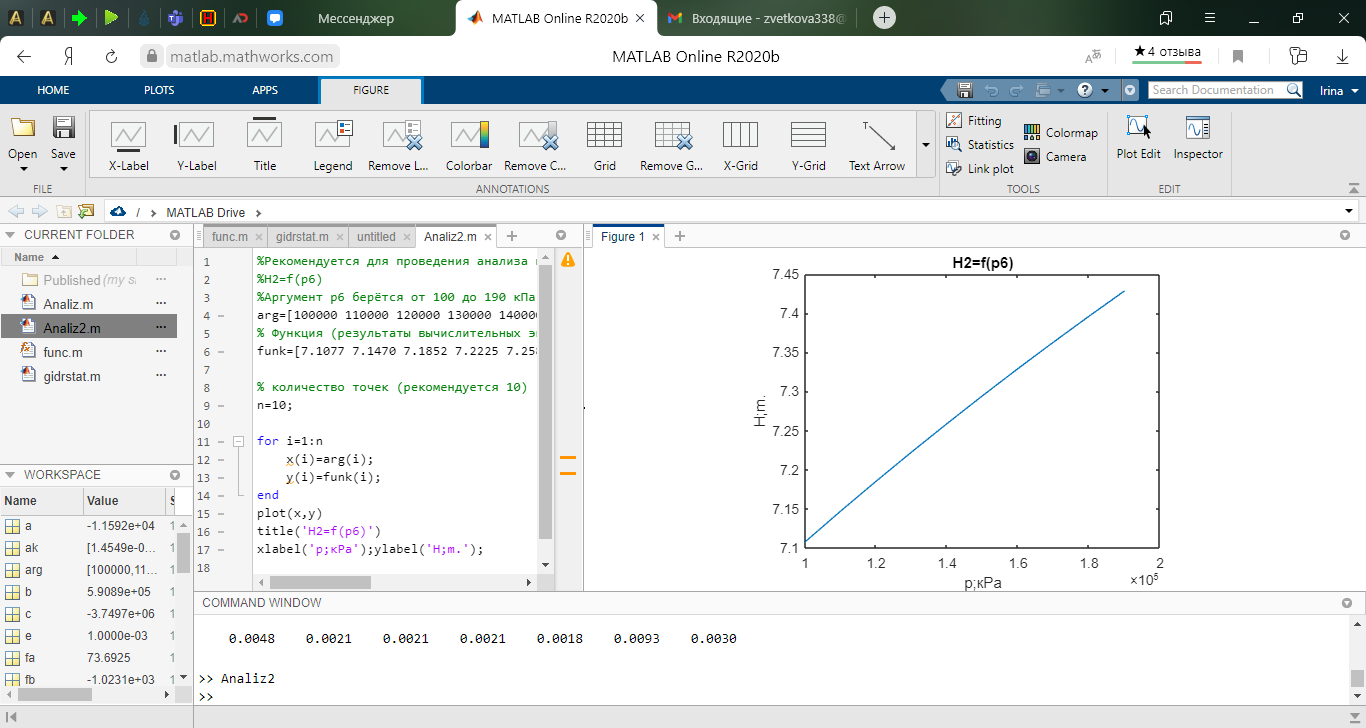
Анализ параметрической чувствительности статической модели к изменению выходного давления Р6.
%Рекомендуется для проведения анализа параметрической чувствительности
%H2=f(p6)
%Аргумент р6 берётся от 100 до 190 кПа
arg=[100000 110000 120000 130000 140000 150000 160000 170000 180000 190000];
% Функция (результаты вычислительных эксперементов, копируются из командного окна пакета МАТЛАБ
funk=[7.1077 7.1470 7.1852 7.2225 7.2589 7.2945 7.3292 7.3630 7.3961 7.4284];
% количество точек (рекомендуется 10)
n=10;
for i=1:n
x(i)=arg(i);
y(i)=funk(i);
end
plot(x,y)
title('H2=f(p6)')
xlabel('p;кPa');ylabel('H;m.');
Вывод:
В практической работа №1:
Исследовали систему уравнений математического описания (МО) заданной гидравлической системы в стационарном режиме;
Сформировали информационную матрицу системы уравнений МО и составили блок-схему оптимального моделирующего алгоритма расчёта системы уравнений МО стационарной гидравлической системы;
Написали для данной системы программу MATLAB для расчёта высоты столба жидкости в ёмкости, скоростей потока, а также давления жидкости на дно ёмкости и внутри её;
Построены зависимости высоты жидкости в ёмкости от входных и выходных давлений. Можно сделать вывод, что с увеличением давления (входного и выходного) высоты жидкости возрастает.
|
|
|
 Скачать 0.71 Mb.
Скачать 0.71 Mb.



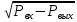
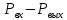 )
)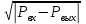
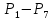 )
)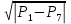
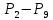 )
)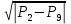
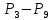 )
)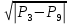
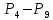 )
)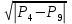
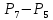 )
)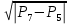
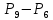 )
)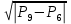
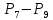 )
)