Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Магнитогорский государственный технический университет им. Г.И. Носова»
Практическая работа № 1 по курсу
Управленческий учет и учет персонала
Выполнил: Грыжук Юлия Валериевна
Гр: дЭУПп-19
Проверил:
Магнитогорск, 2022
Выполнить дифференциацию (деление) затрат на постоянные и переменные методом регрессионного анализа по исходным данным представленным в табл. 1. Выполнение регрессионного анализа предполагается в 2 этапа: 1) выполнение регрессионного анализа по исходным затратам 2) выполнение регрессионного анализа по скорректированным затратам Оценить статистическую значимость полученного уравнения регрессии и построить доверительный коридор (см. справочный материал).
Для выполнения задания рекомендуется использовать пакет электронных таблиц MS Excel.
Таблица 1- Исходные данные для выполнения регрессионного анализа
Период
(№ квартала)
|
Объем производства, т
|
Затраты, руб.
|
Исходные
|
Скорректированные[1]
|
1
|
212
|
5 219 940
|
13 381 668
|
2
|
227
|
5 521 441
|
14 197 900
|
3
|
226
|
5 486 545
|
14 122 564
|
4
|
213
|
5 259 420
|
13 459 882
|
5
|
213
|
5 467 422
|
13 398 426
|
6
|
230,3
|
5 832 076
|
14 367 543
|
7
|
228,3
|
5 769 665
|
14 227 015
|
8
|
217,8
|
6 694 805
|
13 754 288
|
9
|
220
|
8 597 109
|
13 845 368
|
10
|
228,8
|
9 250 267
|
14 254 026
|
11
|
230,3
|
9 697 312
|
14 338 587
|
12
|
214
|
9 297 747
|
13 458 776
|
13
|
203,5
|
8 823 660
|
12 774 051
|
14
|
230,3
|
11 170 425
|
14 374 295
|
15
|
230,3
|
12 368 082
|
14 372 229
|
16
|
201,2
|
11 782 888
|
12 764 781
|
17
|
203,5
|
12 194 835
|
12 811 515
|
18
|
230,3
|
14 082 369
|
14 400 832
|
19
|
230,3
|
14 063 623
|
14 380 586
|
20
|
227,3
|
14 197 283
|
14 227 401
|
Период
|
Х -Объем
производства, т
|
Y - Затраты, руб.
|
Х-Хср
|
(Х-Хср)^2
|
(№ квартала)
|
Исходные
|
Скорректированные
|
|
|
1
|
212,00
|
5219940,00
|
13381668,00
|
-8,86
|
78,50
|
2
|
227,00
|
5521441,00
|
14197900,00
|
6,14
|
37,70
|
3
|
226,00
|
5486545,00
|
14122564,00
|
5,14
|
26,42
|
4
|
213,00
|
5259420,00
|
13459882,00
|
-7,86
|
61,78
|
5
|
213,00
|
5467422,00
|
13398426,00
|
-7,86
|
61,78
|
6
|
230,30
|
5832076,00
|
14367543,00
|
9,44
|
89,11
|
7
|
228,30
|
5769665,00
|
14227015,00
|
7,44
|
55,35
|
8
|
217,80
|
6694805,00
|
13754288,00
|
-3,06
|
9,36
|
9
|
220,00
|
8597109,00
|
13845368,00
|
-0,86
|
0,74
|
10
|
228,80
|
9250267,00
|
14254026,00
|
7,94
|
63,04
|
11
|
230,30
|
9697312,00
|
14338587,00
|
9,44
|
89,11
|
12
|
214,00
|
9297747,00
|
13458776,00
|
-6,86
|
47,06
|
13
|
203,50
|
8823660,00
|
12774051,00
|
-17,36
|
301,37
|
14
|
230,30
|
11170425,00
|
14374295,00
|
9,44
|
89,11
|
15
|
230,30
|
12368082,00
|
14372229,00
|
9,44
|
89,11
|
16
|
201,20
|
11782888,00
|
12764781,00
|
-19,66
|
386,52
|
17
|
203,50
|
12194835,00
|
12811515,00
|
-17,36
|
301,37
|
18
|
230,30
|
14082369,00
|
14400832,00
|
9,44
|
89,11
|
19
|
230,30
|
14063623,00
|
14380586,00
|
9,44
|
89,11
|
20
|
227,30
|
14197283,00
|
14227401,00
|
6,44
|
41,47
|
среднее Х:
|
220,86
|
|
|
сумма:
|
2007,15
|
1) выполнение регрессионного анализа по исходным затратам
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
Множественный R
|
0,997534293
|
|
|
R-квадрат
|
0,995074666
|
|
|
Нормированный R-квадрат
|
0,994801037
|
|
|
Стандартная ошибка
|
41956,62257
|
|
|
Наблюдения
|
20
|
|
|
Дисперсионный анализ
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
1
|
6,40167E+12
|
6,40167E+12
|
3636,57483
|
3,17074E-22
|
Остаток
|
18
|
31686447197
|
1760358178
|
|
|
Итого
|
19
|
6,43336E+12
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Y-пересечение
|
1372493,819
|
207049,5002
|
6,628819761
|
3,19111E-06
|
937498,9602
|
Переменная X 1
|
56475,11017
|
936,5065572
|
60,30402001
|
3,17074E-22
|
54507,5829
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
|
|
1807488,677
|
937498,9602
|
1807488,677
|
|
|
|
58442,63743
|
54507,5829
|
58442,63743
|
|
|
|
2) выполнение регрессионного анализа по скорректированным затратам
|
|
|
|
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
Множественный R
|
0,997534293
|
|
|
R-квадрат
|
0,995074666
|
|
|
Нормированный R-квадрат
|
0,994801037
|
|
|
Стандартная ошибка
|
41956,62257
|
|
|
Наблюдения
|
20
|
|
|
Дисперсионный анализ
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
1
|
6,40167E+12
|
6,40167E+12
|
3636,57483
|
3,17074E-22
|
Остаток
|
18
|
31686447197
|
1760358178
|
|
|
Итого
|
19
|
6,43336E+12
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Y-пересечение
|
1372493,819
|
207049,5002
|
6,628819761
|
3,19111E-06
|
Переменная X 1
|
56475,11017
|
936,5065572
|
60,30402001
|
3,17074E-22
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
|
937498,9602
|
1807488,677
|
937498,9602
|
1807488,677
|
|
|
54507,5829
|
58442,63743
|
54507,5829
|
58442,63743
|
|
|
доверительный коридор
|
|
|
|
|
|
|
Доверительный интервал (Для уровня значимости α = 0,05 и объеме выборки n = 7 (число степеней свободы df =7 − 2 = 5) tтабл = 2,57.):
|
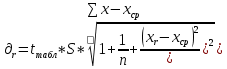
S2 – остаточная дисперсия на одну степень свободы (S2 = 2,27).
|
|
|
|
|
Доверительные границы (доверительный интервал) для уравнения регрессии:
|
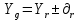
|
|
|
где Yr − значения уравнения регрессии;
|
|
Yg− Значения доверительного интервала;
|
|
∂r− доверительный интервал (отклонения от уравнения регрессии).
Расчет доверительных границ уравнения регрессии
|
|
|
|
|
|
|
|
|
|
1. Рассчитываем в таблице с исходными данными с помощью функций Excel
|
|
|
|
|
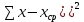 = 2007,15 = 2007,15
|
| |
 Скачать 27.84 Kb.
Скачать 27.84 Kb.

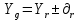
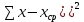 = 2007,15
= 2007,15