Практические работы 5 кл по математике. Практическая работа 1 Построение узора из окружностей Практическая работа 2 Построение углов
 Скачать 1.24 Mb.
|
|
Комплект практических работ по математике. 5 класс Практическая работа №1 «Построение узора из окружностей» Практическая работа №2 «Построение углов» Практическая работа №3 «Построение прямоугольника с заданными сторонами на нелинованной бумаге» Практическая работа № 4 «Куб. Изображение куба» Практическая работа №5 «Площадь поверхности прямоугольного параллелепипеда» Практическая работа №1 «Построение узора из окружностей» Цели работы: Знакомство с геометрическими фигурами - окружность и круг. Изучение элементов окружности. Измерение радиусов окружности и круга. Построение окружности и круга. Построение узора из окружностей. Оборудование: циркуль, линейка, карандаш. Ход работы П 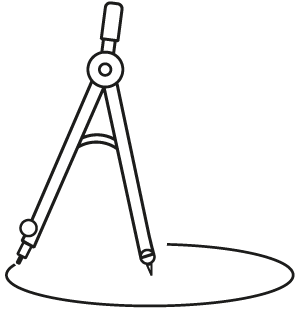 ознакомьтесь с алгоритмом построения окружности и изучите ее свойства.Поставьте на листе тетради точку. Обозначь ее буквой О. Возьмите циркуль в руки следующим образом: ножку циркуля с иглой установи в точку О, а ножку циркуля с грифелем вращайте вокруг данной точки, касаясь листа тетради. Циркуль опишет замкнутую линию. Ее называют окружностью. Точку О называют центром окружности. Отметьте точку А на окружности и проведите отрезок, соединяющий точку А и центр окружности точку - О, такой отрезок называется радиус. Постройте радиус ОВ.
Ответьте на вопросы и выполните задание: Сколько радиусов можно провести в одной окружности? Сравните длины этих отрезков. Сделайте вывод, запишите его в тетрадь. Постройте отрезок МК, соединяющий две точки окружности, который проходит через её центр, такой отрезок называется диаметр. Построй диаметр РТ.
Ответьте на вопросы и выполните задание: Сколько диаметров можно провести в одной окружности? С 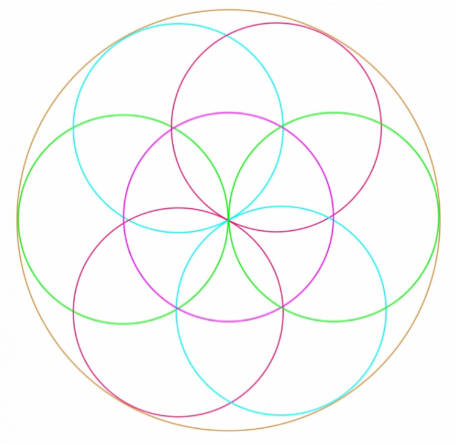 равните длину диаметра с длиной радиуса.Сделайте вывод. Запишите вывод в тетрадь. Нарисуйте окружность. Не меняя радиуса, переставьте ножку циркуля с иглой в любую точку на окружности и снова нарисуйте окружность. Точки пересечения этих окружностей станут центрами новых окружностей. Внутри основного круга появился цветок. Контрольный вопрос: Что можно сказать о расположении точек окружности по отношению к центру окружности? Дополнительные вопросы и задания: Нарисуйте две окружности, которые не пересекаются. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь. Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь. Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите в тетрадь. Приведите примеры окружности и круга в окружающих вас предметах. Практическая работа №2 «Построение углов» Цели работы: Познакомиться с алгоритмом построения угла заданной градусной меры. Научиться строить угол заданной градусной меры. Научиться определять вид угла. Оборудование: транспортир, линейка, карандаш. Ход работы П 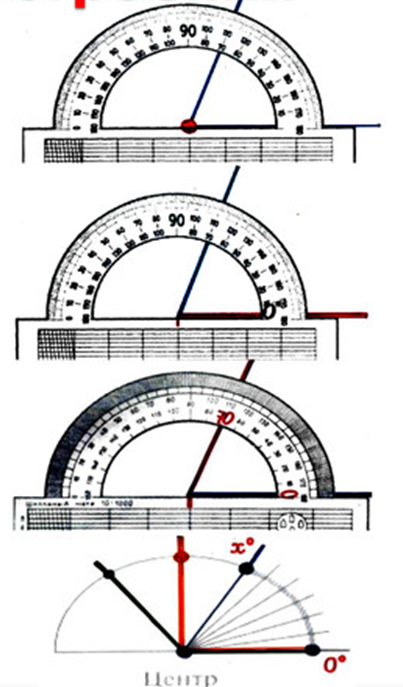 ознакомьтесь с алгоритмом построения углов с помощью транспортира.Отметьте вершину угла точку - О. Постройте луч с началом в точке О. Совместите вершину угла с центром транспортира. Расположите транспортир так, чтобы построенная сторона угла проходила через начало отсчета на шкале транспортира (совместите с 00). Найди на шкале транспортира деление, соответствующее данной градусной мере, сделайте метку карандашом. Постройте луч с началом в точке О, проходящий через метку. Проверьте, соответствует ли градусная мера построенного угла его виду (острый, прямой, тупой, развернутый). Выполните построение заданных углов и заполните таблицу.
Дополнительные вопросы и задания: При помощи линейки и чертежного угольника с углами 300, 600, 900 и углами 450, 450, 900 можно построить любой угол, кратный 150. 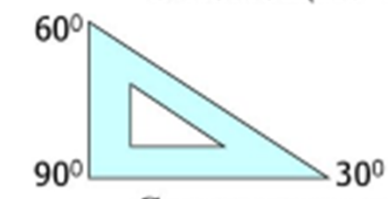 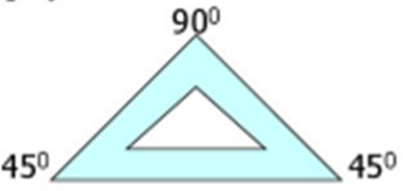 Схемы построения углов  Выполните задание: постройте с помощь чертежных треугольников угол, равный 1650. Практическая работа №3 «Построение прямоугольника с заданными сторонами на нелинованной бумаге» Цели работы: Познакомиться с алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге. Научиться строить прямоугольник с заданными сторонами на нелинованной бумаге. Оборудование: чертёжный угольник, линейка, карандаш. Ход работы Познакомьтесь с алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге. 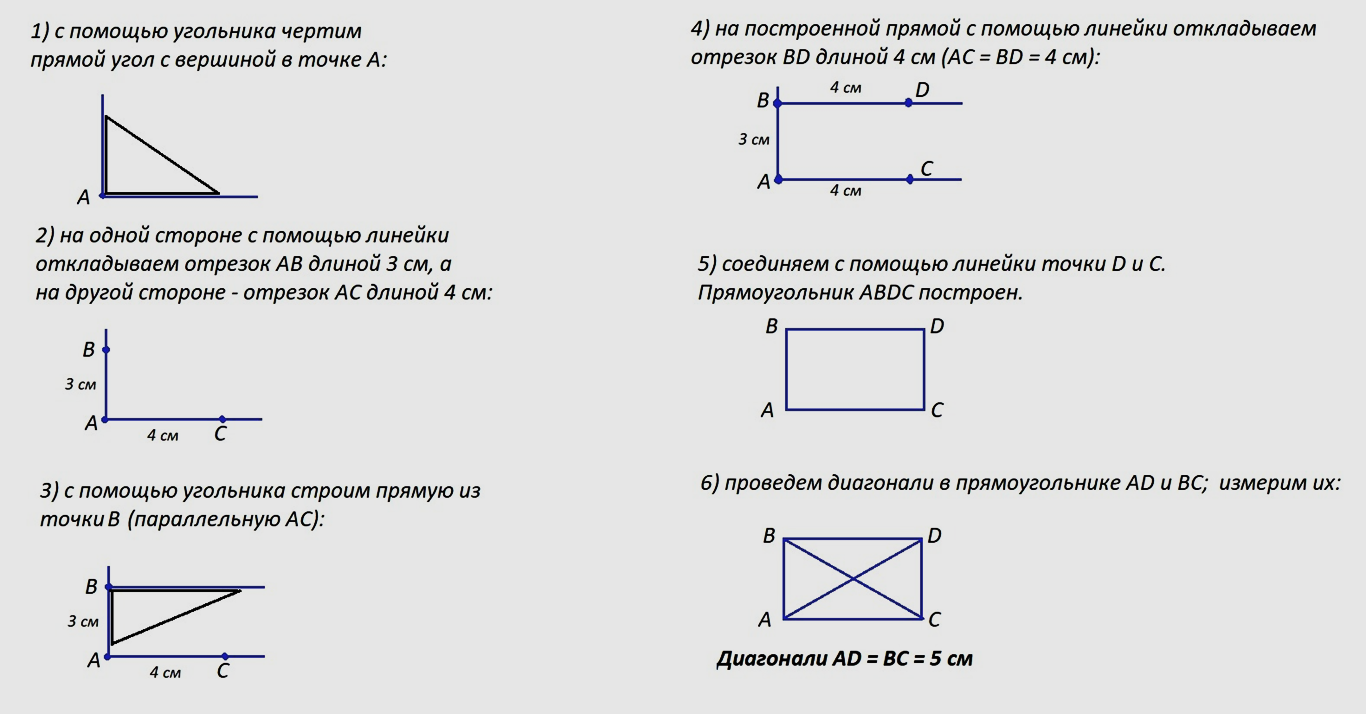 Выполните построение прямоугольника ABCD с указанными длинами сторон и проведите в нем диагонали, заполните таблицу.
Контрольный вопрос: Сравните длины диагоналей, сделайте вывод, запишите его в тетрадь. Дополнительное задание: Вычислите периметр и площадь получившегося прямоугольника. Практическая работа №4 «Куб. Изображение куба» Цели работы: Изучить геометрическую объёмную фигуру куб. Определить сколько граней, рёбер, вершин. Определить размеры рёбер и углов. Определить форму граней. Выяснить, какие предметы окружающего мира имеют форму куба. Научиться чертить куб. Оборудование: кубики, линейка Ход работы. Рассмотрите внимательно фигуру. Пересчитайте грани куба. Грань куба - это стороны куба. Сколько их? Запишите ответ в тетрадь. Покажите боковые грани куба. Сколько их. Запишите в тетрадь. Покажите верхнюю грань. Сколько их. Запишите. Покажите нижнюю грань куба. Сколько их. Запишите. Какой геометрической фигурой является грань куба? Запишите ответ. Пересчитайте все рёбра куба. Ребро куба – это отрезок, соединяющий 2 грани. Сколько рёбер в кубе? Запишите ответ в тетрадь. Равны ли рёбра по длине? Запишите в тетрадь. Верно ли, что каждые две грани имеют общее ребро? Запишите ответ. Сколько вершин у куба? Вершина куба– это угол куба. Запишите в тетрадь. Сколько рёбер пересекаются (сходятся) в одной вершине? Запишите в тетрадь. Какие углы в кубе (острые, прямые, тупые)? Запишите в тетрадь. Определите, куб - это плоская или объёмная фигура? Объясните. Запишите ответ в тетради. Научитесь чертить куб в тетради. Выполните действия по порядку: Чертим квадрат со стороной 2 см. Отмечаем точки – вершины. От верхней левой вершины проводим диагональ через 2 клетки направо вверх. Отмечаем вершину точкой. Проводим 2см направо и отмечаем вершину. Соединяем эту вершину с верхним правым углом квадрата. Получилась верхняя грань куба. От нижнего правого угла квадрата проводим диагональ через 2 клетки направо вверх. Отмечаем вершину. Ведём 2 см вверх и соединяем точки. Получилась боковая грань куба. Это видимые грани. Сколько их? Невидимые рёбра проводим пунктирной (прерывистой) линией. Находим нижнюю левую точку первоначального квадрата. От неё проводим диагональ через 2 клетки направо вверх пунктиром. Отмечаем вершину. Ведём пунктир вверх до вершины. Самостоятельно проведите ещё одно невидимое ребро. Сверьте ответы с образцом и оцените свою работу. За каждый правильный ответ 1 балл. За правильный чертёж куба 3 балла. 13-15 баллов – оценка «5» 10-12 баллов - оценка «4» 6-9 баллов – оценка «3» 0-5 баллов – оценка «2» Практическая работа №5 «Площадь поверхности прямоугольного параллелепипеда» Цели работы: Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда. Научиться вычислять площадь поверхности куба и площадь поверхности прямоугольного параллелепипеда. Оборудование:прямоугольные параллелепипеды, кубики, линейка. Ход работы И 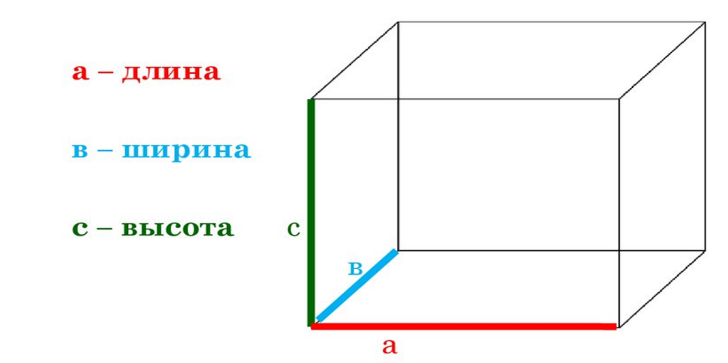 змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).Вычислите площадь полной поверхности прямоугольного параллелепипеда. S=2(ab + bc + ac) Вычислите площадь полной поверхности куба. S=6a2 Сделайте вычисления. Перенесите таблицу в тетрадь и заполните её.
Контрольные вопросы: Что можно сказать о противоположных гранях прямоугольного параллелепипеда? Сделайте вывод, запишите его в тетрадь. Что можно сказать о гранях куба? Сделайте вывод, запишите его в тетрадь. Дополнительные вопросы и задания: 1. Выразите: а) в кубических дециметрах: 5 м3 680 см3; 7 м3 15 см3; б) в кубических сантиметрах: 4 дм3 536 см3; 2 дм3 80 см3. 2. Сколько кубиков с ребром 10 см необходимо взять, чтобы построить башню длиной 25 м, шириной 6 м и высотой 100 м? |