вспвапфапыф. Практическая работа 1 Применение алгоритма Евклида для нахождения нод. Решение линейных диофантовых уравнений

• Название: Практическая работа 1 Применение алгоритма Евклида для нахождения нод. Решение линейных диофантовых уравнений
• Анкор: вспвапфапыф
• Дата: 25.10.2022
• Размер: 124.59 Kb.
• Имя файла: MU_MDK02_02_1-1.docx
• Тип: Практическая работа; #754456

ПРАКТИЧЕСКАЯ РАБОТА № 1

Применение алгоритма Евклида для нахождения НОД. Решение линейных

диофантовых уравнений

Цель: научиться решать линейные диофантовые уравнения с двумя неизвестными, используя алгоритм Евклида.

Теоретические вопросы

1. 
   Алгоритм Евклида для нахождения НОД.
   
2. 
   Понятие неопределенного уравнения.
   
3. 
   Понятие диофантового уравнения.
   
4. 
   Понятие линейного диофантового уравнения.
   
5. 
   Алгоритм решения линейных диофантовых уравнений.
   

Задание 1. Повторить алгоритм Евклида. Как с помощью алгоритма Евклида найти НОД двух чисел?

Задание 2. Найти НОД и его линейное выражение: а) НОД(11,8);

б) НОД(654,792);

в) НОД(3660,525);

г) НОД(400,288);

д) НОД(490,518);

е) НОД(510,272).

Задание 3. Приведите определение неопределенного уравнения.

Задание 4. Приведите определение диофантового уравнения.

Задание 5. Приведите примеры линейных дтофантовых уравнений. Задание 6. Изучите пример решения линейного диофантового уравнения: Решить уравнение 11х + 13у = 300 в натуральных числах.

1. 
   НОД(11,13) = 1.
   
2. 
   Находим линейное разложение 1 = 11·6 + 13·(–5).
   
3. 
   Умножаем обе части на 300, получаем
   

4. 
   Найдём решение в натуральных числах, для этого решим систему неравенств: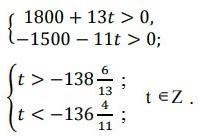
   

Таким образом, получаем два целых решения системы t = –138 и t = –137. Найдём решения задачи для полученных значений t.

При t = –138 х = 6, у = 18.

При t = –137 х = 19, у = 7.

Задание 7. Решить уравнения в целых числах:



Задание 7. Решите диофантово уравнение при помощи линейного представления НОД:

ПРАКТИЧЕСКАЯ РАБОТА № 2 Проверка чисел на простоту

Цель: научиться проверять числа на простоту.

Теоретические вопросы

1. 
   Понятие простого числа.
   
2. 
   Способы проверки числа на простоту.
   

Задание 1. Изучите способ проверки числа на простоту «Пробное деление».

Словесное описание: способ состоит в последовательном делении числа на все нечетные числа, которые содержатся в интервале. Если в процессе деления получим целый результат, то число составное. Если же при переборе всех нечетных чисел из интервала разделить число на эти числа нацело нельзя, то число простое (рисунок 1).

Программная реализация на языке С++: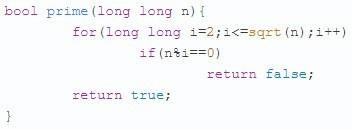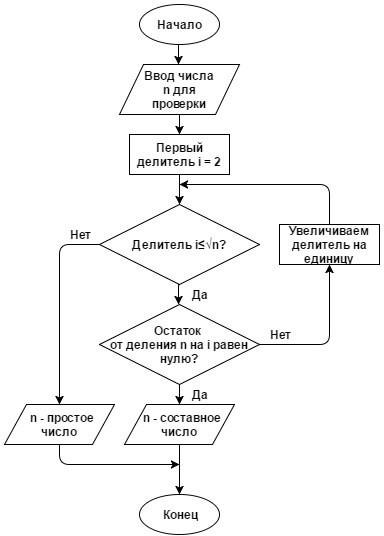





Рисунок 1 – Схема алгоритма

Задание 2. Изучите вероятностный алгоритм проверки на простоту числа «Тест на основе малой теоремы Ферма».

Малая теорема Ферма утверждает, что если n простое, то выполняется условие: при всех a из {1, 2, …, n−1} имеет место сравнение:

aⁿ⁻¹ ≡ 1 (mod n) (1)

Из этой теоремы следует, что если сравнение (1) не выполнено хотя бы для одного числа a в интервале {1, 2, …, n−1}, то n — составное. Поэтому можно предложить следующий вероятностный тест простоты.

1. 
   выбираем случайное число a из {1, 2, …, n−1} и проверяем с помощью алгоритма Евклида условие (a, n) = 1;
   
2. 
   если оно не выполняется, то ответ «n — составное»;
   
3. 
   проверяем выполнимость сравнения (1);
   
4. 
   если сравнение не выполнено, то ответ «n — составное»;
   
5. 
   если сравнение выполнено, то ответ неизвестен, но можно повторить тест еще раз.
   

Рисунок 2. Схема алгоритма Программная реализация на языке С++:



Нахождение НОД:



Быстрое возведение в степень по модулю:



Задание 3. Проверьте числа 11, 27, 119 на простоту с помощью представленных алгоритмов.

Задание 4. Изучите алгоритм проверки на простоту числа «Решето Эратосфена». Постройте схему алгоритма.

ПРАКТИЧЕСКАЯ РАБОТА № 3

Решение задач с элементами теории чисел.

Цель: решение задач с элементами теории чисел.

Теоретические вопросы

1. 
   Делимость чисел. Признаки делимости. Простые и составные числа.
   
2. 
   Основная теорема арифметики. Наибольший общий делитель. Взаимно простые числа.
   

Алгоритм Евклида для нахождения НОД.

3. 
   Отношения сравнимости. Свойства сравнений. Модулярная арифметика.
   
4. 
   Мультипликативные функции. Примеры мультипликативных функций.
   
5. 
   Классы. Полная и приведенная система вычетов. Функция Эйлера. Теорема ФермаЭйлера. Алгоритм быстрого возведения в степень по модулю.
   
6. 
   Сравнения первой степени. Линейные диофантовы уравнения. Расширенный алгоритм Евклида.
   
7. 
   Китайская теорема об остатках.
   
8. 
   Проверка чисел на простоту. Алгоритмы генерации простых чисел. Метод пробных делений. Решето Эратосфена.
   
9. 
   Разложение числа на множители. Алгоритмы факторизации. Факторизация Ферма. Метод Полларда.
   
10. 
    Алгоритмы дискретного логарифмирования. Метод Полларда. Метод Шорра.
    
11. 
    Арифметические операции над большими числами.
    

Задание 1. Найти все простые числа, не превосходящие 60.

Задание 2. Разложить на простые множители n = 29359.

Задание 3. При каких натуральных n число а =2ⁿ + 1 делится на 3?

Задание 4. Найти все делители числа 496 и сумму его собственных делителей.

Задание 5. Доказать, что если p > 4 и взаимно просто с 6, то p² – 1 делится на 24.

Задание 6. Найти НОД (1176, 315).

Задание 7. Решить систему сравнений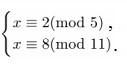



Задание 8. Решить систему сравнений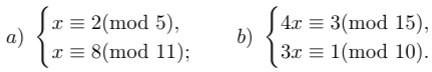



Задание 9. Решить систему сравнений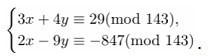



Задание 10. Найти остаток от деления:



Задание 10. Докажите, что число вида 5m + 2 (при целом m) не является полным квадратом.

ПРАКТИЧЕСКАЯ РАБОТА № 4 Применение классических шифров замены

Цель: научиться применять классические шифры замены.

Теоретические вопросы 1. Понятие криптографии.

2. 
   Понятие шифра.
   
3. 
   Шифр замены.
   
4. 
   Шифр многоалфавитной замены.
   
5. 
   Сходства и различия шифра Гронсфельда и шифра Цезаря.
   
6. 
   Биграммный шифр замены.
   

Задание 1. Выбрать один из методов замены: а) шифр Атбаш; б) шифр

Цезаря;

в) шифр Полибианский квадрат; г) шифр

Трисимуса;

д) шифр многоалфавитной замены Вижинера; е) шифр биграммами; ж) шифр Гронсфельда.

Составить алгоритм программы шифрования по выбранному методу.

Задание 2. Составить программу шифрования по выбранному методу.

Задание 3. Составить алгоритм программы расшифрования по выбранному методу.

Составить программу расшифрования по выбранному методу.

Задание 4. Расшифровать текст,

а) зашифрованный шифром Цезаря со сдвигом на 4 позиции:

Уокдгнбэылмбаноюзыбожмдлокндне

биь б) зашифрованный шифром Цезаря со сдвигом на 6 позиции:

Иыфщлзвмелнмцйкяиыкъбиьъзвгйякялмъзиьдъвбъ

жязъ в) зашифрованный заменой по кодовому слову «пароль»: випигьпжоймгсзпчгумйрпигяиьлйжбийржгясыипипльбийнсынгнсьзъ

ПРАКТИЧЕСКАЯ РАБОТА № 5

Применение классических шифров перестановки

Цель: научиться применять классические шифры перестановки.

Теоретические вопросы 1. Понятие криптографии.

2. 
   Понятие шифра.
   
3. 
   Шифр перестановки.
   
4. 
   Модификации шифров перестановки по таблице.
   
5. 
   Понятие «магический квадрат».
   
6. 
   Особенность шифра решетками.
   

Задание 1. Выбрать один из методов перестановки: а) обратное написание текста;

б) простая перестановка по таблице;

в) одиночная перестановка по ключу по таблице;

г) одиночная перестановка символов с пропусками по таблице;

д) двойные перестановки столбцов и строк;

е) шифр «Магический квадрат»;

ж) шифр «Решетки» или «Трафареты».

Составить алгоритм программы шифрования по выбранному методу.

Задание 2. Составить программу шифрования по выбранному методу.

Задание 3. Составить алгоритм программы расшифрования по выбранному методу.

Составить программу расшифрования по выбранному методу.

Задание 4. Дешифровать сообщения:

а) Бирои имч еыеес витсч арзки танет есарл лпюсп мотоо еипнф кйаои крслт мн;

б) тиооско нцрпоед иявдттж афэелиа ткокнбв еапанъг уитриоб;

в) икинорткелэоидаржделлок.

ПРАКТИЧЕСКАЯ РАБОТА № 6 Применение метода гаммирования

Цель: научиться применять метод гаммирования.

Теоретические вопросы

1. 
   Гаммирование: основные определения.
   
2. 
   Алгоритм шифрования текста методом гаммирования.
   
3. 
   Двоичное гаммирование: основные особенности.
   

Задание 1. Выбрать один из способов гаммирования: а) гаммирование по модулю К;

б) двоичное гаммирование.

Составить алгоритм программы шифрования по выбранному методу.

Задание 2. Составить программу шифрования по выбранному методу.

Задание 3. Составить алгоритм программы расшифрования по выбранному методу.

Составить программу расшифрования по выбранному методу.

ПРАКТИЧЕСКАЯ РАБОТА № 7

Криптоанализ шифра простой замены методом анализа частотности символов

Цель: научиться выполнять криптоанализ шифра простой замены методом анализа частотности символов.

Теоретические вопросы

1. 
   Понятие криптоанализа.
   
2. 
   Методика криптоанализа, основанная на исследовании частотности закрытого текста.
   
3. 
   Правило А. Керхоффа.
   

Задание 1. Получить от преподавателя текстовый файл, содержащий большой художественный текст на русском языке в открытом виде. Написать программу «Частота символов». Исследовать частотность символов открытого теста.

Задание 2. Получить от преподавателя текстовый файл, содержащий большой объем зашифрованного текста на русском языке. Исследовать частотность зашифрованного текста.

Задание 3. Сравнивая реальную частотность символов русского языка, полученную в пункте 1, с частотностями зашифрованного текста, составить таблицу замен алгоритма шифрования и расшифровать зашифрованный текст, реализовав программу дешифровки. Дешифровке подвергните только первые 15–20 символов, наиболее часто встречающиеся в шифротексте.

Задание 4. Выполнить эвристический анализ текста, полученного в результате дешифровки. По смыслу текста выявить те замены, которые оказались неверными, и сформировать верные замены. Доведите результат дешифровки до приемлемого (удобочитаемого) вида.

ПРАКТИЧЕСКАЯ РАБОТА № 8

Криптоанализ классических шифров методом полного перебора ключей

Цели: научиться выполнять криптоанализ классических шифров методом полного перебора ключей.

Теоретические вопросы

1. 
   Понятие криптоанализа.
   
2. 
   Понятие стойкости криптографического алгоритма.
   
3. 
   Типовые методы криптоанализа классических алгоритмов.
   
4. 
   Инструменты криптоанализа
   

Задание 1. Расшифровать фразу, зашифрованную столбцовой перестановкой: a) ОКЕСНВРП_ЫРЕАДЕЫН_В_РСИКО;

2. 
   ДСЛИЕЗТЕА_Ь_ЛЬЮВМИ_ _АОЧХК;
   
3. 
   НМВИАИ_НЕВЕ_СМСТУОРДИАНКМ;
   
4. 
   ЕДСЗЬНДЕ_МУБД_УЭ_КРЗЕМНАЫ;
   
5. 
   СОНРЧОУО_ХДТ_ИЕИ_ВЗКАТРРИ.
   

Задание 2. Расшифровать фразу, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки):

1. 
   СЯСЕ_ _ЛУНЫИАККННОГЯДУЧАТН;
   
2. 
   МСЕЫ_ЛЫВЕНТОСАНТУЕИ_РЛПОБ;
   
3. 
   АМНРИД_УЕБСЫ_ЕЙРСООКОТНВ_;
   
4. 
   ОПЧУЛС_БООНЕВ_ОЖАЕОНЕЩЕИН;
   
5. 
   ЕШИАНИРЛПГЕЧАВРВ_СЕЫНА_ЛО.
   

Задание 3. Расшифровать текст. Каждой букве алфавита соответствует двузначное число:

1) 39 25 20 34 82 63 66 46 35 20 25 82 86 39 51 74 35 51 66 20 44 37 25 27

51 35 44 20 90 37 51 25 25 51 63 91 20 11 37 46 48 25 20 37 61 51 14 82 82 66 82

35 29 82 91 25 51 74 51 24 78 51 24 59 46 86 51 44 74 20 25 37 37, 37 44 82 31 11

37 82 51 46 25 51 34 82 25 37 82 86 37 25 27 51 35 44 20 90 37 51 25 25 48 44

46 82 78 25 51 14 51 18 37 59 44, 51 74 82 35 20 90 37 59 44 66 90 82 25 25 48 44

37 61 10 44 20 18 20 44 37, 86 61 20 25 86 51 39 66 86 51 44 10 66 82 86 46 51

35 10 37 66 51 46 51 39 51 63 66 39 59 91 37. 56 46 51 86 20 66 20 82 46 66

59 24 35 10 18 37 78 51 35 18 20 25 37 91 20 90 37 63, 4651, 66 51 18 14 20 66

25 51 35 82 91 10 14 29 46 20 46 20 44 35 20 91 14 37 56 25 48 78 37 66 66 14 82

24. 
    51 39 20 25 37 63, 35 10 86 51 39 51 24 37 46 82 14 37 44 25 51 18 37 78 37 91
    
25. 
    37 78 91 25 20 31 46 51 61 51 66 25 51 39 25 48 78 39 37 24 20 78 10 18
    

35 51 91, 25 51 25 82 10 24 82 14 59 31 46 24 51 14 42 25 51 18 51 39 25 37

44 20 25 37 59 24 20 25 25 48 44 39 51 74 35 51 66 20 44, 66 56 37 46 20 59,

56 46 51 51 61 82 66 74 82 56 82 25 37 82 37 25 27 51 35 44 20 90 37 51 25 25 51 63

61 82 91 51 74 20 66 25 51 66 46 37 25 82 37 44 82 82 46 66 44 48 66 14 20, 82

66 14 37 51 46 66 10 46 66 46 39 10 82 46 39 37 24 37 44 20 59 10 18 35 51 91 20;

2) 74 29 23 27 17 99 71 25 49 32 29 34 27 63 32 25 17 99 60 62 25 34 95 29 53

59 82 27 71 29 77 99 34 27 91 17 99 71 49 99 27 15 60 32 25 50 27 17 62 27 95 27

50 25 91 32 59 77 95 29 50 25 99 59, 25 99 74 29 53 25 59 17 99 25 91 23 49 71 25

17 99 60 49 25 34 32 25 71 95 27 82 27 32 32 25 29 50 17 25 15 77 99 32 59 77

62 95 25 53 95 29 23 32 25 17 99 60 34 15 35 17 27 99 27 71 25 12 25 99 95 29 45

49 74 29. 62 95 27 63 34 27 71 17 27 12 25, 50 27 17 62 27 95 27 50 25 91 32 29

35 95 29 50 25 99 29 17 29 82 49 83 62 25 17 27 50 27 62 95 25 34 59 74 99 25

71 50 27 53 25 62 29 17 32 25 17 99 49 17 71 35 53 29 32 29 17 32 29 15 49 23

49 27 82 32 29 34 27 63 32 25 95 29 50 25 99 29 77 10 27 12 25 25 50 25 95 59 34

25 71 29 32 49 35 49 95 27 53 27 95 71 49 95 25 71 29 32 49 27 82 74 95 49 99 49 23

32 89 83 74 25 99 74 29 53 59 50 15 25 74 25 71 62 49 99 29 32 49 35 49 53

29 62 25 82 49 32 29 77 10 49 83 59 17 99 95 25 91 17 99 71. 34 15 35 62 25 17 15

27 34 32 49 83 25 62 99 49 82 29 15 60 32 25 62 95 49 82 27 32 27 32 49 27 34 49

17 74 25 71 89 83 82 29 17 17 49 71 25 71 12 25 95 35 23 27 91 53 29 82 27 32 89.

74 29 23 27 17 99 71 25 49 32 29 34 27 63 32 25 17 99 60 95 29 50 25 99 89 34

25 17 99 49 12 29 27 99 17 35 25 62 99 49 82 49 53 29 67 49 27 91 62 95 25 12 95 29

82 82 32 25 12 25 25 50 27 17 62 27 23 27 32 49 35.

ПРАКТИЧЕСКАЯ РАБОТА № 9 Криптоанализ шифра Вижинера

Цель: научиться выполнять криптоанализ шифра Виженера.

Теоретические вопросы 1. Понятие криптоанализа.

2. Шифр Виженера.

Задание 1. Составить алгоритм шифрования и расшифрования методом Виженера.

Задание 2. Задан некоторый текст зашифрованный шифром Виженера, требуется определить ключевое слово и прочитать открытый текст.

Шифрованный текст

Влцдутжбюцхъяррмшбрхцэооэцгбрьцмйфктъъюьмшэсяцпунуящэйтаьэдкцибр ьцгбрпачкъуцпъбьсэгкцъгуущарцёэвърюуоюэкааэбрняфукабъарпяъафкъиьжяффнйо яфывбнэнфуюгбрьсшьжэтбэёчюъюръегофкбьчябашвёэуъъюаднчжчужцёэвлрнчулб юпцуруньъшсэюъзкцхъяррнрювяспэмасчкпэужьжыатуфуярюравртубурьпэщлафоуф бюацмнубсюкйтаьэдйюнооэгюожбгкбрънцэпотчмёодзцвбцшщвщепчдчдръюьскасэг ъппэгюкдойрсрэвоопчщшоказръббнэугнялёкьсрбёуыэбдэулбюасшоуэтъшкрсдугэфл бубуъчнчтртпэгюкиугюэмэгюккъъпэгяапуфуэзьрадзьжчюрмфцхраююанчёчюъыхьъ цомэфъцпоирькнщпэтэузуябащущбаыэйчдфрпэцъьрьцъцпоилуфэдцойэдятррачкубу фнйтаьэдкцкрннцюабугюуубурьпйюэъжтгюркующоъуфъэгясуоичщщчдцсфырэдщэ ъуяфшёчцюйрщвяхвмкршрпгюопэуцчйтаьэдкцибрьцыяжтюрбуэтэбдуящэубъибрюв ъежагибрбагбрымпуноцшяжцечкфодщоъчжшйуъцхчщвуэбдлдъэгясуахзцэбдэулькнъ щбжяцэьрёдъьвювлрнуяфуоухфекьгцчччгэъжтанопчынажпачкъуъмэнкйрэфщэъьбуд эндадъярьеюэлэтчоубъцэфэвлнёэгфдсэвэёкбсчоукгаутэыпуббцчкпэгючсаъбэнэфърк ацхёваетуфяепьрювържадфёжбьфутощоявьъгупчршуитеачйчирамчюфчоуяюонкяжы кгсцбрясшчйотъъжрсщчл

ПРАКТИЧЕСКАЯ РАБОТА № 10 Применение методов генерации ПСЧ

Цель: изучение способов применения методов генерации ПСЧ.

Теоретические вопросы

1. 
   Псевдослучайные числа.
   
2. 
   Генератор псевдослучайных чисел.
   
3. 
   Свойства генератора псевдослучайных чисел для использования в криптографических целях.
   
4. 
   Принципы использования генераторов псевдослучайных чисел при потоковом шифровании.
   
5. 
   Методы генерации ПСЧ.
   

Задание 1. Написать программу, выполняющую задачу исследования ДСЧ для одного из следующих вариантов:

1. 
   Исследовать равномерность датчика (проверить гипотезу о равномерности распределения совокупности ДСЧ).
   
2. 
   Определить период ДСЧ для различных параметров.
   
3. 
   Исследовать автокорреляцию совокупности ДСЧ для различных параметров на глубину 100 отсчетов.
   
4. 
   Построить гистограмму частоты появления каждого возможного значения совокупности ДСЧ.
   

Задание 2. Разработать и отладить ПО для исследования датчика псевдослучайных чисел.

Представить результаты исследования в графическом виде.

ЛИТЕРАТУРА

Основная учебная литература:

Казарин О. В. Программно-аппаратные средства защиты информации. Защита программного обеспечения : учебник и практикум для среднего профессионального образования / О. В. Казарин, А. С. Забабурин. — Москва : Издательство Юрайт, 2021. — 312 с. — (Профессиональное образование). — ISBN 978-5-534-13221-2. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/476997

Дополнительная учебная литература:

Сети и телекоммуникации : учебник и практикум для среднего профессионального образования / К. Е. Самуйлов [и др.] ; под редакцией К. Е. Самуйлова, И. А. Шалимова, Д. С. Кулябова. — Москва : Издательство Юрайт, 2021. — 363 с. — (Профессиональное образование). — ISBN 978-5-9916-0480-2. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/475704