Главная страница
Навигация по странице:

  • Интервал содержаний % Середина интервала Частота n

  • Накопленная частость w

    		•

    мат методы. Практическая работа 1 Вариационный анализ Вариант 11 Задание


    Скачать 19.88 Kb.
    НазваниеПрактическая работа 1 Вариационный анализ Вариант 11 Задание
    Анкормат методы
    Дата26.04.2022
    Размер19.88 Kb.
    Формат файлаdocx
    Имя файла1.docx
    ТипПрактическая работа
    #498474

    Практическая работа №1

    Вариационный анализ

    Вариант 11

    Задание:

    • Рассчитать ряд распределения проб по содержанию в них Ni. Построить таблицу интервального вариационного ряда (для нормального распределения);

    • Построить графики: полигон, гистограмма, кумулята;

    • Рассчитать статистические характеристики: среднее значение (Ū), дисперсия(S2), стандарт(S), показатель асимметрии(A), эксцесс(E), коэффициент вариации(V);

    • Рассчитать по формулам значения моды(Mo), медианы(Med). По кумуляте определить медианное значение и сравнить его с вычисленным по формуле;

    • Вычислить критерий Пирсона(Х2) и выбрать наиболее подходящую вероятностную модель распределения;

    • Сделать вывод о характере вариационного ряда (по статистическим характеристикам, по степени изменчивости, по вероятностной модели распределения).

    Ход работы:

    Для упорядочения содержаний Ni в виде интервального вариационного ряда производим расчёт шага интервала содержаний по формуле Стерджесса(1):

    H = (Umax-Umin)/(1+3.32*lgN) (1);

    H – шаг, N – объем выборки, Umax- максимальное значение выборки, Umin – минимальное значение выборки.

    H = (10,7-0,1)/(1+3.32*lgN);

    По формуле (1) H = 1,8;

    Исключая экстремальные значения проб (1 значение, равное 33,6), объем выборки равен 31(n).

    По представленным данным постоим таблицу 1.

    Таблица 1. Интервальный вариационный ряд распределения проб по содержанию Ni

    Интервал содержаний %
    Середина интервала
    Частота

    ni
    Частость

    wi
    Накопленная частота

    nsi
    Накопленная частость

    wsi

    0,1 – 1,9
    1
    22
    0,71
    22
    0,71

    1,9 – 3,7
    2,8
    4
    0,13
    26
    0,84

    3,7 – 5,5
    4,6
    2
    0,06
    28
    0,9

    5,5 – 7,3
    6,4
    1
    0,033
    29
    0,933

    7,3 – 9,1
    8,2
    1
    0,033
    30
    0,966

    9,1 – 10,9
    10
    1
    0,033
    31
    1


    Вывод: По данным таблицы 1 в выборке содержание проб варьирует в интервале от 0,1% до 10,9%. При этом преобладают пробы с минимальными содержаниями в интервале от 0,15-1,9% . Пробы с содержаниями от 5,5% до 10,9% содержатся в выборке в минимальном количестве.

    Графически, данные представлены в виде кумуляты (приложение 1).

    Далее в программе «Статистика» производим расчет статистических характеристик (таблица 2).

    Таблица 2. Статистические характеристики
    N набл
    Среднее
    Минимум
    Максим.
    Дисперсия
    Ст.откл.
    Асимметрия
    Эксцесс

    Ni
    32,0
    1,3
    0,1
    5,9
    1,4
    1,2
    2,5
    7,3

    По данным таблицы 2, параметр асимметрии больше нуля, следовательно, преобладают пробы с минимальными значениями. Эксцесс также больше нуля, следовательно, вариационная кривая островершинная.

    Коэффициент вариации рассчитывается по формул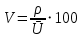е:

    , где

    ρ – стационарное отклонение;

    V – коэффициент вариации;

    Ū - среднее значение.

    V = 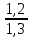*100;

    V = 92,3.

    По вычисленному значению коэффициента вариации можно сделать вывод о том, что характер распределения неравномерный (находится в интервале от 40 до 100).

    Далее выполняем расчет моды и медианы.

    Мода высчитывается по формуле:

    Mo = 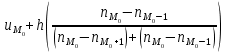, где

    UMo – начало модального интервала;

    h – шаг интервала;

    nMо – частота модального интервала;

    nMо-1 – частота интервала, предшествующего модальному;

    nMо+1 – частота интервала после модального интервала.

    Mo = 0,1 + 1,8(22/((22-4)(22-0)) = 1,09

    Медиана высчитывается по формуле:

    Med = 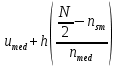, где

    Umed – начало медианного интервала;

    N - объём выборки (количество проб);

    nsm - накопленная частота интервала, предшествующего предыдущему;

    nmed - частота медианного интервала.

    Med = 0,1 + 1,8((32/2)/22) = 1,37

    Сравнивая значения моды и медианны, полученными по формулам со значениями, полученными по графикам, можно заметить, что значения, приблизительно, оказались равны. Медиана, найденная по графику кумуляты, равна 1,30. Мода, найденная по графикам полигона и гистограммы, равна 1

    Для выбора теоретической модели распределения производим, растёт распределения Пирсона. Проверяем нормальное распределение. Для этого вычисляем Х2 для нормального закона. Х2 при нормальном распределении не вычислен.

    Проверяем логнормальное распределение. Для этого вычисляем Х2. Хи-квадрат = 1,19486. Сравниваем с табличным. X2 табличный равен 18,307. Рассчитанный меньше табличного, следовательно, принимаем эту модель. Данная модель распределения будет наиболее подходящей, что подтверждают статистические характеристики (А > 0), а также вид гистограммы.

    написать администратору сайта