Вычерчивание контура детали с построением сопряжений. практическая 1. Практическая работа 1 Вычерчивание контура детали с построением сопряжений Г. Куйбышев 2021 г. Практическая работа 1
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
ГБПОУ НСО «Куйбышевский политехнический колледж» ОП. 01 Инженерная графика Практическая работа № 1 «Вычерчивание контура детали с построением сопряжений» Г. Куйбышев 2021 г. Практическая работа №1 Цель: Закрепить умения построения сопряжений. Образовательные результаты, заявленные во ФГОС: Обучающийся должен уметь: - оформлять технологическую и конструкторскую документацию в соответствии с действующей нормативно-технической документацией; - читать чертежи, технологические схемы, спецификации и технологическую документацию по профилю специальности; знать: - законы, методы и приемы проекционного черчения; - правила оформления и чтения конструкторской и технологической документации; Задачи практической работы: Вычертить изображения контуров деталей, указанных на рисунке задания, нанести размеры. Задание выполнить на листе чертежной бумаги формата А4. Варианты задания представлены в таблице 1. Обеспеченность занятия: - посадочные места по количеству обучающихся; - рабочее место преподавателя; - мультимедиа-проектор; - экран. - бумага для черчения ф.А4 - карандаш чернографитный твердость М, Т; - ластик; - циркуль; - точилка для карандашей; - линейка -практическая работа № 1 в электронном и бумажном варианте. Сопряжением называется плавный переход одной линии в другую. Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях: 1 Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения (рисунок 2 а). 2 Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения (рисунок 2 б). 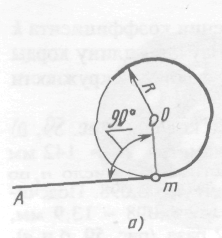 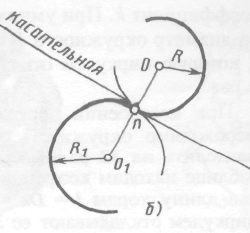 Рисунок 2 – Положения о сопряжениях а – для прямой и дуги; б – для двух дуг Сопряжение двух сторон угла дугой окружности и заданного радиуса Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса выполняют следующим образом: Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии (рисунок 3 а, б). Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n1, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла. При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рисунок 3 в). Из вершины угла А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n1. Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения. 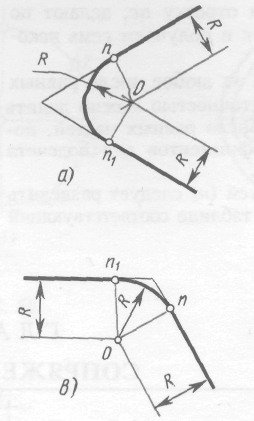  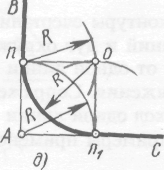 Рисунок 3 – Сопряжения углов а – острого; б – тупого; в – прямого Сопряжение прямой с дугой окружности Сопряжение прямой с дугой окружности может быть выполнено с помощью дуги с внутренним касанием (рисунок 4 б) и дуги с внешним касанием (рисунок 4 а). Для построения сопряжения внешним касанием проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, равном радиусу r(радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой ab в точке О1. Точка О1 является центром дуги сопряжения. Точку сопряжения с находят на пересечении прямой ОО1 с дугой окружности радиуса R. Точка сопряжения С1является основанием перпендикуляра, опущенного из центра О1 на данную прямую АВ. С помощью аналогичных построений могут быть найдены точки О2, С2, С3. На рисунке 6 б выполнено сопряжение дуги радиуса R с прямой АВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О1 находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из центра О радиусом, равным разности R-r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О1 на данную прямую. Точку сопряжения с находят на пересечении прямой ОО1 с сопрягаемой дугой. 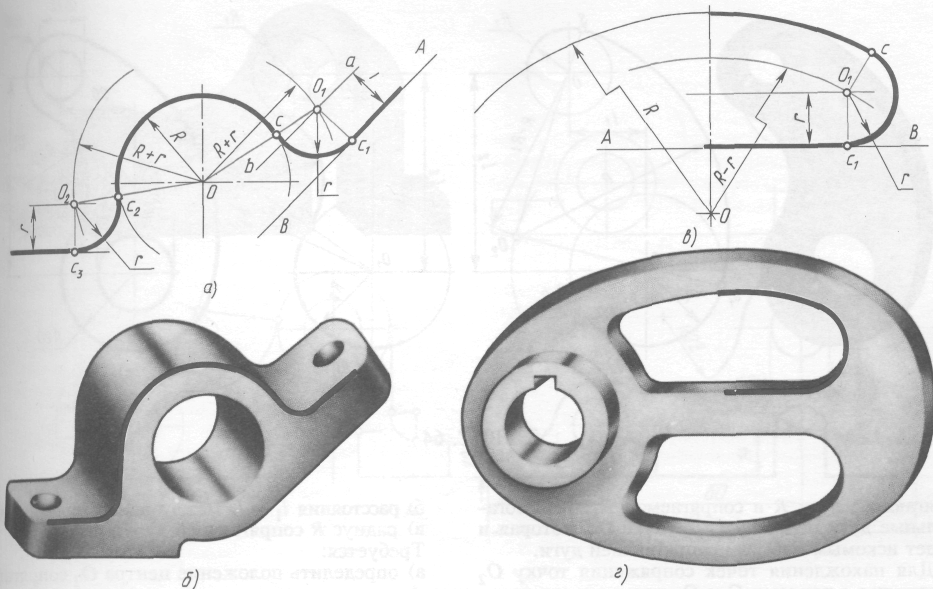 Рисунок 4 – Сопряжение дуги с прямой а – с внешним касанием; б – с внутренним касанием Сопряжение дуги с дугой Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным. При внутреннем сопряжении центры О и О1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рисунок 5 а). 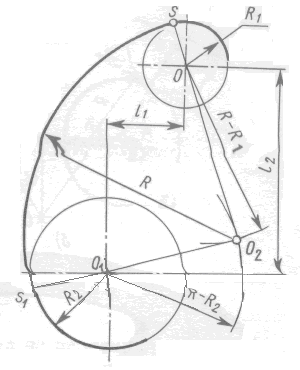 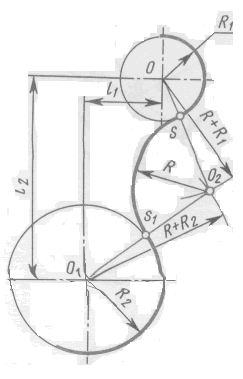 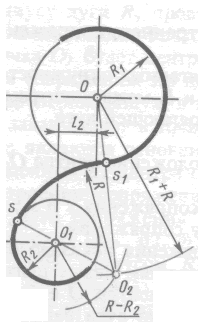 Рисунок 5 – Сопряжения дуг а – внутреннее; б – внешнее; в – смешанное. При внешнем сопряжении сопрягаемых дуг радиусов R1 иR2 находятся вне сопрягающей дуги радиуса R (рисунок 5 б). При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиусаR, а центр О другой сопрягаемой дуги вне ее (рисунок 5 в). При вычерчивании контуров сложных деталей важно уметь распознавать в плавных переходах те или иные виды сопряжений и уметь их вычерчивать. Для приобретения навыков в построении сопряжений выполняют упражнения по вычерчиванию контуров сложных деталей. Для этого необходимо определить порядок построения сопряжений и только после этого приступать к их выполнению. Таблица 1 – Варианты задания 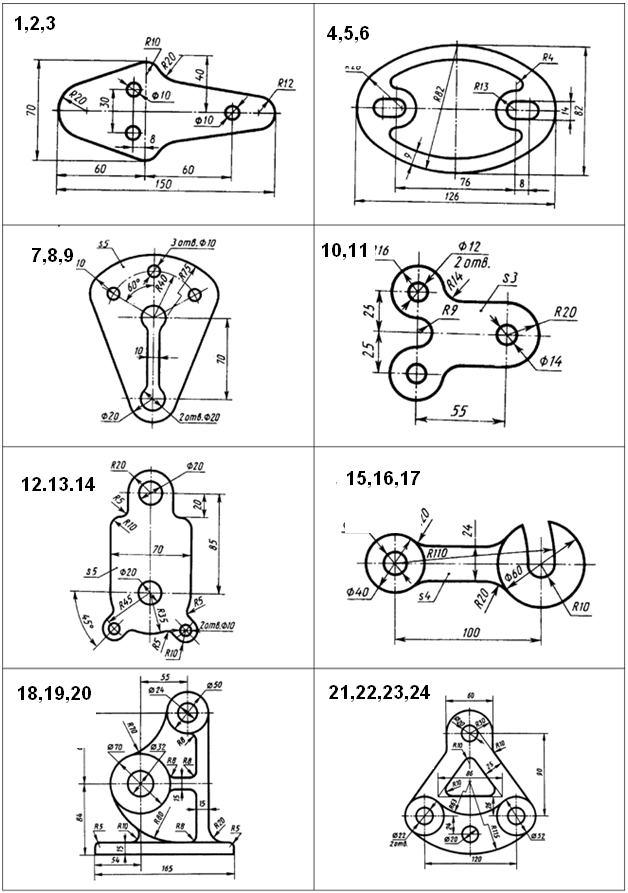 УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ При выполнении каждой задачи должна соблюдаться определенная последовательность геометрических построений: – осевые, центровые линии, основные начертательные; – дуги, закругления; – обводка, штриховка, выносные линии; – размеры. Критерии оценки Если чертеж выполнен, верно, аккуратно – оценка ставится в соответствии с выбранным вариантом Если чертеж выполнен, верно, есть незначительные помарки и замечания преподавателя – оценка на бал ниже Если чертеж содержит более пяти грубых ошибок - неудовлетворительно. |
