ЦК. Практическая работа 2 ЦК. Практическая работа 2 Методы тестирования в ходе выполнения практической работы необходимо разработать алгоритм решения задачи
 Скачать 273.36 Kb. Скачать 273.36 Kb.
|
|
Практическая работа № 2 – Методы тестирования В ходе выполнения практической работы необходимо: разработать алгоритм решения задачи; реализовать индивидуальный вариант задания на любом известном студенту языке программирования. Внести в программу несколько ошибок. выполнить тестирование методами белого и черного ящика; результаты тестирования представить в виде таблиц; оформить отчет по лабораторной работе, включающий разделы: постановка задачи, блок-схема алгоритма решения задачи, тестовые варианты и результаты тестирования, скриншоты работы программы, код программы, выводы о достоинствах и недостатках каждой стратегии. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Тестирование программного обеспечения включает в себя целый комплекс действий, аналогичных последовательности процессов разработки программного обеспечения. В него входят: постановка задачи для теста; проектирование теста; написание тестов; тестирование тестов; выполнение тестов; изучение результатов тестирования. Наиболее важным является проектирование тестов. Существуют разные подходы к проектированию тестов. Первый состоит в том, что тесты проектируются на основе внешних спецификаций программ и модулей либо спецификаций сопряжения модуля с другими модулями, программа при этом рассматривается как «черный ящик». Смысл теста заключается в том, чтобы проверить, соответствует ли программа внешним спецификациям. При этом содержание модуля не имеет значения. Такой подход получил название — стратегия «черного ящика». Второй подход — стратегия «белого ящика», основан на анализе логики программы. При таком подходе тестирование заключается в проверке каждого пути, каждой ветви алгоритма. При этом внешняя спецификация во внимание не принимается. Ни один из этих подходов не является оптимальным. Реализация тестирования методом «черного ящика» сводится к проверке всех возможных комбинаций входных данных. Невозможно протестировать программу, подавая на вход бесконечное множество значений, поэтому ограничиваются определенным набором данных. При этом исходят из максимальной отдачи теста по сравнению с затратами на его создание. Она измеряется вероятностью того, что тест выявит ошибки, если они имеются в программе. Затраты измеряются временем и стоимостью подготовки, выполнения и проверки результатов теста. Тестирование методом «белого ящика» также не дает 100%-ной гарантии того, что модуль не содержит ошибок. Даже если предположить, что выполнены тесты для всех ветвей алгоритма, нельзя с полной уверенностью утверждать, что программа соответствует ее спецификациям. Например, если требовалось написать программу для вычисления кубического корня, а программа фактически вычисляет корень квадратный, то реализация будет совершенно неправильной, даже если проверить все пути. Вторая проблема — отсутствующие пути. Если программа реализует спецификации не полностью (например, отсутствует такая специализированная функция, как проверка на отрицательное значение входных данных программы вычисления квадратного корня), никакое тестирование существующих путей не выявит такой ошибки. И наконец, проблема зависимости результатов тестирования от входных данных. Одни данные будут давать правильные результаты, а другие нет. Таким образом, полное тестирование программы невозможно, т. е. никакое тестирование не гарантирует полное отсутствие ошибок в программе. Поэтому необходимо проектировать тесты таким образом, чтобы увеличить вероятность обнаружения ошибки в программе. СТРАТЕГИЯ «БЕЛОГО ЯЩИКА» Существуют следующие методы тестирования по принципу «белого ящика»: покрытие операторов; покрытие решений; покрытие условий; покрытие решений/условий; комбинаторное покрытие условий. Метод покрытия операторов Целью этого метода тестирования является выполнение каждого оператора программы хотя бы один раз. Тестовый пример
Если для тестирования задать значения переменных А = 2, В = 0, Х = 3, будет реализован путь асе, т. е. каждый оператор программы выполнится один раз (рис. 1, а). Но если внести в алгоритм ошибки — заменить в первом условии and на or, а во втором Х > 1 на Х < 1 (рис. 1, б), ни одна ошибка не будет обнаружена (табл. 1). Кроме того, путь abd вообще не будет охвачен тестом, и, если в нем есть ошибка, она также не будет обнаружена. В таблице 1 ожидаемый результат определяется по блок-схеме на рис. 1 а), а фактический — по рис. 1 б). Как видно из этой таблицы, ни одна из внесенных в алгоритм ошибок не будет обнаружена.
Таблица 1 – результат тестирования методом покрытия операторов
Метод покрытия решений (покрытия переходов) Согласно методу покрытия решений каждое направление перехода должно быть реализовано, по крайней мере, один раз. Этот метод включает в себя критерий покрытия операторов, так как при выполнении всех направлений переходов выполнятся все операторы, находящиеся на этих направлениях. Для программы из тестового примера покрытие решений может быть выполнено двумя тестами, покрывающими пути {ace, abd}, либо {aсd,abe}. Для этого выберем следующие исходные данные; {А = 3, В = 0, Х = 3} — в первом случае и {А = 2, В = 1, Х = 1} — во втором. Однако путь, где X не меняется, будет проверен с вероятностью 50 %: если во втором условии вместо условия Х> 1 записано Х < 1, то ошибка не будет обнаружена двумя тестами (табл. 2). Таблица 2 – результат тестирования методом покрытия решений
Метод покрытия условий Этот метод может дать лучшие результаты по сравнению с предыдущими. В соответствии с методом покрытия условий записывается число тестов, достаточное для того, чтобы все возможные результаты каждого условия в решении выполнялись, по крайней мере, один раз. В нашем тестовом примере имеем четыре условия: {А> 1, B = 0}, {А = 2, Х> 1}. Следовательно, требуется достаточное число тестов, такое, чтобы реализовать ситуации, где А > 1, А < 1, В = 0 и В <> 0 в точке а и А = 2, А <> 2, Х> 1 и Х< 1 в точке b. Тесты, удовлетворяющие критерию покрытия условий (табл. 3), и соответствующие им пути: а) А = 2, B = 0, Х = 4 асе; 6) А = 1, В = 1, Х = 0 abd. Таблица 3 – результаты тестирования методом покрытия условий
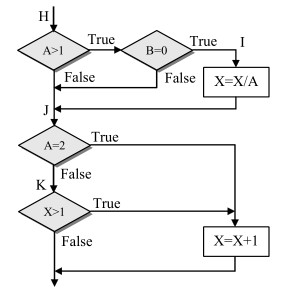
Критерий покрытия решений (условий) Критерий покрытия решений/условий требует такого достаточного набора тестов, чтобы все возможные результаты каждого условия в решении выполнялись по крайней мере один раз, все результаты каждого решения выполнялись по крайней мере один раз и, кроме того, каждой точке входа передавалось управление по крайней мере один раз. Тесты A=2, B=0, X=4 ace; A=1, B=1, X=0 abd. отвечают и критерию покрытия решений/условий. Это является следствием того, что одни условия приведенных решений скрывают другие условия в этих решениях. Так, если условие А>1 будет ложным, транслятор может не проверять условия В=0, поскольку при любом результате условия В=0, результат решения ((А>1)&(В=0)) примет значение ложь. Следовательно, недостатком критерия покрытия решений/ условий является невозможность его применения для выполнения всех результатов всех условий. Другая реализация рассматриваемого примера приведена на рисунке 2. Многоусловные решения исходной программы разбиты на отдельные решения и переходы. Наиболее полное покрытие тестами в этом случае выполняется так, чтобы выполнялись все возможные результаты каждого простого решения. Для этого нужно покрыть пути HILP (тест А=2, В=0, Х=4), HIMKT (тест А=3, В=1, Х=0), HJKT (тест А=0, В=0, Х=0), HJKR (тест А=0, В=0, Х=2).
Протестировав алгоритм на рисунке 2, нетрудно убедиться в том, что критерии покрытия условий и критерии покрытия решений/условий недостаточно чувствительны к ошибкам в логических выражениях. Метод комбинаторного покрытия условий Критерий комбинаторного покрытия условий удовлетворяет также и критериям покрытия решений, покрытия условий и покрытия решений/условий. Этот метод требует создания такого числа тестов, чтобы все возможные комбинации результатов условия в каждом решении выполнялись по крайней мере один раз. По этому критерию в рассматриваемом примере должны быть покрыты тестами следующие восемь комбинаций: A > 1, B = 0. A > 1, B <> 0. A < 1, B = 0. A < 1, B <> 0. А = 2, Х > 1. А = 2, Х < 1. А <> 2, Х > 1. A <> 2, X < 1. Для того чтобы протестировать эти комбинации, необязательно использовать все 8 тестов. Фактически они могут быть покрыты четырьмя тестами (табл. 4): А = 2, B = 0, Х = 4 {покрывает 1, 5}; А = 2, B = 1, Х = 1 {покрывает 2, 6}; А = 0.5, B = 0, Х = 2 {покрывает 3, 7}; A = 1, B = 0, Х = 1 {покрывает 4, 8}. Таблица 4 – результаты тестирования методом комбинаторного покрытия условий
Таким образом, для программ, содержащих только одно условие на каждое решение, минимальным является критерий, набор тестов которого: вызывает выполнение всех результатов каждого решения, по крайней мере, один раз; передает управление каждой точке входа (например, точке входа, case-единице) по крайней мере один раз (чтобы обеспечить выполнение каждого оператора программы по крайней мере один раз). Для программ, содержащих решения, каждое из которых имеет более одного условия, минимальный критерий состоит из набора тестов, вызывающих выполнение всех возможных комбинаций результатов условий в каждом решении и передающих управление каждой точке входа программы, по крайней мере, один раз. Тестирование методом белого ящика (индивидуальные задания) В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных после минимального элемента. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных между минимальным и максимальным элементами. В одномерном динамическом массиве, состоящем из n элементов, вычислить среднеарифметическое значение элементов массива. В одномерном динамическом массиве, состоящем из n элементов, вычислить среднеквадратическое значение элементов массива. В одномерном динамическом массиве, состоящем из n элементов, вычислить среднегеометрическое значение ненулевых элементов массива. В одномерном динамическом массиве, состоящем из n элементов, вычислить среднегармоническое значение положительных элементов массива. В одномерном динамическом массиве, состоящем из nэлементов, поменять местами максимальный и минимальный элементы. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных между первым и последним отрицательными элементами. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных до последнего положительного элемента. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных между первым и последним нулевыми элементами. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму модулей элементов массива, расположенных после первого элемента, равного нулю. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму положительных элементов массива, расположенных до максимального элемента. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных до минимального элемента. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных между первым и последним положительными элементами. В одномерном динамическом массиве, состоящем из n элементов, вычислить среднее значение элементов, расположенных в массиве между первым последним нулевыми элементами. В одномерном динамическом массиве, состоящем из n элементов, вычислить произведение элементов массива, расположенных между первым и вторым нулевыми элементами. В одномерном динамическом массиве, состоящем из n элементов, определить номер минимального и максимального элементов массива. В одномерном динамическом массиве, состоящем из n элементов, определить сумму модулей элементов массива, расположенных после первого отрицательного элемента. В одномерном динамическом массиве, состоящем из n элементов, определить количество элементов массива, больших С. В одномерном динамическом массиве, состоящем из n элементов, определить количество элементов массива, меньших С. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму отрицательных элементов массива. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму положительных элементов массива. В одномерном динамическом массиве, состоящем из n элементов, вычислить произведение элементов массива с четными номерами. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных после минимального элемента. В одномерном динамическом массиве, состоящем из n элементов, вычислить сумму элементов массива, расположенных до максимального элемента. СТРАТЕГИЯ «ЧЕРНОГО ЯЩИКА» Одним из способов проверки программ является стратегия тестирования, называемая стратегией "черного ящика" или тестированием с управлением по данным. В этом случае программа рассматривается как "черный ящик" и такое тестирование имеет целью выяснения обстоятельств, в которых поведение программы не соответствует спецификации. Для обнаружения всех ошибок в программе необходимо выполнить исчерпывающее тестирование, т.е. тестирование на всех возможных наборах данных. Для тех же программ, где исполнение команды зависит от предшествующих ей событий, необходимо проверить и все возможные последовательности. Очевидно, что построение исчерпывающего входного теста для большинства случаев невозможно. Поэтому, обычно выполняется "разумное" тестирование, при котором тестирование программы ограничивается прогонами на небольшом подмножестве всех возможных входных данных. Естественно при этом целесообразно выбрать наиболее подходящее подмножество (подмножество с наивысшей вероятностью обнаружения ошибок). Правильно выбранный тест подмножества должен обладать следующими свойствами: 1) уменьшать, причем более чем на единицу число других тестов, которые должны быть разработаны для достижения заранее определенной цели «приемлемого» тестирования: 2) покрывать значительную часть других возможных тестов, что в некоторой степени свидетельствует о наличии или отсутствии ошибок до и после применения этого ограниченного множества значений входных данных. Стратегия "черного ящика" включает в себя следующие методы формирования тестовых наборов: эквивалентное разбиение; анализ граничных значений; анализ причинно-следственных связей; предположение об ошибке. Эквивалентное разбиение Основу метода составляют два положения: 1.Исходные данные программы необходимо разбить на конечное число классов эквивалентности, так чтобы можно было предположить, что каждый тест, являющийся представителем некоторого класса, эквивалентен любому другому тесту этого класса. Иными словами, если тест какого-либо класса обнаруживает ошибку, то предполагается, что все другие тесты этого класса эквивалентности тоже обнаружат эту ошибку и наоборот. 2.Каждый тест должен включать по возможности максимальное количество различных входных условий, что позволяет минимизировать общее число необходимых тестов. Первое положение используется для разработки набора "интересных" условий, которые должны быть протестированы, а второе - для разработки минимального набора тестов. Разработка тестов методом эквивалентного разбиения осуществляется в два этапа: – выделение классов эквивалентности; – построение тестов. Выделение классов эквивалентности Классы эквивалентности выделяются путем выбора каждого входного условия (обычно это предложение или фраза из спецификации) и разбиением его на две или более групп. Для этого используется таблица следующего вида:
Выделение классов эквивалентности является эвристическим процессом, однако при этом существует ряд правил: Если входные условия описывают область значений; Если входное условие описывает число значений, то определяется один правильный класс эквивалентности и два неправильных; Если входное условие описывает множество входных значений и есть основания полагать, что каждое значение программист трактует особо, то определяется правильный класс эквивалентности для каждого значения и один неправильный класс; Если входное условие описывает ситуацию «должно быть, то определяется один правильный класс эквивалентности и один неправильный; Если есть любое основание считать, что различные элементы класса эквивалентности трактуются программой неодинаково, то данный класс разбивается на меньшие классы эквивалентности. Анализ граничных значений Граничные условия - это ситуации, возникающие на, выше или ниже границ входных классов эквивалентности. Анализ граничных значений отличается от эквивалентного разбиения следующим: Выбор любого элемента в классе эквивалентности в качестве представительного при анализе граничных условий осуществляется таким образом, чтобы проверить тестом каждую границу этого класса. При разработке тестов рассматриваются не только входные условия (пространство входов), но и пространство результатов. Применение метода анализа граничных условий требует определенной степени творчества и специализации в рассматриваемой проблеме. Тем не менее, существует несколько общих правил этого метода: Правило 1 - построить тесты для границ области и тесты с неправильными входными данными для ситуаций незначительного выхода за границы области, если входное условие описывает область значений (например, для области входных значений от -1.0 до +1.0 необходимо написать тесты для ситуаций -1.0, +1.0, -1.001 и +1.001). Правило 2 - построить тесты для минимального и максимального значений условий и тесты, большие и меньшие этих двух значений, если входное условие удовлетворяет дискретному ряду значений. Например, если входной файл может содержать от 1 до 255 записей, то проверить 0,1,255 и 256 записей. Использовать правило 1 для каждого выходного условия. Причем, важно проверить границы пространства результатов, поскольку не всегда границы входных областей представляют такой же набор условий, как и границы выходных областей. Не всегда также можно получить результат вне выходной области, но, тем не менее, стоит рассмотреть эту возможность. Использовать правило 2 для каждого выходного условия. Если вход или выход программы есть упорядоченное множество (например, последовательный файл, линейный список, таблица), то сосредоточить внимание на первом и последнем элементах этого множества. Попробовать свои силы в поиске других граничных условий. Анализ граничных условий, если он применен правильно, является одним из наиболее полезных методов проектирования тестов. Однако следует помнить, что граничные условия могут быть едва уловимы и определение их связано с большими трудностями, что является недостатком этого метода. Второй недостаток связан с тем, что метод анализа граничных условий не позволяет проверять различные сочетания исходных данных. Анализ причинно-следственных связей Метод анализа причинно-следственных связей помогает системно выбирать высокорезультативные тесты. Он дает полезный побочный эффект, позволяя обнаруживать неполноту и неоднозначность исходных спецификаций. Для использования метода необходимо понимание булевской логики (логических операторов - и, или, не). Построение тестов осуществляется в несколько этапов. 1. Спецификация разбивается на «рабочие» участки, так как таблицы причинно-следственных связей становятся громоздкими при применении метода к большим спецификациям. Например, при тестировании компилятора в качестве рабочего участка можно рассматривать отдельный оператор языка. 2. В спецификации определяются множество причин и множество следствий. Причина есть отдельное входное условие или класс эквивалентности входных условий. Следствие есть выходное условие или преобразование системы. Каждым причине и следствию приписывается отдельный номер. 3. На основе анализа семантического (смыслового) содержания спецификации строится таблица истинности, в которой последовательно перебираются все возможные комбинации причин и определяются следствия каждой комбинации причин. Таблица снабжается примечаниями, задающими ограничения и описывающими комбинации причин и/или следствий, которые являются невозможными из-за синтаксических или внешних ограничений. Аналогично, при необходимости строится таблица истинности для класса эквивалентности. Примечание. При этом можно использовать следующие приемы: По возможности выделять независимые группы причинно-следственных связей в отдельные таблицы. Истина обозначается "1". Ложь обозначается "0". Для обозначения безразличных состояний условий применять обозначение "Х", которое предполагает произвольное значение условия (0 или 1). 4. Каждая строка таблицы истинности преобразуется в тест. При этом по возможности следует совмещать тесты из независимых таблиц. Недостаток метода заключается в том, что он неадекватно исследует граничные условия. Предположение об ошибке Часто программист с большим опытом выискивает ошибки "без всяких методов". При этом он подсознательно использует метод "предположение об ошибке". Процедура метода предположения об ошибке в значительной степени основана на интуиции. Основная идея метода состоит в том, чтобы перечислить в некотором списке возможные ошибки или ситуации, в которых они могут появиться, а затем на основе этого списка составить тесты. Другими словами, требуется перечислить те специальные случаи, которые могут быть не учтены при проектировании. ПРИМЕР ПРИМЕНЕНИЯ МЕТОДОВ ТЕСТИРОВАНИЯ «ЧЕРНЫЙ ЯЩИК» Пусть необходимо выполнить тестирование программы, определяющей точку пересечения двух прямых на плоскости. Попутно, она должна определять параллельность прямой одной их осей координат. В основе программы лежит решение системы линейных уравнений: Ax + By = C и Dx + Ey = F. 1.1 Метод эквивалентных разбиений Используя метод эквивалентных разбиений, получаем для всех коэффициентов один правильный класс эквивалентности (коэффициент - вещественное число) и один неправильный (коэффициент - не вещественное число). Откуда можно предложить 7 тестов: 1) все коэффициенты - вещественные числа; 2) - 7) поочередно каждый из коэффициентов - не вещественное число. 1.2. Метод граничных условий Можно считать, что для исходных данных граничные условия отсутствуют (коэффициенты - "любые" вещественные числа). Для результатов - получаем, что возможны варианты: единственное решение, прямые сливаются (множество решений), прямые параллельны (отсутствие решений). Следовательно, можно предложить тесты, с результатами внутри области: результат - единственное решение ( 0); результат - множество решений ( = 0 и x=y=0); результат - отсутствие решений ( = 0, но x0 или y0); и с результатами на границе: = 0,01; = -0,01; = 0, x = 0,01, y = 0; = 0, y = -0,01, x = 0. 1.3. Метод анализа причинно-следственных связей Определяем множество условий. а) для определения типа прямой: 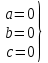 - для определения типа и существования первой прямой; - для определения типа и существования первой прямой;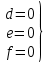 - для определения типа и существования второй прямой; - для определения типа и существования второй прямой;б) для определения точки пересечения: = 0 x = 0 y = 0 Выделяем три группы причинно-следственных связей (определение типа и существования первой линии, определение типа и существования второй линии, определение точки пересечения) и строим таблицы истинности.
Такая же таблица строится для второй прямой.
Каждая строка этих таблиц преобразуется в тест. При возможности (с учетом независимости групп) берутся данные, соответствующие строкам сразу двух или всех трех таблиц. В результате к уже имеющимся тестам добавляются: проверки всех случаев расположения обеих прямых - 6 тестов по первой прямой вкладываются в 6 тестов по второй прямой так, чтобы варианты не совпадали, - 6 тестов; выполняется отдельная проверка несовпадения условия x = 0 или y = 0 (в зависимости от того, какой тест был выбран по методу граничных условий) - тест также можно совместить с предыдущими 6 тестами; 1.4. Метод предположения об ошибке Добавим еще один тест: все коэффициенты - нули. Всего получили 20 тестов по всем четырем методикам. Если еще попробовать вложить независимые проверки, то возможно число тестов можно еще сократить (для каждого теста необходимо указать результат!). Тестирование методом черного ящика (индивидуальные задания) Разработать программу решения квадратного уравнения, где a, b, c - любые вещественные числа. Разработать программу определения суммарной длины тени, которую отбрасывают на ось ОХ отрезки, параллельные этой оси и заданные координатами x начала и конца отрезка. Разработать программу определения вида четырехугольника, заданного координатами вершин на плоскости: квадрат, прямоугольник, параллелограмм, ромб, равнобедренная трапеция, прямоугольная трапеция, трапеция общего вида, четырехугольник общего вида. Пользователь заполняет анкету и в одной из граф пишет свою дату рождения. Разработать программу, которая определяет знак зодиака пользователя по дате рождения. Пользователь вводит число. Разработать программу, которая определяет, что он ввел год, а также рассматривает и определяет тип года (високосный или нет). Разработать программу определения вида треугольника, заданного длинами его сторон: равносторонний, равнобедренный, прямоугольный, разносторонний. Программа считает сумму последовательности 15 целых чисел без максимального элемента последовательности. Программа из последовательности 15 целых чисел выводит предпоследнее максимальное значение элемента. Программа считает сумму последовательности 15 целых чисел без минимального элемента последовательности. Программа из последовательности 15 целых чисел выводит предпоследнее минимальное значение элемента. Программа из последовательности 15 целых чисел выводит минимальное значение элемента и предпоследний по величине элемент. Программа из последовательности 15 целых чисел выводит максимальное значение элемента и второй по величине элемент. Программа из последовательности 15 целых чисел выводит максимальное значение элемента, устанавливает, сколько раз это значение встречается. Программа из последовательности 15 целых чисел выводит максимальное значение элемента, минимальное значение элемента и их сумму. Программа осуществляет сортировку вставками массива из 10 элементов Программа осуществляет сортировку слиянием массива из 10 элементов Программа осуществляет пирамидальную сортировку массива из 10 элементов Программа должна находить точку пересечения двух линий. Даны следующие уравнения линий: y = ax^2 + bx + c и y = dx + k, где a, b, c, d, k — это числа, которые вводятся с клавиатуры. Необходимо найти значение икса. Есть координаты двух клеток шахматной доски. Вывести Yes, если слон может за один ход перейти с одной клетки в другую. В другом случае вывести No Разработать программу определения вида четырехугольника, заданного координатами вершин на плоскости: квадрат, прямоугольник, параллелограмм, ромб, равнобедренная трапеция, прямоугольная трапеция, трапеция общего вида, четырехугольник общего вида. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||