Практическая работа №2. Практическая работа 2 Определение сил реакций связей Цель работы научиться определять силы реакций связей. Содержание отчета
 Скачать 322.16 Kb. Скачать 322.16 Kb.
|
|
Практическая работа №2 Определение сил реакций связей Цель работы: научиться определять силы реакций связей. Содержание отчета: Номер практической работы. Название работы. Цель работы. Прочитать теоретическую часть. Записать в тетрадь методические указания по выполнению практической работы. Записать в тетрадь пример 1 (с рисунком и решением) Ответить на контрольные вопросы и задания. Теоретическая часть Тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным. Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, называется связью. Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или реакцией связи. Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей. Все виды связей можно разделить на несколько типов. Связь – гладкая опора (без трения). 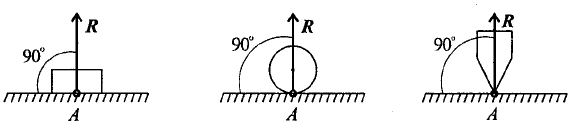 Рисунок 1.1 Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рисунок 1.1). Гибкая связь (нить, веревка, трос, цепь). Реакция нити направлена вдоль нить от тела, при этом нить может быть только растянута (рисунок 1.2). 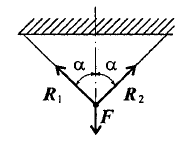 Рисунок 1.2 Жесткий стержень. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи (рисунок 1.3). 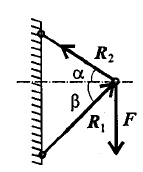 Рисунок 1.3 Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров. Подвижный шарнир. Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности (рисунок 1.4). 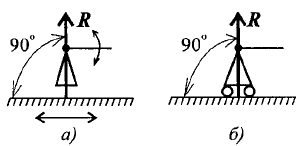 Рисунок 1.4 Неподвижный шарнир. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать в виде двух составляющих: горизонтальной и вертикальной (рисунок 1.5). 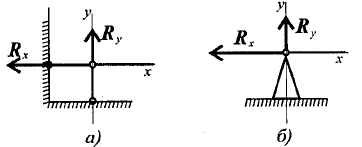 Рисунок 1.5 Защемление или «заделка». Любые перемещения точки крепления невозможны. Реактивную силу принято представлять в виде двух составляющих вдоль осей координат (рисунок 1.6). 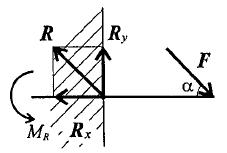 Рисунок 1.6 Методические указания по выполнению практической работы 1. Указывают точку, равновесие которой рассматривается. В задачах такой точкой является центр тяжести тела или точка пересечения всех стержней и нитей. 2. Прикладывают к рассматриваемой тачке активные силы. В задачах активными силами являются собственный вес тела или вес груза, которые направлены вниз (правильнее — к центру тяжести земли). Направление действия этой силы устанавливается из чертежа. Вас тела принято обозначать буквой G. 3. Мысленно отбрасывают связи, заменяя их действие реакциями связей. В предлагаемых задачах используются три вида связей — идеально гладкая плоскость, идеально жесткие прямолинейные стержни и идеально гибкие нити, — в дальнейшем именуемые соответственно плоскостью, стержнем и нитью. При замене связей их реакциями следует помнить, что реакция плоскости направлена по нормали (перпендикуляру) к ней в точке контакта (соприкосновения), а реакции стержня и нити — по их осям. К рассматриваемой точке прикладывают реакции связей. Лучше сделать это на отдельном чертеже, выполненном схематически, придерживаясь масштаба при изображении углов. В результате получают систему трех сходящихся сил. 4. Выбирают положение прямоугольной системы координат. Начало координат совмещают с точкой, равновесие которой рассматривается. Положение осей может быть выбрано произвольно и на конечном результате при правильном решении это не отражается. Обычно используют один из двух приемов для выбора направления осей координат. Первый: одну из осей направляют так, чтобы она совпадала с направлением одной из неизвестных реакций, а другая при этом состояла бы с первой угол 90º. Второй: ось y направляют вертикально, а ось x – горизонтально. Во всех случаях следует определить углы между реакциями и координатными осями и указать их на чертеже. 5. Составляют уравнения равновесия вида 1) Напомним, что проекцией силы на ось является произведение модуля (величины) этой силы на косинус угла между направлениями действия силы и оси. Если угол между направлениями силы и оси острый, т.е. направление оси и силы совпадает, то перед величиной проекции ставится знак «плюс», если тупой, т.е. сила и ось направлены в противоположные стороны – «минус». Если ответ получился со знаком «минус», то это означает, что направление реакции на чертеже было выбрано неверно. Такой ответ не является ошибкой решения. 6. Выполняют проверку решения. Обычно она делается графическим или другими способами, но может быть выполнена и аналитически. Для этого следует изменить положение осей координат и решить задачу в новой системе. Ответы должны быть одинаковыми. Пример 1. Определить величину и направление реакций связей для схемы, приведенной на рис. 1, а под действием груза G = 30 кН. Проверить правильность определения реакций. Решение. 1. В задаче рассматривается равновесие тела, опирающегося на плоскость и подвешенного на нити. Заменим тело точкой 0, совпадающей с центром тяжести. 2. Приложим к точке 0 активную силу, которой является собственный вес тела G. Направим ее вниз(рис. 1, б). 3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обозначим ее R) проходит по нормали к плоскости в точке А, а реакция или усилие в нити (обозначим ее S) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересекаться в точке 0. Изобразим действующие силы в виде системы трех сходящихся сил на отдельном чертеже (рис. 1, в). 4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. 1, г). Определим углы между осями координат и реакциями R и S. Обычно рис. 1, б и 1, в не выполняют отдельно, a сразу от рис. 1, а переходят к рис. 1, г. Можно было ось у совместить с усилием и ось х направить по углом 90°, тогда решение было бы другим. 5. Составим сумму проекций всех сил на оси координат: 1) 2) Решим систему уравнений. Из второго уравнения находим 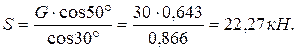 Из первого уравнения находим 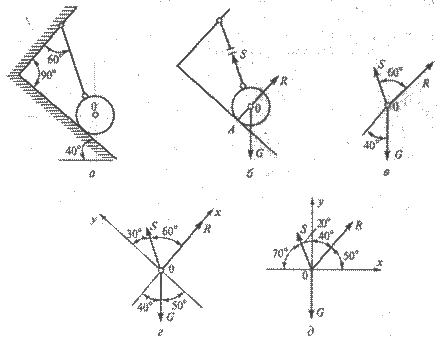 Рис. 1 6. Проверим решение, для чего расположим оси координат, как показано на рис. 1, д. Составим уравнения равновесия для вновь принятых осей: 1) 2) Решим систему уравнений способом подстановки. Из первого уравнения найдем R: Подставим это выражение во второе уравнение:  откуда 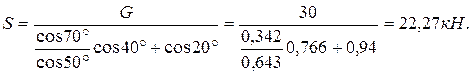 Теперь найдем R: Ответ: R=11,84 кН; S=22,27 кН. Задание. Определить величину и направление реакций связей для схемы. 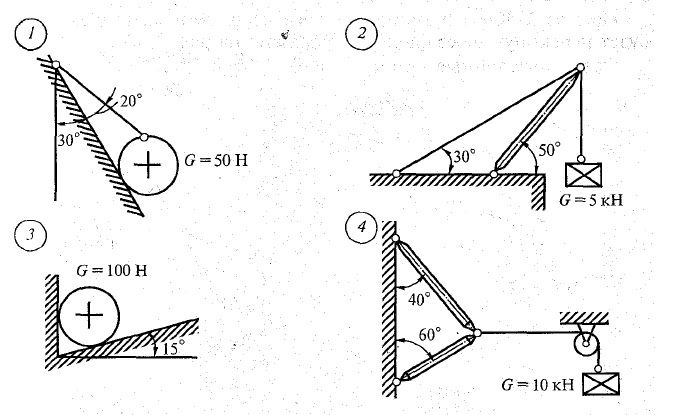 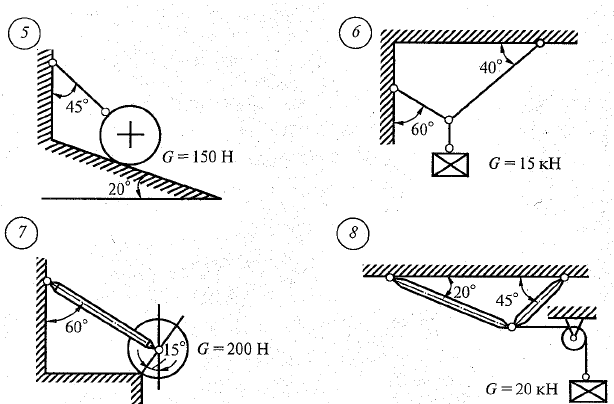 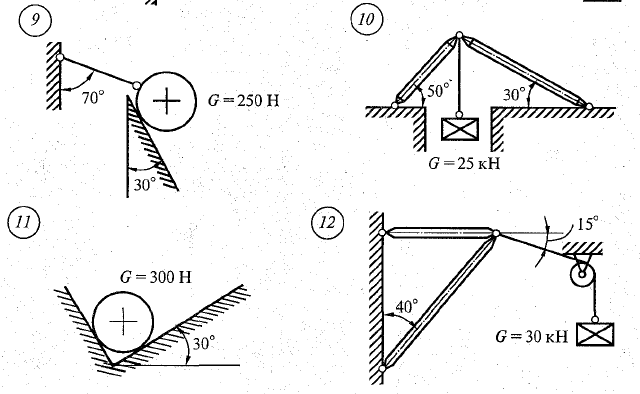 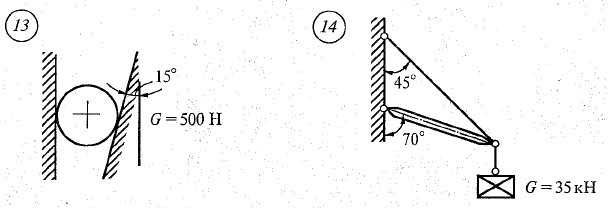 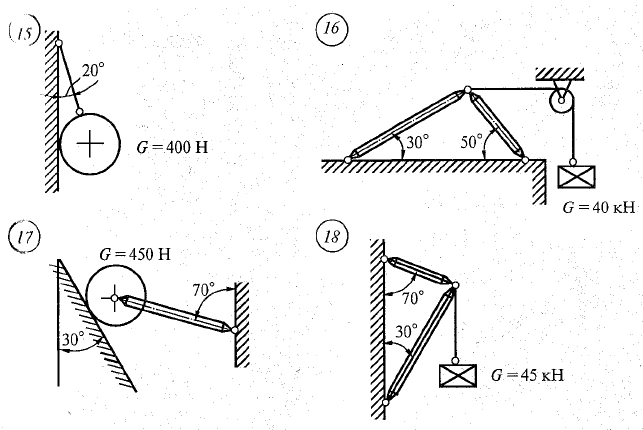 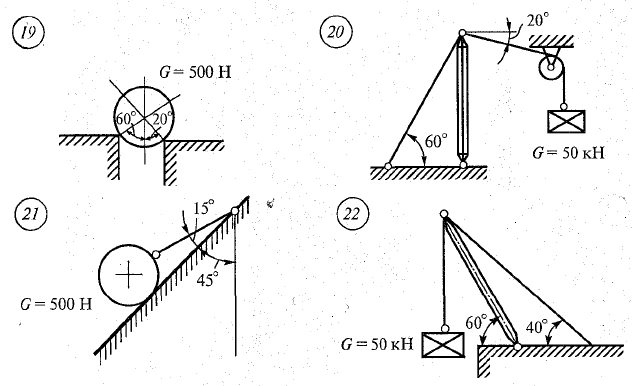 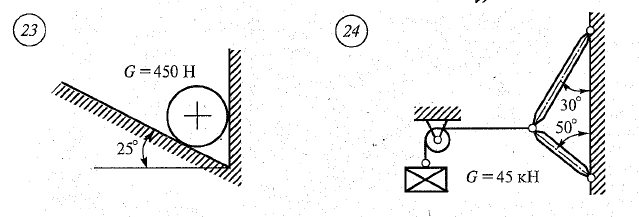 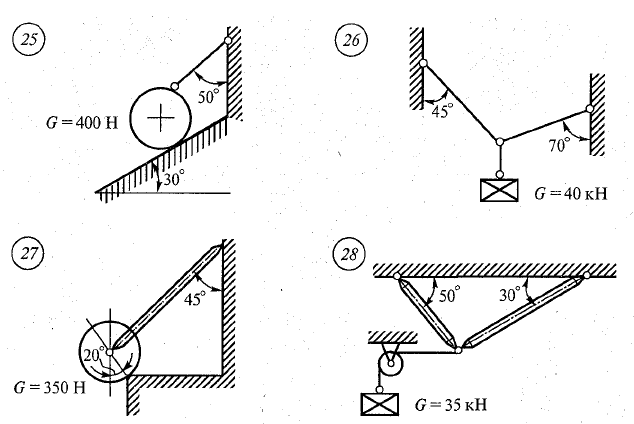 Контрольные вопросы. Что называется связью? Перечислите основные виды опор. Запишите аксиому связей. Как направлена реакция гибкой нити? |
