Логические величины и выражения. Практическая работа 2 "Программирование логических выражений"

• Название: Практическая работа 2 "Программирование логических выражений"
• Дата: 18.02.2019
• Размер: 280.5 Kb.
• Имя файла: Логические величины и выражения.doc
• Тип: Практическая работа; #67982

Логические величины и выражения, программирование ветвлений
Практикум
Практическая работа № 3.2
"Программирование логических выражений"



К числу основных понятий логики относятся: высказывание, логическая величина, логические операции, логические выражения и формулы.

Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывании можно сказать, истинно оно или ложно.

Например, высказывание «На улице идет дождь» будет истинным или ложным в зависимости от состояния погоды в данный момент. Истинность высказывания «Значение А больше, чем В», записанного в форме неравенства: А > В, будет зависеть от значений переменных А и В.

Логические величины — понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно,истинность высказываний выражается через логические величины.

Логическая константа: ИСТИНА или ЛОЖЬ.

Логическая переменная: символически обозначенная логическая величина. Следовательно, если известно, что А, В, X, Y и др. — переменные логические величины, то, значит, они могут принимать значения только ИСТИНА или ЛОЖЬ.

Логическое выражение — простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок). 

Логические операции

Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки & или ∧. Конъюнкция — двухместная операция; записывается в виде: А & В. Значением такого выражения будет ЛОЖЬ, если значение хотя бы одного из операндов ложно.

Дизъюнкция (логическое сложение). В русском языке этой связке соответствует союз ИЛИ. В математической логике она обозначается знаком v. Дизъюнкция — двухместная операция; записывается в виде: A v В. Значением такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.

Отрицание. В русском языке этой связке соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что ...»). Отрицание — унарная (одноместная) операция; записывается в виде: ¬ А или Ā.

Правила выполнения рассмотренных логических операций отражены в следующей таблице, которая называется таблицей истинности логических операций (здесь И означает «истина», Л — «ложь»):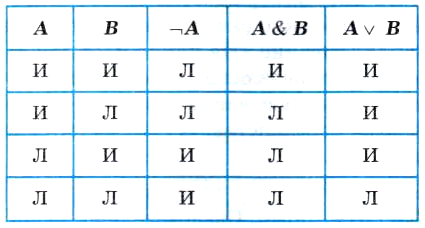



Логическая формула— формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.

Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок выполнения операций влияют скобки, которые можно использовать в логических формулах.

Например: (А & В) v (¬ А & В) v (¬ А & ¬ В).
Пример. Вычислить значение логической формулы:

¬ X & Y v X & Z,

если логические переменные имеют следующие значения: X = ЛОЖЬ, Y = ИСТИНА, Z = ИСТИНА.

Решение. Отметим цифрами сверху порядок выполнения операций в формуле:



Используя таблицу истинности, вычислим формулу по шагам:

1) ЛОЖЬ = ИСТИНА;

2) ИСТИНА & ИСТИНА = ИСТИНА;

3) ЛОЖЬ & ИСТИНА = ЛОЖЬ;

4) ИСТИНА v ЛОЖЬ = ИСТИНА.

Ответ: ИСТИНА.

Логические функции на области числовых значений

Алгебра чисел пересекается с алгеброй логики в тех случаях, когда приходится проверять принадлежность значений алгебраических выражений некоторому множеству. Например, принадлежность значения числовой переменной X множеству положительных чисел выражается через высказывание: «X больше нуля». Символически это записывается так: Х > 0. В алгебре такое выражение называют неравенством. В логике — отношением.

Отношение X > 0 может быть истинным или ложным. Если X — положительная величина, то оно истинно, если отрицательная, то ложно. В общем виде отношение имеет следующую структуру:

< выражение 1 > < знак отношения > < выражение 2 >

Здесь выражения 1 и 2 — некоторые математические выражения, принимающие числовые значения. В частном случае выражение может представлять собой одну константу или одну переменную величину. Знаки отношений могут быть следующими:



Итак, отношение — это простое высказывание, а значит, логическая величина. Оно может быть как постоянной: 5 > 0 — всегда ИСТИНА, 3 * 6 : 2 — всегда ЛОЖЬ; так и переменной: а < b, х + 1 = с - d. Если в отношение входят переменные числовые величины, то и значение отношения будет логической переменной.

Отношение можно рассматривать как логическую функцию от числовых аргументов. Например: F(x) = (х > 0) или Р(х, у) = = (х < у). Аргументы определены на бесконечном множестве действительных чисел, а значения функции — на множестве, состоящем из двух логических величин: ИСТИНА, ЛОЖЬ.

Логические функции от числовых аргументов еще называют термином предикат. В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.
Пример 1. Записать предикат (логическую функцию) от двух вещественных аргументов X и Y, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и Y лежит внутри единичной окружности с центром в начале координат (рис. 3.12).

Из геометрических соображений понятно, что для всех точек, лежащих внутри единичной окружности, будет истинным значение следующей логической функции:

F(Х, У) = (X² + У² < 1).

Для значений координат точек, лежащих на окружности и вне ее, значение функции F будет ложным.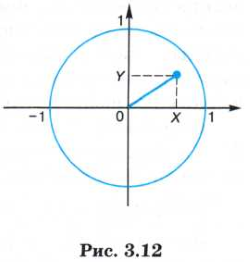



Пример 2. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри кольца с центром в начале координат, и радиусами R1 и R2.

Поскольку значения R1 и R2 — переменные величины, искомая логическая функция будет иметь четыре аргумента: X, У, R1, R2. Возможны две ситуации:

1) R1² < X² + У² < R2² и R1 < R2: R1 — внутренний радиус, R2 — внешний радиус;

2) R2² < X² + У² < R1² и R2 < R1: R2 — внутренний радиус, R1 — внешний радиус.

Объединив дизъюнкцией оба этих утверждения и записав их по правилам алгебры логики, получим следующую логическую функцию:

F(Х, У, R1, R2) = (((X² + У²) > R1²) & ((X² + У²) < R2²) & R1 < R2) v (((X² + У²) > R2²) & ((X² + У²) < R1²) & R2 < R1).
Пример 3. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри фигуры, ограниченной жирными линиями на рис. 3.13.

Фигура ограничена тремя границами, описываемыми уравнениями:

У = -X — левая граница, линейная функция;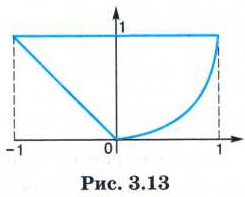

У = 1 — верхняя граница, константа;

У = X² — правая граница, парабола.

Рассматриваемая область есть пересечение трех полуплоскостей, описываемых неравенствами: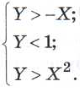



Во внутренних точках все эти три отношения являются одно-временно истинными. Поэтому искомый предикат имеет вид:

F(X, У) = (У > -X) & (Y < 1) & (У > X²). 

Логические выражения на Паскале

Уже говорилось о том, что в Паскале имеется логический тип данных.

Логические константы: true (истина), false (ложь).

Логические переменные: описываются с типом Boolean.

Операции отношения: осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними. Знаки операций отношения: = (равно), <> (не равно), > (больше), < (меньше), >= (больше или равно), <= (меньше или равно).

Логические операции: not — отрицание, and — логическое умножение (конъюнкция), or — логическое сложение (дизъюнкция), хоr — исключающее ИЛИ. Таблица истинности для этих операций (Т — true; F — false)

Логическое выражение может состоять из логических констант и переменных, отношений, логических операций. Логическое выражение принимает значение true или false.

Например, логическая формула ¬ X & У v X & Z на Паскале запишется в виде следующего логического выражения:

not X and Y or X and Z,

где X, Y, Z — переменные типа Boolean.

Логические операции располагаются в следующем порядке по убыванию старшинства (приоритета): 1) not, 2) and, 3)or, xor. Операции отношения имеют самый низкий приоритет. Поэтому если операндами логической операции являются отношения, то их следует заключать в круглые скобки. Например, математическому неравенству 1 ≤ X ≤ 50 соответствует следующее логическое выражение:

(1 <= Х) and (Х <= 50)

Логическая функция odd(x) принимает значение true, если значение целочисленного аргумента х является нечетным, иначе — false.

Для правильной записи сложного логического выражения (предиката) нужно учитывать относительные приоритеты арифмети-ческих, логических операций и операций отношений, поскольку все они могут присутствовать в логическом выражении. По убыванию приоритета операции располагаются в следующем порядке.

1. Арифметические операции:

- (минус унарный)

*, /

+, -

2. Логические операции:

not

and

or, xor

3. Операции отношения:

=, <>, >, <, >=, <=
Еще раз обратите внимание, что в логическом выражении, соответствующем предикату из примера 3:

(Y > -X) and (Y < 1) and (Y > X * X),

операции отношения заключены в скобки, поскольку они младше логических операций, а выполняться должны раньше.