ПР11 Решение простейших однокритериальных задач. Практическая работа 2 Решение простейших однокритериальных задач. Методы решения многокритериальных задач
 Скачать 243.16 Kb. Скачать 243.16 Kb.
|
|
Практическая работа №2 «Решение простейших однокритериальных задач. Методы решения многокритериальных задач» Цель работы: определить оптимальное решение однокритериальных и многокритериальных задач в простейших случаях. ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ В зависимости от вида показателя эффективности различают задачи принятия решений по скалярному показателю (однокритериальные задачи) и задачи принятия решений по векторному показателю (многокритериальные задачи). Задачами математического программирования называют однокритериальные задачи оптимизации. Методы их решения оперируют с детерминированными математическими моделями. В этих моделях отражены разнообразные проблемы распределения ограниченных ресурсов в экономике, военном деле, создании новой техники и т.д. Пути решения этих проблем, так или иначе, связаны с планированием целенаправленной деятельности, т.е. с разработкой определенных установок на будущее. Задача математического программирования формулируется следующимобразом: найти значения переменных Различают два вида задач математического программирования: Задачи линейного программирования. Задачи нелинейного программирования. В первых задачах функция Графоаналитический метод решения задач оптимизации Этим методом вручную решаются простые задачи оптимизации. Математические модели в этих задачах не должны быть сложными, т.к. в противном случае требуется много времени для их решения. Для начала рассмотрим однопараметрическую однокритериальную задачу оптимизации. Постановка задачи: Дан один критерий и т.д. Необходимо найти оптимальное значение параметра Задача решается в два этапа: Построение области допустимых решений (ОДР). Нахождение в пределах ОДР оптимального решения. При построении ОДР на первом этапе рассматривается система ограничений. Все ограничения должны быть выполнены. Выполнение первого ограничения в приведенной выше постановке задачи оптимизации означает, что искомое значение параметра 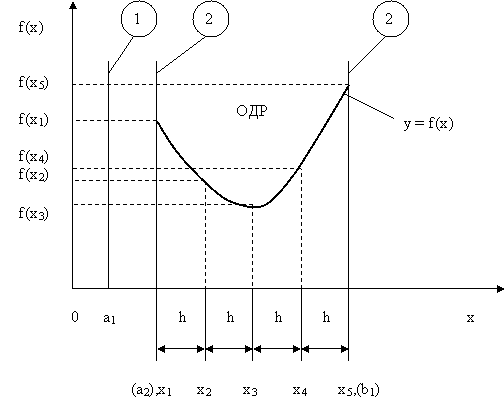 Рис.1. Графическая иллюстрация решения однопараметрической однокритериальной задачи оптимизации Когда однопараметрическая однокритериальная задача оптимизации решается с применением графоаналитического метода вручную, то на втором этапе применяют метод перебора. Суть его заключается в следующем. В пределах ОДР через определенный интервал h выбирается ряд значений параметра При решении практических задач оптимизации всегда следует иметь в виду, какова целевая функция. Это значительно упрощает работу как при решении задач оптимизации вручную с применением графоаналитического метода, так и при решении таких задач с использованием компьютерных программ. Причем, это относится и к случаю использования готовых программ, и, что особенно важно, к разработке собственных программ. Рассмотрим, например, следующий частный случай, когда целевая функция линейная (рис.2.). 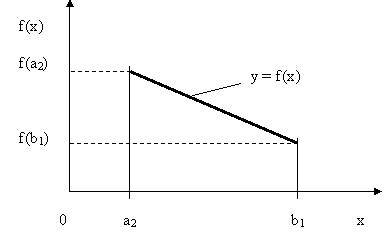 Рис.2. Графическая иллюстрация решения однопараметрической однокритериальной задачи оптимизации для случая линейной целевой функции В данном случае на втором этапе вычисляют значения целевой функции только на границах ОДР. Эти значения сравнивают и выбирают наименьшее или наибольшее. Для примера, приведенного на рис. 2, если В задачах, как правило, присутствует не один, а несколько признаков предпочтения (критериев). Такие задачи называются многокритериальными. Критерии могут оказаться противоречивыми, т.е. решение, лучшее по определенному признаку, может оказаться худшим по другому признаку. Например, минимизация стоимости и максимизация качества товара почти всегда противоречивы. В этом случае задача отыскания решения, предпочтительного по всем признакам, будет некорректной, т.е. не будет иметь ни одного решения. В случае противоречивых критериев имеются следующие подходы к отысканию подходящего решения. 1) Замена некоторых критериев ограничениями вида ≤ или ≥ . Например, минимизация стоимости f (x) → min, может быть заменена ограничением вида f (x) ≤ A, где A некоторая верхняя оценка стоимости, т.е. максимально допустимая стоимость. 2)Свертка критериев. Создается один глобальный скалярный критерий, целевая функция которого является некоторой функцией от исходных целевых функций. Наиболее употребимыми являются линейные свертки вида αf(x) + βg(x) (в случае двух критериев). Нетривиальной является задача отыскания адекватных значений коэффициентов α и β , отражающих относительную важность целевых функций f (x) и g (x). 3) Ранжирование критериев. Критерии ранжируются по степени важности. 4) Отыскание решений, лучших хотя бы по одному критерию. Подходы 1) и 2) приводят к однокритериальной задаче. Подход 3) приводит к задаче с упорядоченными критериями. Подход 4) приводит к задаче с независимыми критериями. В задаче с упорядоченными критериями критерии упорядочиваются по важности, и требуется найти оптимальное решение для наименее важного критерия на множестве решений, оптимальных для более важного критерия (см. рис 3). Самое большое множество 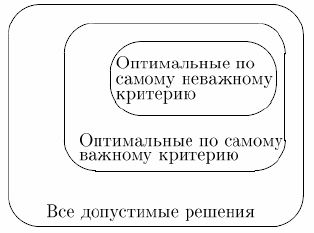 Рис 3. Множество решений. всех допустимых решений, в него вложено множество решений, оптимальных по самому важному критерию, далее вложено множество оптимальных решений по второму по важности критерию, и т.д. В задаче с независимыми критериями требуется найти множество недоминируемых (эффективных) решений. Недоминируемое решение лучше любого другого допустимого решения хотя бы по одному критерию либо не хуже по всем критериям. Множество недоминируемых решений также называется множеством Парето. Порядок выполнения заданий Задание 1. Решить графическим способом задачу. Для производства двух видов, изделии 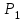 и и 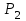 используется, три вида сырья используется, три вида сырья 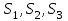 , запасы которого соответственно равны 100, 60, 180 единиц. Для производства одной единицы продукции , запасы которого соответственно равны 100, 60, 180 единиц. Для производства одной единицы продукции 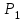 используется 2 единицы сырья используется 2 единицы сырья 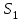 и по 1 единице сырья и по 1 единице сырья 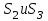 . Для производства одной единицы продукции . Для производства одной единицы продукции 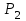 используется по 1 единице сырья используется по 1 единице сырья  и 4 единицы сырья и 4 единицы сырья 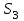 . Прибыль от реализации 1 единицы каждой продукции . Прибыль от реализации 1 единицы каждой продукции 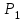 и и 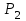 соответственно равна 30 и 20 единиц. Необходимо составить такой план выпуска продукции соответственно равна 30 и 20 единиц. Необходимо составить такой план выпуска продукции 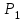 и и 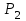 , при котором суммарная прибыль будет наибольшей. , при котором суммарная прибыль будет наибольшей.Решение. Составим математическую модель задачи: Пусть х1 – единица готовой продукции вида 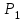 , ,x2 - единица готовой продукции вида 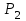 , ,Цель фабрики получить максимальную прибыль от реализации всей продукции видов 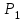 и и 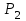 , тогда: , тогда: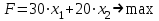 Система ограничений: 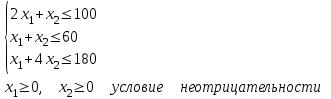 Алгоритм решения: Используя систему ограничений и условия неотрицательности, строим область допустимых решений. Строим линию уровня 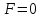 . Линией уровня функции двух переменных называется линия, вдоль которой функция сохраняет свое постояное значение. . Линией уровня функции двух переменных называется линия, вдоль которой функция сохраняет свое постояное значение.Строим градиент целевой функции. Градиент функции - это вектор, имеющий своими координатами частные производные функции и показывающий направление наискорейшего роста значения функции. Так как целевая функция ЗЛП линейная, то линии уровня целевой функции - прямые и 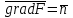 , п- вектор нормали к этим прямым. : . , п- вектор нормали к этим прямым. : . Перемещаем линию уровня 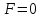 вдоль градиента функции. Если ЗЛП на минимум, то оптимальное решение находится в первой точке, принадлежащей ОДР; если ЗЛП на максимум, то оптимальное решения находится в последней точке, принадлежащей ОДР. вдоль градиента функции. Если ЗЛП на минимум, то оптимальное решение находится в первой точке, принадлежащей ОДР; если ЗЛП на максимум, то оптимальное решения находится в последней точке, принадлежащей ОДР.Замечание. При построении ОДР возможны случаи: ОДР оказалась пустым множеством. В этом случае ЗЛП не имеет решения из-за несовместности системы ограничений. ОДР оказалась либо выпуклым многоугольником, либо не ограниченной выпуклой многоугольной областью. Тогда ЗЛП имеет оптимальное решение, которое совпадает по крайней мере с одной из вершин ОДР. Используя алгоритм решения и систему ограничений и условия неотрицательности, построим ОДР. Для этого во всех неравенствах системы ограничений и условия неотрицательности знак неравенства заменим на знак равенства. В результате будем иметь уравнения прямых: 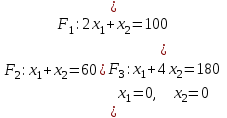 В системе координат 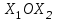 построим эти прямые. В результате будем иметь ОДР. В этой же системе координат строим линию уровня построим эти прямые. В результате будем иметь ОДР. В этой же системе координат строим линию уровня 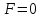 и вектор и вектор 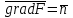 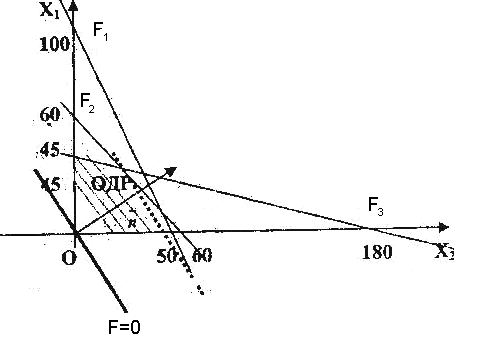 Так как задача на максимум, будем перемещать линию уровня F=0 вдоль вектора n до тех пор, пока она не пересечет ОДР в самом крайнем своем положении, т.е. при дальнейшем перемещении она не будет с ОДР иметь общие точки. Такой точкой оказалась точка пересечения прямых 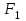 и и 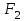 . .Вычислим ее координаты. 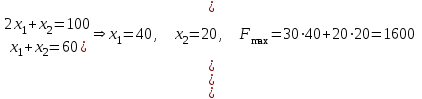 Таким образом, если предприятие будет выпускать продукцию вида 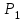 и и 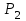 , в количестве 40 и 20 единиц соответственно, то получит максимальную прибыль в размере 1600 единиц. , в количестве 40 и 20 единиц соответственно, то получит максимальную прибыль в размере 1600 единиц. Задание 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки.   Задания для самостоятельной работы 1 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 19, а2= 16, а3= 19, b1= 26, b2= 17, b3= 8, c1= 868, c2= 638, c3= 853, α=5, β=4. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев 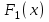 и и 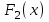 и определить минимальное решение. и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида 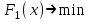 и и 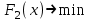 . .Значения 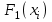 и и 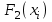 заданы таблицей: заданы таблицей:
2 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев 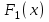 и и 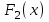 и определить минимальное решение. и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида 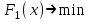 и и 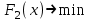 . .Значения 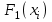 и и 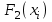 заданы таблицей: заданы таблицей:
3 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 9, а2= 15, а3= 15, b1= 27, b2= 15, b3= 3, c1= 606, c2= 802, c3= 840, α=11, β=6. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев 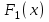 и и 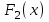 и определить минимальное решение. и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида 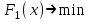 и и 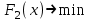 . .Значения 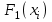 и и 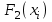 заданы таблицей: заданы таблицей:
4 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 13, а2= 13, а3= 11, b1= 23, b2= 11, b3= 1, c1= 608, c2= 614, c3= 575, α=5, β=7. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев 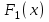 и и 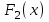 и определить минимальное решение. и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида 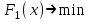 и и 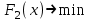 . .Значения 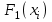 и и 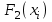 заданы таблицей: заданы таблицей:
5 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 19, а2= 16, а3= 19, b1= 31, b2= 9, b3= 1, c1= 1121, c2= 706, c3= 1066, α=16, β=19. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев 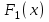 и и 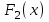 и определить минимальное решение. и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида 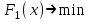 и и 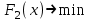 . .Значения 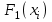 и и 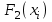 заданы таблицей: заданы таблицей:
Контрольные вопросы Какие задачи называются однокритериальными? Какие задачи называются многокритериальными? Какие способы решения однокритериальных задач вы знаете? Какие подходы к отысканию подходящего решения вы знаете у противоречивых критериев? Какое множество называется множеством Парето? |