Практическая работа 24. Сетевое и системное администрирование. ПР 24. Практическая работа 24 Вычисление экстремумов функций нескольких переменных
 Скачать 35.22 Kb.
|
|
Практическая работа №24 «Вычисление экстремумов функций нескольких переменных» Цель: Освоить применение частных производных для нахождения экстремумов функции нескольких переменных Теоретические сведения по выполнению практической работы: Пусть функция z = ƒ(х;у) определена в некоторой области D, точка N(x0;y0) Î D. Точка (х0;у0) называется точкой максимума функции z=ƒ(х;у), если существует такая d-окрестность точки (х0;у0), что для каждой точки (х;у), отличной от (хо;уо), из этой окрестности выполняется неравенство ƒ(х;у)<ƒ(хо;уо). А 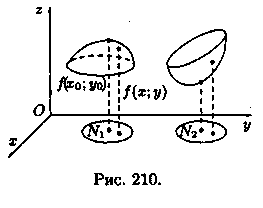 налогично определяется точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>ƒ(х0;у0).На рисунке 210: N1 — точка максимума, а N2 — точка минимума функции z=ƒ(x;у). Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами. Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (х0;у0) сравнивается с ее значениями в точках, достаточно близких к (х0; у0). В области D функция может иметь несколько экстремумов или не Необходимые и достаточные условия экстремума Рассмотрим условия существования экстремума функции. Теорема (необходимые условия экстремума). Если в точке N(x0;y0) дифференцируемая функция z=ƒ(х;у) имеет экстремум, то ее частные производные в этой точке равны нулю: ƒ'x(х0;у0)=0, ƒ'y(х0;у0)=0. Зафиксируем одну из переменных. Положим, например, у=у0. Тогда получим функцию ƒ(х;у0)=φ(х) одной переменной, которая имеет экстремум при х = х0. Следовательно, согласно необходимому условию экстремума функции одной переменной (см. п. 25.4), φ'(х0) = 0, т. е. ƒ'x(х0;y0)=0. Аналогично можно показать, что ƒ'y(х0;у0) = 0. Геометрически равенства ƒ'x(х0;у0)=0 и ƒ'y(х0;у0)=0 означают, что в точке экстремума функции z=ƒ(х;у) касательная плоскость к поверхности, изображающей функцию ƒ(х;у), параллельна плоскости Оху, т. к. уравнение касательной плоскости есть z=z0 (см. формулу (45.2)). З  амечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция имеет максимум в точке О(0;0) (см. рис. 211), но не имеет в этой точке частных производных.Точка, в которой частные производные первого порядка функции z ≈ ƒ(х; у) равны нулю, т. е. f'x=0, f'y=0, называется стационарной точкойфункции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка О(0; 0) является критической (в ней z'x=у и z'y — х обращаются в ноль). Однако экстремума в ней функция z=ху не имеет, т. к. в достаточно малой окрестности точки О(0; 0) найдутся точки для которых z>0 (точки I и III четвертей) и z < 0 (точки II и IV четвертей). Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию. Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке (хо;уо) и некоторой ее окрестности функция ƒ(х;у) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0;у0) значения A=f''xx(x0;y0), В=ƒ''xy(х0;у0), С=ƒ''уy(х0;у0). Обозначим 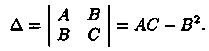 Тогда: 1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А< 0; минимум, если А > 0; 2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет. В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования. Вариант № 1 Найдите экстремумы для следующих функций: 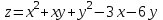 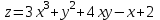 Запишите необходимые условия существования экстремума Вариант № 2 Найдите экстремумы для следующих функций: 1) 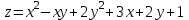 2) 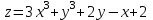 Запишите достаточные условия существования экстремума в точке |