Мат анализ. Задача Исследовать функцию на непрерывность и построить схематично график. Данные к условию задачи Решение
 Скачать 446.31 Kb. Скачать 446.31 Kb.
|
|
Вариант № 19 Задача 4.8. Исследовать функцию на непрерывность и построить схематично график. Данные к условию задачи: 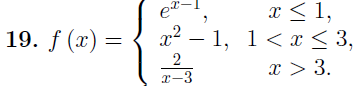 Решение: Функция определена на всей числовой оси, но из этого не следует, что она непрерывна на всей числовой оси, так как эта функция неэлементарная. Она задана тремя различными формулами для разных интервалов изменения аргумента 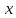 , и может иметь разрыв в точках , и может иметь разрыв в точках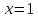 и и 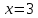 , где меняется ее аналитическое выражение. , где меняется ее аналитическое выражение.1) Исследуя точку 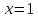 , находим односторонние пределы функции при стремлении , находим односторонние пределы функции при стремлении 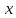 к этой точке слева и справа. к этой точке слева и справа.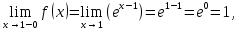 так как слева от точки 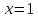 функция имеет вид: функция имеет вид: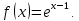 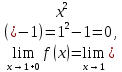 так как справа от точки 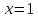 функция функция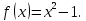 Левый и правый пределы конечны, но не равны между собой. Поэтому функция в этой точке имеет разрыв 1-го рода (скачок). 2) Исследуя точку 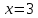 , находим односторонние пределы функции при стремлении , находим односторонние пределы функции при стремлении 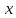 к этой точке слева и справа. к этой точке слева и справа.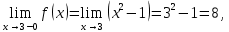 так как слева от точки 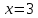 функция имеет вид: функция имеет вид: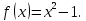 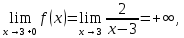 так как справа от точки 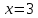 функция функция Один из пределов бесконечен. Поэтому функция в этой точке имеет разрыв 2-го рода.  Ответ: в точке х = 1 функция имеет разрыв 1-го рода (скачок на (-1) единицу), в точке х = 3 функция терпит разрыв 2-го рода. Задача 5.1. Найти производную: а) сложной функции; б) логарифмическим дифференцированием; в) параметрически заданной функции. Данные к условию задачи: 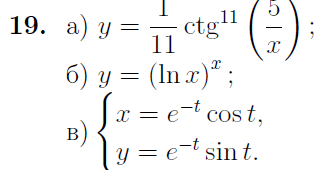 а) 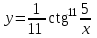 Используем формулы дифференцирования: 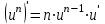 ; ;  ; ; 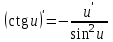 . .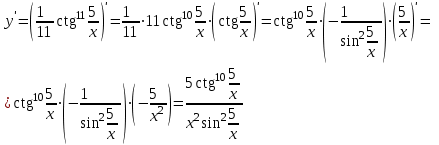 Ответ: 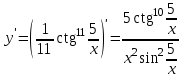 б) 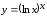 Используем метод логарифмического дифференцирования : находим логарифм обоих частей, а потом находим производную от обоих частей, считая, что 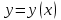 . .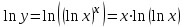 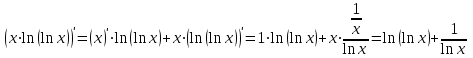 Тогда: 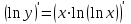 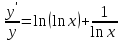 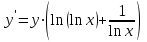 Подставляем вместо у его значение 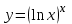 Ответ: 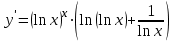 . . в)  . Функция задана параметрически . Функция задана параметрически 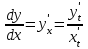 . .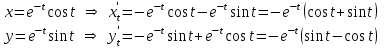 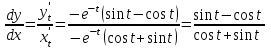 . .Ответ: 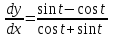 . .Задача 5.2. Дано уравнение кривой. Составить уравнения касательной и нормали в точке с абсциссой x = x0. Данные к условию задачи: Решение: Уравнение касательной: 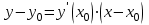 . .Уравнение нормали: 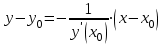 . .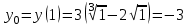 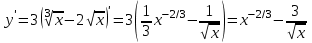 , , 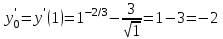 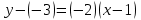 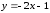 касательная. касательная.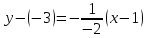 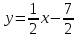 – нормаль – нормаль Задача 5.3. Вычислить приближенно значение функции y = f(x) при заданном значении х. Данные к условию задачи: Решение: 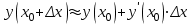 Тут 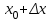 = 8,06 = 8 + 0,06 х0 = 8; Δх = 0,06; = 8,06 = 8 + 0,06 х0 = 8; Δх = 0,06; 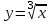 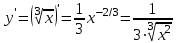 ; ;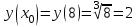 ; ; 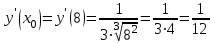 ; ; 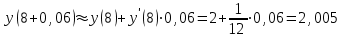 . .Ответ: 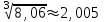 . . Задача 5.4. Найти наибольшее и наименьшее значения функции на отрезке. 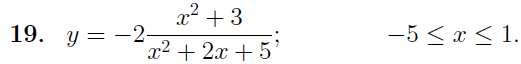 Решение: 1) Находим критические точки функции 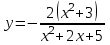 , которые лежат на данном отрезке. Для этого вычисляем первую производную , которые лежат на данном отрезке. Для этого вычисляем первую производную 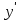 и приравниваем ее к нулю: и приравниваем ее к нулю: 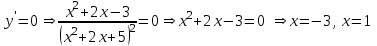 . .2) Вычисляем значение функции 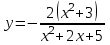 в критической точке, а также на концах отрезка, а потом выбираем среди найденных значений наибольшее и наименьшее: в критической точке, а также на концах отрезка, а потом выбираем среди найденных значений наибольшее и наименьшее: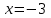 Þ Þ 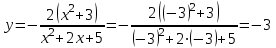 минимальное значение минимальное значение правый конец интервала : 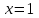 Þ Þ  ← максимальное значение. ← максимальное значение. левый конец интервала: 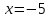 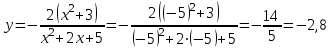 Ответ:  при при 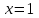 ; ; 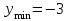 при при 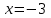 . .Задача 5.5. Решить следующие задачи на наибольшее и наименьшее значения. Данные к условию задачи: 19. Напряжение на клеммах электрической цепи, равное первоначально нулю, равномерно возрастает, одновременно в цепь вводится сопротив- ление, пропорциональное квадрату времени с коэффициентом пропорци- ональности 9 Ом/мин. Первоначальное сопротивление цепи равно 1 Ом. В какой момент времени ток в цепи наибольший. Решение: Для решения задачи применяется закон Ома. Напряжение в любой момент времени t согласно условию задачи можно записать так: U(t) = 0 + kt, где k – коэффициент пропорциональности. Сопротивление в любой момент времени запишем так: R(t) = r0 + k1t2, где R0 – начальное сопротивление, k1 – указанный коэффициент пропорциональности. Закон Ома 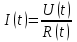 , где U(t) = kt, R(t) = r0 + 9t2, по условию первоначальное сопротивление цепи равно 1 Ом, т.е. r0 = 1. , где U(t) = kt, R(t) = r0 + 9t2, по условию первоначальное сопротивление цепи равно 1 Ом, т.е. r0 = 1.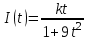 , нужно найти наибольшее значение этой функции, для этого находим первую производную и приравниваем её к нулю: , нужно найти наибольшее значение этой функции, для этого находим первую производную и приравниваем её к нулю: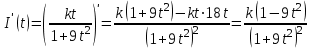 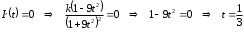 Ответ: t = 1/3 с. Задача 5.6. Найти асимптоты кривой, заданной уравнением. Данные к условию задачи: 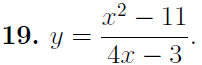 Решение: Область определения D: х 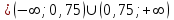 , то есть функция существует на всей числовой оси кроме точки , то есть функция существует на всей числовой оси кроме точки 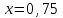 . .а) Так как  , то х = 0,75 – вертикальная асимптота. , то х = 0,75 – вертикальная асимптота.б) 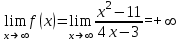 , поэтому горизонтальных асимптот нет. , поэтому горизонтальных асимптот нет.в) Формула для наклонных асимптот: 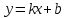 , где , где 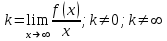 ; ; 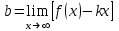 . .Здесь k = 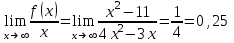 ; ; 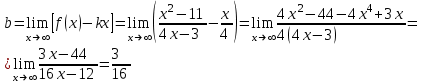 Итак, наклонная асимптота имеет уравнение 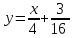 . .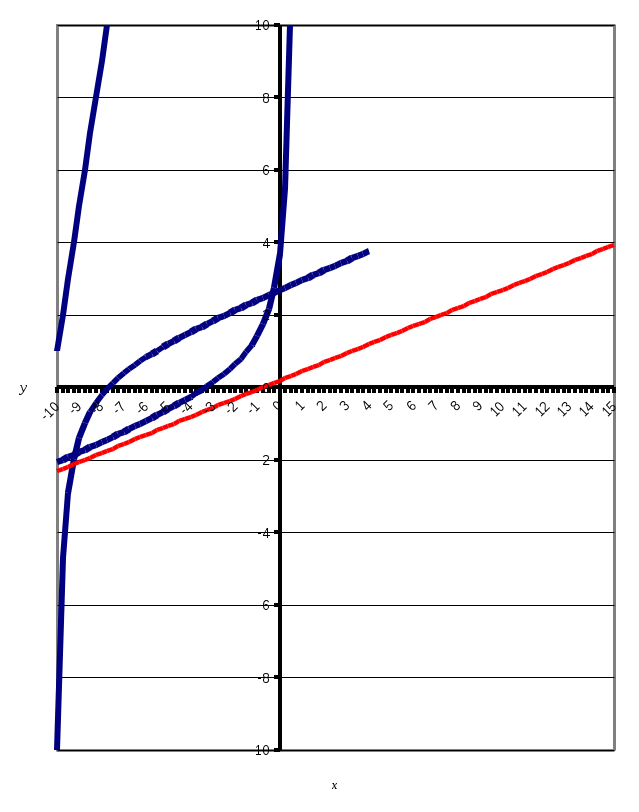 Ответ: 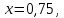 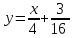 . .Задача 5.7. Провести полное исследование и построить график функции. Решение: 1) Область определения D: х 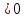 , то есть функция существует на всей числовой оси, кроме точки х = 0. Это точка разрыва 2-го рода. , то есть функция существует на всей числовой оси, кроме точки х = 0. Это точка разрыва 2-го рода.2) Четность: 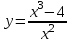 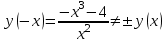 , то есть функция общего вида. , то есть функция общего вида.3) Интервалы роста и убывания функции, точки экстремума. Находим первую производную и приравниваем ее к нулю: 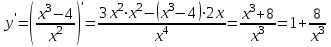 ; ; 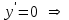 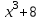 = 0; х = 0; х 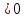 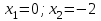 – критические точки. – критические точки.Находим значение функции в критических точках: 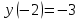 Полученные данные заносим в таблицу:
4) Точка перегиба, интервалы выпуклости и вогнутости. Находим вторую производную и приравниваем ее к нулю: 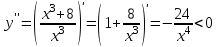 для всех х функция выпуклая на своей области определения, точек перегиба нет. В точке х = 0 функция не определена. для всех х функция выпуклая на своей области определения, точек перегиба нет. В точке х = 0 функция не определена.5) Функция не имеет горизонтальных асимптот, потому что 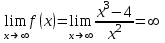 . .Вертикальная асимптота х = 0 , потому что х = 0 – точка разрыва 2-го рода: 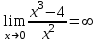 . .Формула для наклонных асимптот : 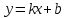 , , где 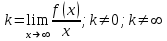 ; ; 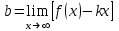 . .Здесь k = 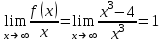 ; ; 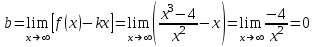 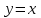 – наклонная асимптота. – наклонная асимптота.Используя полученные данные, строим график функции 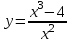 : : 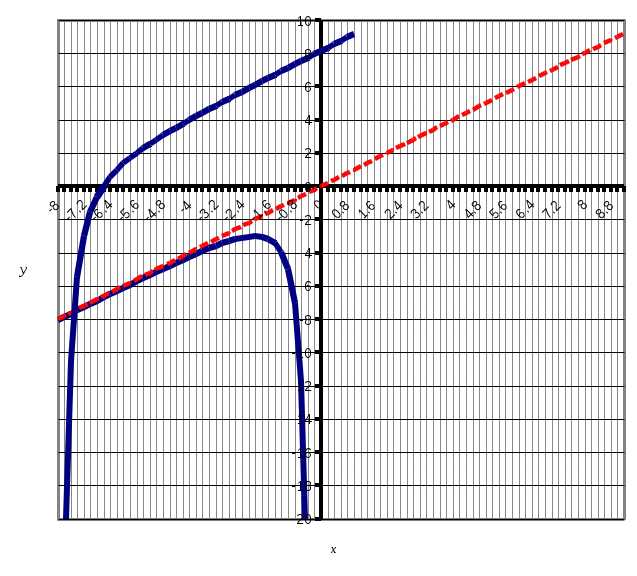 Задача 5.8. По графику функции построить эскизы графиков первой и второй производных. 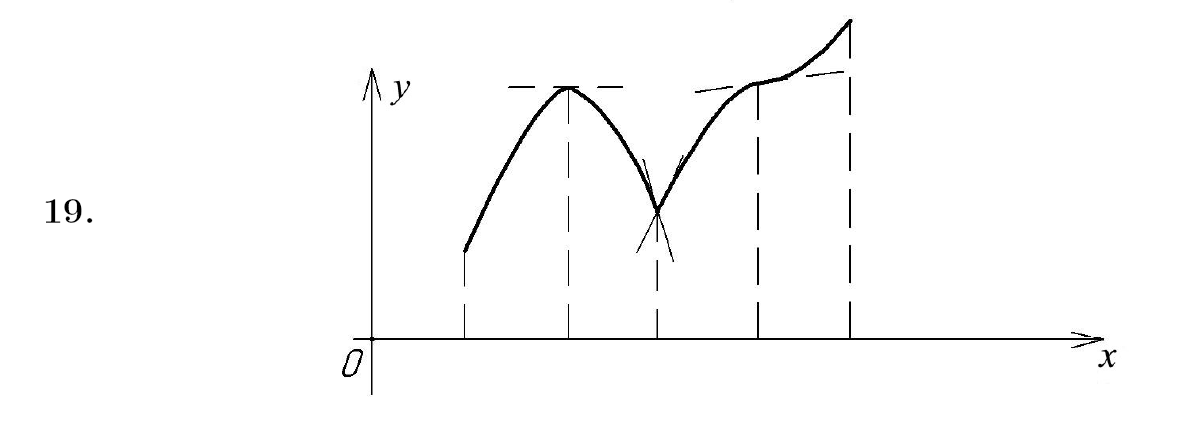 Решение: Используем геометрический смысл производной функции одного аргумента: производная функции, вычисленная при фиксированном значении аргумента, равна тангенсу угла, образованного осью абсцисс и касательной, проведенной к графику функции в точке вычисления производной. Если функция возрастает, то её производная положительна, если убывает, то отрицательна. В точках экстремума (когда касательная горизонтальна), производная равна нулю. В точках перегиба вторая производная равна нулю, а график первой производной имеет экстремум. Если функция выпукла, то 2-я производная отрицательна, если вогнута – то положительна.
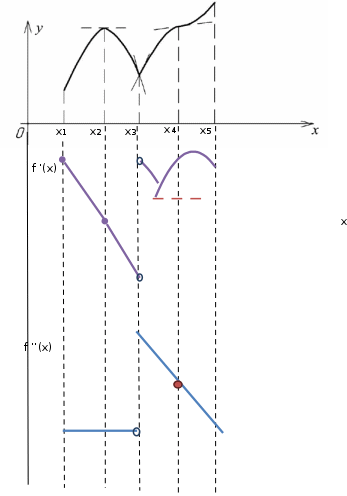 Часть 8: Задача 8.1. Найти частные производные I и II порядка заданной функции 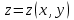 . .Решение: Находим частную производную по аргументу х, считая, что у = const : 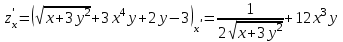 Находим частную производную 2-го порядка 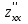 как частную производную по аргументу х от частиной производной как частную производную по аргументу х от частиной производной 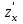 считая, что у = const : считая, что у = const :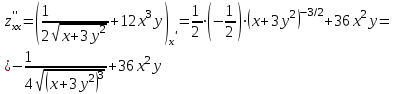 Аналогично находим 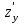 и и 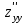 , считая, что х = const : , считая, что х = const :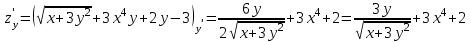 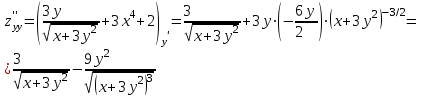 Находим смешанную производную 2-го порядка: 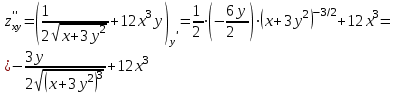 . .Задача 8.2. Используя понятие дифференциала найти приближенное значение z(x;y) в точке заданной точке M0 (х0;у0). Данные к условию задачи: Решение: Используем формулу Найдем приближенное значение 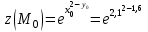 следующим образом: 1) подберем значения х1 и у1, мало отличающиеся от 2,1 и 1,6, при которых значение функции 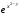 легко подсчитать: легко подсчитать: 2) находим приращение аргумента 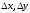 : :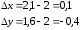 3) находим частные производные заданной функции и вычислим их значение в точке (2;2): 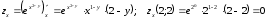 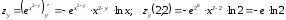 4) найденные значения подставим в формулу: 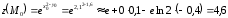 Ответ: 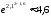 Задача 8.3. Найти локальный экстремум функции  . .Решение: Вычислим частные производные функции: 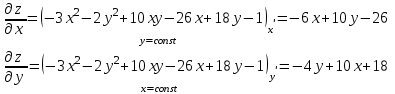 Найдем стационарные точки. Для этого решим систему уравнений:  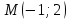 – стационарная точка. – стационарная точка.Обозначим А = 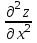 , В = , В = 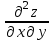 , С = , С = 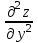 Составим выражение ∆ = АС – В². Если ∆ > 0, то при А > 0 – это будет точка mіn, а при А < 0 это будет точка mах. Если ∆ < 0, то экстремума нет. Вычислим частные производные второго порядка данной функции для критической точки: 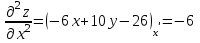 ; ; 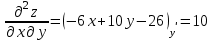 ; ; 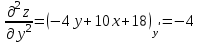 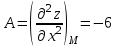 ; ; 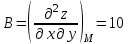 ; ; 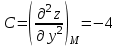 . .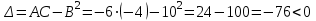 , поэтому в точке М данная функция не имеет экстремума. , поэтому в точке М данная функция не имеет экстремума.Ответ: экстремума нет. |


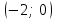
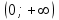
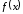
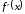
 +
+ +
+