практическая 3. Практическая работа 3 Аналитический контроль качества окружающей среды. Математическая обработка данных
 Скачать 54.79 Kb. Скачать 54.79 Kb.
|
|
Практическая работа №3 Аналитический контроль качества окружающей среды. Математическая обработка данных Задание: изучить основные стадии аналитического контроля качества окружающей среды; произвести математическую обработку полученных данных. Теоретическая часть Аналитический контроль качества окружающей среды состоит из следующих основных стадий: 1. Выбор места отбора пробы; 2. Отбор пробы; 3. Обработка пробы; 4. Измерение концентрации загрязнителя; 5. Математическая обработка данных и их проверка; 6. Интерпретация и сравнение полученных данных. Только правильная организация и проведение всех стадий обеспечивают достоверность полученной информации. Относительно выбора места отбора газообразной, жидкой или твердой пробы трудно дать общие рекомендации. При этом следует учитывать географические, геологические и экологические особенности изучаемого района, возможный характер распределения загрязнителя во времени и пространстве, метеорологические и гидрологические условия, другие объективные условия, влияющие на содержание загрязнителя в той или иной точке пространства. В каких-то случаях целесообразно "покрывать" изучаемый район сеткой с подходящим масштабом шага и брать пробы во всех узловых точках. В других случаях можно взять пробы в характерных местах с разной ожидаемой загрязненностью, например у берега реки и на стрежне, до сброса сточных вод, около него и на разных расстояниях вниз по течению. Наиболее трудной задачей, по-видимому, является выбор оптимальных точек отбора проб почвы и биоты, так как состав последних может сильно изменяться даже на малых расстояниях между точками отбора. Количество точек отбора на некоторой территории сильно зависит от технических и экономических возможностей станции, поста и т.п. При отборе пробнеобходимо получение статистически усредненного образца, что наиболее легко достигается при отборе жидкой пробы, так как она практически всегда хорошо перемешена и концентрация загрязнителя в ней достаточно однородна. Получение статистически усредненного образца твердой пробы (почва, донные отложения, биота) может быть связано с отбором одной большой пробы или ряда проб в разных точках с последующим механическим усреднением их в шаровой мельнице или путем мокрого сжигания (растворения в кислотах). Из полученного таким образом однородного материала отбирается проба необходимой для анализа массы. Статистически усредненный образец воздуха можно получить, прокачивая большие объемы его через специальные фильтры или жидкие поглотители и затем вымывая абсорбированный загрязнитель специальными растворами. Иногда фильтры-поглотители могут оголяться или анализироваться непосредственно (например, нейтронно-активационным методом). Обработка пробыможет проводиться сразу после ее отбора, ли предполагается хранение или транспортировка. В этом случае следует учитывать потери загрязнителя за счет адсорбции на стенках сосуда, оседания коллоидных частиц, химических реакций и т.п. Поэтому наиболее подходящими сосудами для сбора проб являются емкости из пищевого полиэтилена и тефлона. Жидкая проба должна наливаться "под пробку", т.е. не должно оставаться газовой фазы в сосуде. Часто рекомендуется пробу подкислять, что уменьшает адсорбцию и гидролиз. Все это касается в основном жидких проб. Твердые пробы, однако, также часто требуется изолировать от контактов с воздухом. Другие виды обработки проб связаны с концентрированием и разделением загрязнителей, что обычно делается в специальной лаборатории, а условия конкретно определяются требованиями применяемых методов анализа. Стадия "Измерение"представляет собой собственно аналитическое определение концентрации загрязнителя, включая выбор метода анализа, подготовки пробы согласно прописи выбранного метода, калибровки применяемых приборов, проверки метода с помощью стандартов, проведения холостых опытов и т.п. При проведении мониторинга следует пользоваться стандартными или общепринятыми межведомственными или ведомственными методами анализа. При отсутствии таковых необходимо самостоятельно выбрать (или даже разработать) подходящий метод. Стандартизация методов анализа в России проводится органами Госстандарта. А для обеспечения достоверности принятых методов и возможности сравнения результатов, полученных в разных лабораториях, проводится национальная и международная тарификация (интеркалибрация) аналитических методик. В ряде стран, прежде всего в США, Канаде, Японии, Нидерландах, Швейцарии и Великобритании, общепринятой является процедура "образцовой лабораторной практики" (ОЛП). Она закреплена в документах Европейского экономического сообщества (ЕЭС), в частности в Директиве № 79/831/ЕЕС-1967 и специальном документе ЕМУ/СНЕМ/МС/79:5. При выборе метода анализа из числа стандартных или при отсутствии таковых следует учитывать точность, чувствительность, предел обнаружения, селективность, производительность, другие технические и экономические показатели существующих методов. Математическая обработкаполученных данных обычно проводится следующим образом. Если х1,х2,х3...,хп- отдельные измерения искомой концентрации загрязнителя (результаты параллельных определений), то находят среднее арифметическое х по формуле: 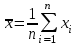 (3.1) (3.1)где п - число измерений. Затем вычисляют абсолютную случайную погрешность 1-го измерения 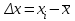 , (3.2) , (3.2)среднюю квадратическую погрешность отдельного измерения 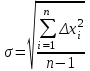 (3.3) (3.3)и относительную квадратическую погрешность отдельного измерения 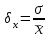 (3.4) (3.4)Из (3.3) рассчитывают среднюю квадратическую погрешность среднего арифметического  (3.5) (3.5)и относительную квадратическую погрешность среднего арифметического 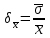 (3.6) (3.6)Истинное значение искомой концентрации загрязнителя с надежностью (вероятностью) Р лежит в доверительном интервале 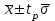 (3.7) (3.7)где tр - коэффициент Стьюдента, зависящий от числа измерений и ожидаемой (заданной) надежности P (таблица 3.1) Таблица 3.1 Коэффициент Стьюдента (tр) при принадлежности надежности (p), равной 0,95, в зависимости от числа измерений (n).
Если для некоторого i -го измерения 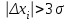 (3.8) (3.8)то это измерение отбрасывается как содержащее грубую ошибку и все величины по (3.1) - (3.7) пересчитываются заново. Ошибки любых измерений, в том числе и аналитических, могут быть: а) систематическими (в анализе они зависят от применяемого метода, неполноты протекания реакций, погрешности приборов, техники исполнения); б) случайными (зависящими от случайных загрязнений, изменений напряжения в электрической сети, изменений температуры в лаборатории, случайных изменений режима определения); в) грубыми (из-за ошибок оператора, поломок аппаратуры и т.п.). Систематические ошибки можно предвидеть и свести к минимуму, случайные учитываются при математической обработке по (3.1) - (3.7), а грубые обнаруживаются на основе критерия (3.8). Стадия "Интерпретация и сравнение полученных данных"является наиболее творческой и проводится путем анализа полученного массива результатов и их сравнения с литературными, собственными более ранними, теоретическими и другими данными. При этом анализируются возможные зависимости и взаимосвязи между концентрациями загрязнителей и другими параметрами среды. При обсуждении пригодности и вариантов применения разных аналитических методов для определения концентрации загрязнителей прежде всего обращается внимание на чувствительность и предел обнаружения этих методов. Чувствительность (Н) метода можно рассчитать по данным калибровки измерительного прибора (фотоколориметра, спектрофотометра и т.д.). При калибровке, используя растворы с известным содержанием загрязнителя, экспериментально строят зависимость некоторого фиксируемого физического параметра (оптической плотности, силы тока и т.п.) от концентрации или количества загрязнителя в пробе. На графике концентрация откладывается по оси абсцисс (х), а физический параметр - по оси ординат (у). Тогда 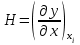 (3.9) (3.9)или 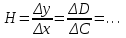 (3.10) (3.10)где D — оптическая плотность; С - концентрация, так как в аналитической химии, как правило, используется линейная часть градуировочного графика. Предел обнаружения метода (наименьшая концентрация Сm , которая может быть обнаружена с разумной достоверностью) можно рассчитать по формуле 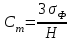 (3.11) (3.11)где σф - средняя квадратическая погрешность отдельного измерения фона yф, найденная по (3.3) и результатам экспериментального определения фона или через минимально определяемое значение физического параметра  (3.12) (3.12)по калибровочному графику. Если предел обнаружения загрязнителя выше, чем его ожидаемая концентрация в объекте окружающей среды, необходимо провести концентрирование загрязнителя. Для этой цели наиболее часто используется экстракция, реже - хроматография. Необходимый коэффициент концентрирования легко получить из сопоставления предела обнаружения метода и ожидаемой концентрации загрязнителя. Примеры решения задач на математическую обработку полученных данных Пример № 1 В семи пробах донного ила (каждая проба - 100 г) обнаружили соответственно 0,0227; 0,0237; 0,0221; 0,0232; 0,0230; 0,0265 и 0,0255 г U3O8. Проведите математическую обработку этих результатов. Найдите доверительный интервал с надежностью 95%. Примените правило 3σ для нахождения грубых ошибок. Если такие результаты есть, отбросьте их и найдите новый доверительный интервал. Решение: По уравнению (3.1) находим  = 0,0238 затем по (3.2) вычисляем ∆хi для каждого xi и получаем следующий ряд значений ∆xi : -0,0011, -0,0001, -0,0017, -0,0006, -0,0008, 0,0027 и 0,0017, из которого по (12.3) находим = 0,0238 затем по (3.2) вычисляем ∆хi для каждого xi и получаем следующий ряд значений ∆xi : -0,0011, -0,0001, -0,0017, -0,0006, -0,0008, 0,0027 и 0,0017, из которого по (12.3) находим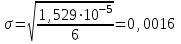 и из (3.5) 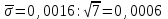 По (3.4) и (3.6) 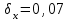 , а , а 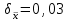 Находим tр при 7 измерениях с надежностью 0,95 и составляем доверительный интервал согласно (3.7): 0,0238 ± 2,365 ∙ 0,0006 = 0,0238 ± 0,0014. Среди значений ∆хi нет величин, превышающих 3σ = 0,0048. Пример № 2 При разработке фотоколориметрического определения бора в природных водах получили следующие результаты:
При определении фона на холостых пробах оптические плотности (Dф) оказались равными: 0,007; 0,005; 0,004; 0,008 и 0,003. Найдите чувствительность и предел обнаружения данного метода. В природных водах содержание бора обычно составляет 0,1-0,01 мг/дм3. Можно ли его определять данным методом? Решение: По данным задачи строим градуировочный график, из которого согласно (3.10) вычисляем чувствительность Н: 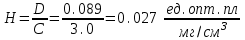 Затем так же, как в предыдущей задаче, по (3.1) и (3.3) находим Dф = 0,005 и σф = 0,002 . По (3.11) определяем предел обнаружения 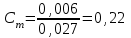 мкг/дм3 мкг/дм3или по (3.12) определяем 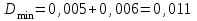 ед. опт. пл. ед. опт. пл.и по градуировочному графику находим Ст≈ 0,2 мкг/дм3 . Согласно условиям задачи концентрации бора лежат в интервале 0,01 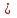 0,1 мг/дм3 = 0,01 0,1 мг/дм3 = 0,01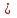 0,1 мкг/ см3. 0,1 мкг/ см3.Сравнивая эти величины с пределом обнаружения, видим, что нижний уровень концентрации в 20 раз, а верхний - в 2 раза меньше предела обнаружения, следовательно, для достижения предела обнаружения эти растворы необходимо сконцентрировать в 20 и 2 раза соответственно, а для надежного определения коэффициенты концентрирования желательно увеличить в 2-4 раза, например, при концентрировании в 60 и 6 раз. Соответственно бор будет надежно определяться как в наиболее бедных, так и в наиболее богатых им растворах. Задача 3 Для построения калибровочного графика при определении кремния были получены следующие данные:
Значения фона составили: 0,017; 0,020; 0,019; 0,017; 0,016. Найдите чувствительность и предел обнаружения метода. Какие объемы воды надо брать на анализ, если концентрации кремния лежат в области 1-75 мкг/дм3. Задача 20 При анализе сточных вол в параллельных пробах получили следующие концентрации марганца (мкг/дм3): 35,9; 38,4; 42,6; 43,9; 35,8; 39,4 и 40,7. Проведите математическую обработку этих результатов. |
