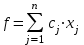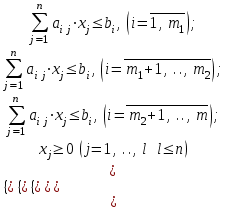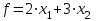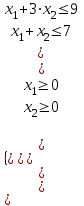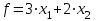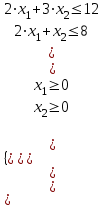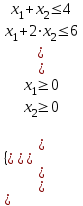Практическая работа 3. Практическая работа 3 Методы оценки качества случайных последовательностей
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
Практическая работа №3 Методы оценки качества случайных последовательностей Цель работы: Научиться применять методы оценки качества случайных последовательностей Теоретические сведения Большое число экономических задач сводится к линейным математическим моделям. Традиционно оптимизационные линейные математические модели называются моделями линейного программирования. Этот термин появился в конце 30-х годов, когда программирование на компьютере еще не было развито, и соответствует не очень удачному переводу английского «programmation». Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана – решения в задачах с линейной структурой. В общем виде задача линейного программирования ставится следующим образом. Максимизировать (минимизировать) функцию:
При ограничениях:
Здесь: 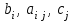 – заданные постоянные величины – заданные постоянные величины 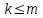 ; ;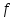 – целевая функция. – целевая функция.Функция (1) называется целевой функцией задачи, а условия (2) – ограничениями задачи. Совокупность чисел ( 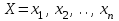 ), удовлетворяющих ограничениям задачи, называется допустимым решением. ), удовлетворяющих ограничениям задачи, называется допустимым решением. Решить задачу линейного программирования значит найти значения управляющих переменных, удовлетворяющих ограничениям (2), при которых целевая функция (1) принимает максимальное (минимальное) значение. Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (система ограничений задачи противоречива) или целевая функция является неограниченной на области определения. Первый случай связан с некорректностями в постановке экономической задачи и (или) разработанной ЭММ. Например, имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т.е. фактически соблюсти принцип альтернативности. Второй случай обычно означает, что ЭММ разработана некорректно, и некоторые существенные ограничения в ней отсутствуют. Задание 1: 1. Составить математическую модель. 2. Ввести на рабочий лист MS Excel условия задачи: а) создать форму на рабочем листе для ввода условий задачи; б) ввести исходные данные, целевую функцию, ограничения и граничные условия. 3. Указать параметры в диалоговом окне Поиск решения. 4. Проанализировать полученные результаты. Рассмотрим решение задачи оптимизации на примере. Задача определения оптимального ассортимента продукции: Предприятие изготавливает два вида продукции – П1 и П2, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 ед. соответственно. Расход сырья на единицу продукции вида П1 и П2 (табл. 1). Таблица 1 Исходные данные
Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 1 ед. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. – для П1 и 4 д. е. – для П2. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? Решение: Построим математическую модель для решения поставленной задачи. Предположим, что предприятие изготовит 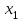 единиц продукции П1 и единиц продукции П1 и 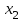 единиц продукции П2. единиц продукции П2. Поскольку производство продукции ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, должны выполняться следующие неравенства: 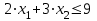 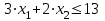 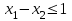 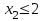 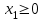 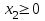 Доход от реализации 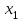 единиц продукции П1 и единиц продукции П1 и 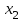 единиц продукции П2 составит единиц продукции П2 составит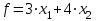 Cреди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция 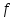 принимает максимальное значения принимает максимальное значения 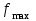 . Рассматриваемая задача относится к разряду типовых задач оптимизации производственной программы предприятия. . Рассматриваемая задача относится к разряду типовых задач оптимизации производственной программы предприятия. В качестве критериев оптимальности в этих задачах могут быть также использованы: прибыль, себестоимость, номенклатура производимой продукции и затраты станочного времени. Создадим на рабочем листе форму для ввода исходных данных. Заливкой выделены ячейки для ввода функций. 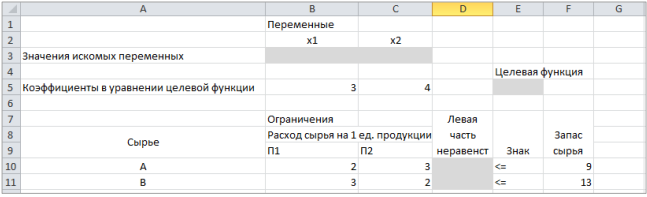 Рисунок 1 – Ввод начальных данных В ячейку E5 введем формулу для целевой функции 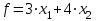 . Используя обозначения соответствующих ячеек в Excel, формулу для расчета целевой функции можно записать как сумму произведений каждой из ячеек, отведенной для значений переменных задачи (B3, C3), на соответствующие ячейки, отведенные для коэффициентов целевой функции (B5, C5). . Используя обозначения соответствующих ячеек в Excel, формулу для расчета целевой функции можно записать как сумму произведений каждой из ячеек, отведенной для значений переменных задачи (B3, C3), на соответствующие ячейки, отведенные для коэффициентов целевой функции (B5, C5).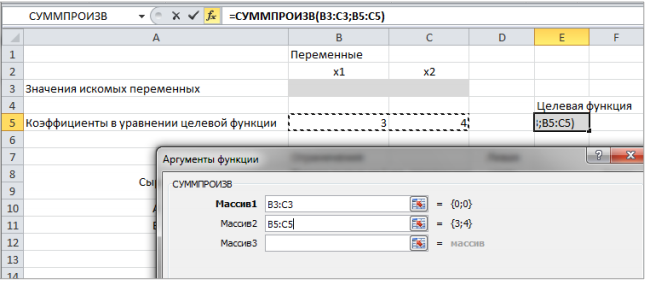 Рисунок 2 – Ввод формулы целевой функции Аналогично в ячейки D10:D11 введены формулы для расчета левой части ограничений: 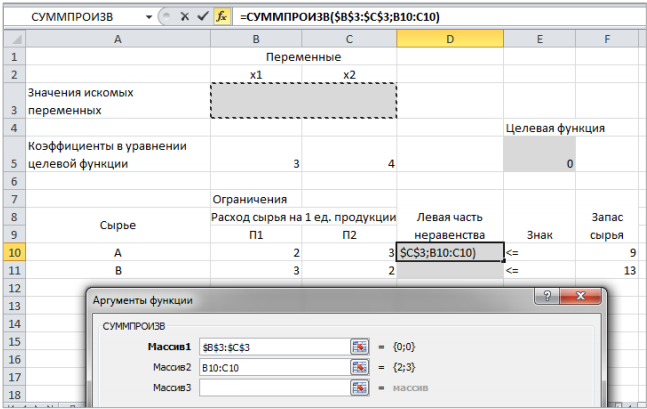 Рисунок 3 – Ввод ограничений На вкладке Данные в группе Анализ выберем команду Поиск решения. В диалоговом окне Параметры поиска решения установим следующее – в поле Оптимизировать целевую функцию выбираем ячейку со значением целевой функции – Е5; – выбираем, максимизировать или минимизировать целевую функцию; – в поле Изменяя ячейки переменных выбираем ячейки со значениями искомых переменных B3:C3 (пока в них нули или пусто); – в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения нашей задачи; – в поле Выберите метод решения указываем Поиск решения линейных задач симплекс-методом; – нажимаем кнопку Найти решение. 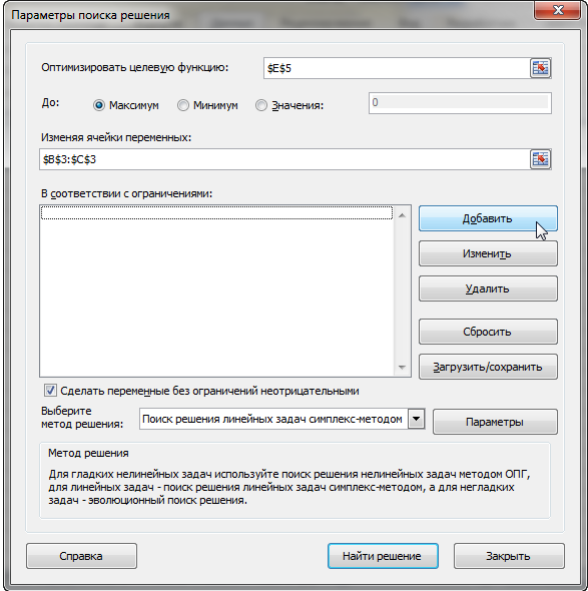 Рисунок 4 – Параметры поиска решения Добавляем ограничения для нашей задачи: 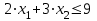 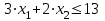 Для неравенств указываем в поле Ссылка на ячейки диапазон D10:D11, выбираем в раскрывающемся списке знак неравенства, в поле Ограничение выделяем диапазон F10:F11 и нажимаем кнопку Добавить, чтобы принять ограничение и добавить следующее ограничение. Для принятия ограничения и возврата к диалоговому окну Поиск решения нажмите кнопку Ok. 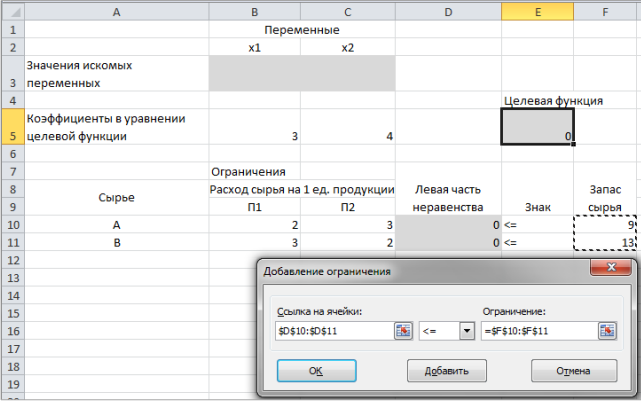 Рисунок 5 – Добавление ограничения Покажем окна для добавления ограничений: 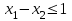 → →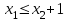 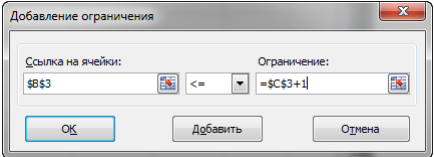 Рисунок 6 – Добавление ограничения 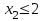 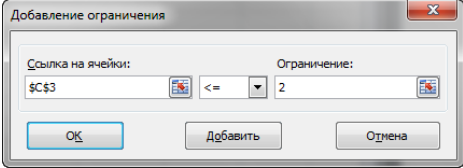 Рисунок 7 – Добавление ограничения 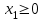 и и 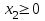 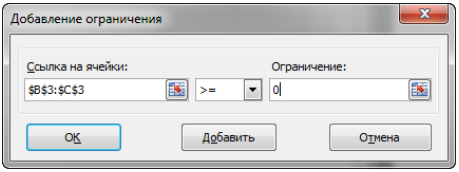 Рисунок 8 – Добавление ограничения После выбора кнопки Найти решение появляется окно Результаты поиска решения:  Рисунок 9 – Результаты поиска решения Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид: 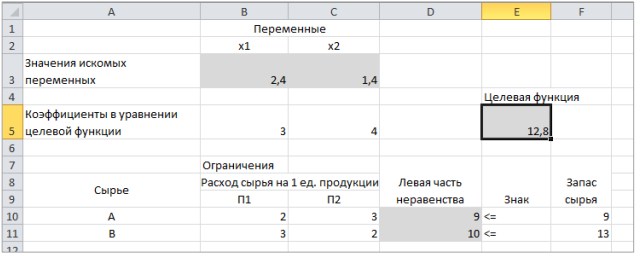 Рисунок 10 – Рабочий лист Сохранить модель поиска решения можно следующим образом: 1) при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения; 2) если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например, найти максимум и минимум одной функции или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Загрузить/Сохранить окна Параметры поиска решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Загрузить/сохранить диалогового окна Параметры поиска решения; 3) сохранить модель можно в виде именованных сценариев, для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений. Кроме вставки оптимальных значений в изменяемые ячейки, Поиск решения позволяет представлять результаты в виде трех отчетов (Результаты, Устойчивость и Пределы). Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них: 1. Отчет по устойчивости содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один – для изменяемых ячеек, а второй – для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. При использовании целочисленных ограничений Excel выводит сообщение Отчеты об устойчивости и Пределы не применимы для задач с целочисленными ограничениями. 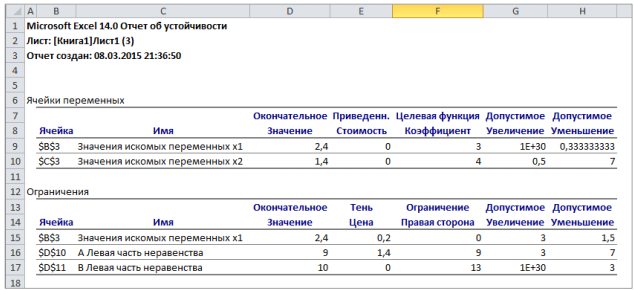 Рисунок 11 – Отчет по устойчивости 2. Отчет по результатам содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй – значения искомых переменных, полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы – это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение – это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение – это ограничение, которое было выполнено с ненулевым значением разницы. 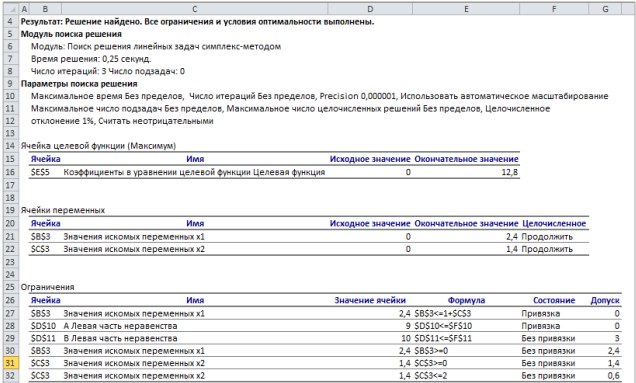 Рисунок 12 – Отчет по результатам 3. Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений. 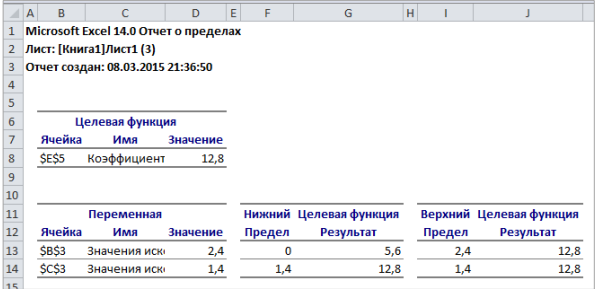 Рисунок 13 – Отчет по пределам Полученное решение означает, что объем производства продукции вида П1 должен быть равен 2,4 ед., а продукции П2 – 1,4 ед. продукции. Доход, получаемый в этом случае, составит 12,8 д. е. Допустим, что к условию задачи добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами. В окне Поиск решения нажмите кнопку Добавить и в появившемся окне Добавление ограничений введите ограничения следующим образом: – в поле Ссылка на ячейки введите адреса ячеек переменных задачи B3:C3; – в поле ввода знака ограничения установите целое; – подтвердите ввод ограничения нажатием кнопки OK. 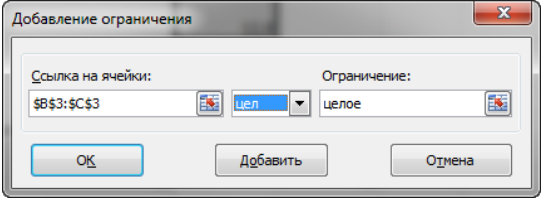 Рисунок 14 – Добавление ограничения Решение задачи при условии целочисленности ее переменных 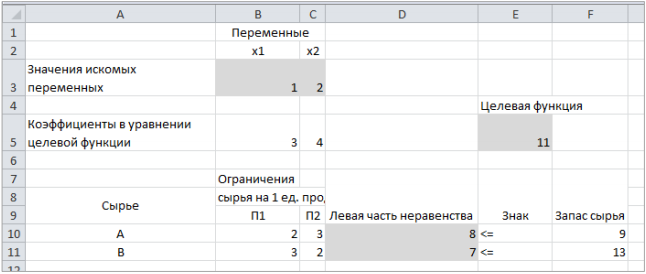 Рисунок 15 – Рабочий лист Задание 2: Найти максимум линейной функции при заданной системе ограничений согласно предложенному преподавателем варианту (табл.2): Таблица 2 Варианты задания
Задание 3: По условию предложенной ниже задачи необходимо выполнить следующие действия: – построить математическую модель задачи; – представить ее в табличной форме на листе Excel; – найти решение задачи средствами надстройки Поиск решения; – вывести отчеты по результатам и устойчивости. Задача: Кондитерская фабрика для производства трех видов карамели А, В, и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида, общее количество сырья каждого вида, прибыль от реализации 1 т карамели: Таблица 3 Исходные данные
Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации. В ответе должно быть получено: максимальная прибыль 162 000 р. при выпуске карамели 100, 0, 1200 т. Задание 4: Сформировать отчет о проделанной работе Контрольные вопросы 1. Каким образом ставится задача линейного программирования? 2. Что включает в себя математическая модель задач условной оптимизации? 3. Расскажите алгоритм решения задач условной оптимизации в MSExcel? 4. Какие отчеты предоставляет Поиск решения? 5. Какую информацию содержит отчет по устойчивости? 6. Какую информацию содержит отчет по результатам? 7. Какую информацию содержит отчет по пределам? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||