ПР 4. Практическая работа 5 Исследование гидродинамики насадочного абсорбера Цель работы

Название	Практическая работа 5 Исследование гидродинамики насадочного абсорбера Цель работы
Дата	27.03.2019
Размер	346.58 Kb.
Формат файла
Имя файла	ПР 4.docx
Тип	Практическая работа #71671

Практическая работа №5

Исследование гидродинамики насадочного абсорбера
Цель работы

1. Ознакомиться с методикой составления математической модели гидродинамики насадочного абсорбера.

2. Практически освоить методику исследования гидродинамики насадочного абсорбера с использованием ячеечной модели.

3. Сравнить экспериментальные и расчетные кривые отклика, проверить модель на адекватность.
Типовые математические модели структуры потоков в аппаратах

Поведение потоков в реальных аппаратах настолько сложно, что в настоящее время дать строгое математическое описание их в большинстве случаев не представляется возможным. В то же время известно, что структура потоков оказывает существенное влияние на эффективность химико-технологических процессов (ХТП), поэтому ее необходимо учитывать при моделировании. При этом математические модели структуры потоков являются основой, на которой строится математическое описание химико-технологического процесса. Точное описание реальных потоков (например, с помощью уравнения Навье – Стокса) приводит к чрезвычайно трудным для решения задачам. Поэтому разработанные к настоящему времени модели структуры потоков в аппаратах являются достаточно простыми и носят полуэмпирический характер. Тем не менее, они позволяют получать математические модели ХТП, достаточно точно отражающие реальный физический процесс (модели, адекватные объекту) [3–5]. Структура математической модели любого процесса химической технологии, в котором происходит перемещение жидкостей или паров, определяется, прежде всего, гидродинамическими параметрами и проявляется в характере распределения времени пребывания частиц потока в рассматриваемой системе.

Этот характер распределения подчиняется статистическим законам и находится по виду сигнала, проходящего через систему. В поток на входе его в аппарат каким-либо способом вводят индикатор, а на выходе потока из аппарата замеряют концентрацию индикатора как функцию времени. Эта выходная кривая называется функцией отклика системы на типовое возмущение по составу потока. Основным требованием, предъявляемым к индикатору, является условие поведения частиц индикатора в аппарате подобно поведению частиц потока.

На практике часто применяют индикаторы, которые не вступают во взаимодействие с основным потоком и могут быть легко замерены.

Индикатор на входе потока в аппарат вводят в виде стандартных сигналов: импульсного, ступенчатого и циклического. В зависимости от вида возмущающего сигнала различают методы исследования структуры потоков: импульсный, ступенчатый и циклический. При ступенчатом изменении входной величины получают соответственно f – выходную кривую (кривую отклика), при нанесении импульсного возмущения получают соответственно С – выходную кривую, при изменении входной величины по законам гармонического колебания получают изменённое по амплитуде и фазе синусоидальное изменение выходной величины.

Статистическая функция распределения индикатора при нанесении импульсного возмущения (С – кривая) записывается в виде [2]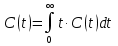

(1)

Функция распределения времени пребывания С(t) характеризует долю индикатора в выходящем потоке.

Среднее время пребывания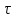

определяется из соотношения

(2)

Функцию распределения С(t) представляют в виде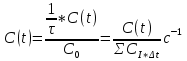

(3)

где t – интервал отбора проб.

Безразмерное время пребывания

(4)

При известном среднем времени пребывания С-кривую можно охарактеризовать уравнением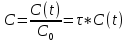

(5)

где С₀ – начальная концентрация вещества на входе.

В зависимости от вида функции распределения все многообразие математических моделей потоков, возникающих в различных аппаратах, может быть представлено в виде некоторых типовых моделей
Модель идеального смешения. Согласно этой модели принимается равномерное распределение субстанции во всем потоке. Зависимость между концентрацией субстанции в потоке на входе и на выходе имеет вид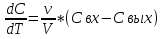

(6)

где

– объемный расход, м³/с;

V – объем аппарата, м³;

С, Свх, Свых – концентрация вещества: текущая, входная, на выходе.

Модель идеального вытеснения. В соответствии с этой моделью принимается поршневое течение без перемешивания вдоль потока при равномерном распределении субстанций в направлении, перпендикулярном движению. Время пребывания в системе всех частиц одинаково и равно отношению объема системы к объемному расходу жидкости.

Математическое описание модели имеет вид

(7)

где u – линейная скорость потока, м/с.

Диффузионные модели. Различают однопараметрическую и двухпараметрическую диффузионные модели.

Однопараметрическая модель. Ее основой является модель идеального вытеснения, осложненная обратным перемешиванием, подчиняющимся формальному закону диффузии. Параметром, характеризующим модель, служит коэффициент турбулентной диффузии, или коэффициент продольного перемешивания D_L.

При составлении однопараметрической диффузионной модели принимаются следующие допущения:

изменение концентрации субстанции является непрерывной функцией пространственной координаты;
концентрация субстанции в данном сечении постоянна;
объемная скорость потока и коэффициент перемешивания не изменяются по длине и сечению потока.

При таких допущениях модель описывается уравнением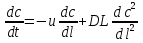

(8)

Член уравнения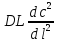

учитывает турбулентную диффузию, или продольное перемешивание. Величина D_Lопределяется расчетным или опытным путем.

Двухпараметрическая модель. В этой модели учитывается перемешивание потока в продольном и радиальном направлениях; причем модель характеризуется коэффициентом продольного (D_L) и радиального (D_R) перемешивания. При этом принимается, что величины D_Lи D_Rне изменяются по длине и сечению аппарата, а скорость потока постоянна.

При условии движения потока в аппарате цилиндрической формы радиуса R с постоянной по длине и сечению скоростью уравнение двухпараметрической модели имеет вид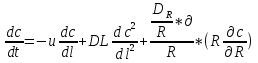

(9)

При опытном определении коэффициентов продольного и радиального перемешивания (D_Lи D_R) обычно их представляют в виде безразмерных комплексов – критериев Пекле: P_e_Д=u*L/D_L или P_e=u*L/D_R, где L – определяющий линейный размер системы. Тогда уравнение диффузионной модели также приводится к безразмерному виду. С этой целью вводятся безразмерная концентрация C=c/c₀; безразмерная длина z=l/L и время =L/u=V/.

Учитывая, что объемная скорость принимается постоянной, для установившегося режима уравнение (8) приводится к виду

(10)

Если P→∞, диффузионная модель переходит в модель идеального вытеснения; если P→0– в модель идеального перемешивания.

Ячеечная модель. Основой модели является представление об идеальном перемешивании в пределах ячеек, расположенных последовательно, и в отсутствии перемешивания – между ячейками. Параметром, характеризующим модель, служит число ячеек N.

Математическое описание ячеечной модели включает N линейных дифференциальных уравнений первого порядка: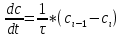

где i =1, 2, ..., N (N – номер ячейки);

 – время контакта.

Ячеечной моделью оценивают функции распределения в последовательно соединенных аппаратах с мешалками, осуществляющими интенсивное перемешивание.

Кривые отклика при ступенчатом или импульсном возмущении для различных типов гидродинамических моделей представлены в табл. 2.1.

Таблица 2.1

Типовые модели структуры потоков в аппарате

$c:\users\марианна\appdata\local\microsoft\windows\inetcache\content.word\новый рисунок (3).bmp$

Математическое описание гидродинамики насадочного абсорбера
Абсорбцией называется процесс поглощения газа или пара жидким поглотителем (абсорбентом). В промышленности абсорбция с последующей десорбцией широко применяется для выделения из газовых смесей ценных компонентов (например, для извлечения из коксового газа аммиака, бензола и др.), для очистки технологических и горючих газов от вредных примесей (например, для очистки отходящих газов от сернистого ангидрида) и т. д. [11–14].

При абсорбции процесс массопередачи протекает на поверхности соприкосновения фаз. Поэтому в аппаратах для поглощения газов жидкостями (абсорберах) должна быть создана развитая поверхность соприкосновения между газом и жидкостью. Скорость массопередачи в насадочном абсорбере зависит от гидродинамического режима в аппарате.

Насадочные абсорберы представляют собой колонны, загруженные насадкой – твердыми телами различной формы – для увеличения поверхности соприкосновения между газом и жидкостью (рис. 2.1).

$c:\users\марианна\appdata\local\microsoft\windows\inetcache\content.word\новый рисунок (5).bmp$
Жидкость стекает по поверхности насадки тонкой пленкой и одновременно распределяется в слое насадки в виде капель и брызг.

Насадка 1 опирается на решетку 2, в которой имеются отверстия для прохода газа и стока жидкости. Газ поступает в колонну снизу и движется вверх противотоком по отношению к жидкости.

Типовые модели идеального перемешивания, идеального вытеснения, диффузионная модель с определенной степенью точности могут применяться для воспроизведения структуры и гидродинамических свойств потоков в различных аппаратах химической технологии. Однако идеальные модели в ряде случаев неадекватны реальному процессу, а диффузионная модель отличается сложностью. По этой причине для трубчатых и колонных аппаратов удобнее представлять реальные потоки в виде ячеечной модели [5]. Построим математическую модель гидродинамики насадочного абсорбера по газовому потоку. Для этого разобьем насадку на N ячеек (рис. 2.2) и запишем систему дифференциальных уравнений (2.12).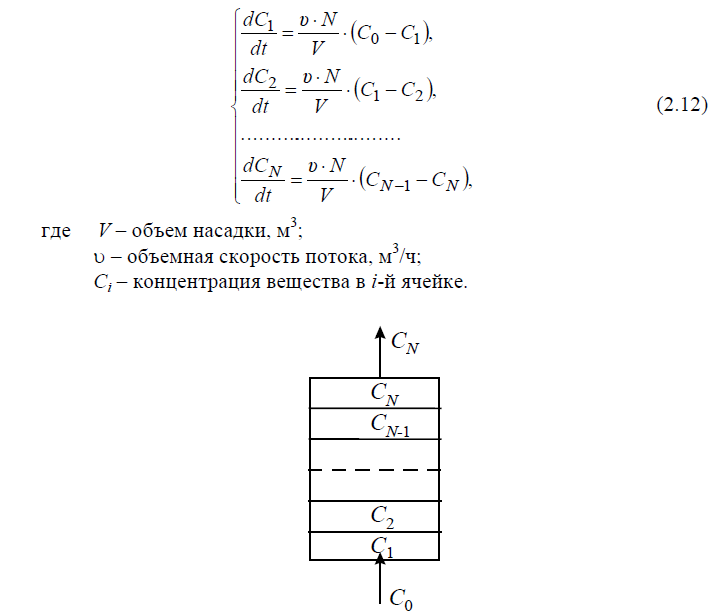

$c:\users\марианна\appdata\local\microsoft\windows\inetcache\content.word\новый рисунок (6).bmp$
Рис. 2.2. Ячеечная схема насадки

$c:\users\марианна\appdata\local\microsoft\windows\inetcache\content.word\новый рисунок (7).bmp$
$c:\users\марианна\appdata\local\microsoft\windows\inetcache\content.word\новый рисунок (8).bmp$

$c:\users\марианна\appdata\local\microsoft\windows\inetcache\content.word\новый рисунок (9).bmp$

Порядок выполнения работы

1. Ознакомиться с методикой моделирования гидродинамики насадочного абсорбера.

2. Ознакомиться со структурной схемой алгоритма исследования гидродинамики насадочного абсорбера.

3. Подготовить исходные данные.

4. Разработать программу и выполнить расчеты при различных значениях числа ячеек (N).

5. Выбрать оптимальное число ячеек.

6. Обсудить результаты. Сделать выводы по работе.
Содержание отчета

Отчет по лабораторной работе должен содержать следующие разделы:

1. Цель работы.

2. Описание методики моделирования гидродинамики насадочного абсорбера.

3. Исходные данные.

4. Программу и результаты расчета.

5. Анализ результатов расчета и выводы.

Контрольные вопросы и задания

1. Какие гидродинамические модели вы знаете?

2. Какие методы применяются для определения гидродинамической структуры потоков в аппаратах?

3. Назовите основные типовые возмущения.

4. Что такое кривая отклика?

5. Назовите основные параметры ячеечной гидродинамической модели.

6. Какие данные необходимы для проверки модели на адекватность?
Список литературы
1. Панченков Г. М., Лебедев В. П. Химическая кинетика и катализ. – М.: Химия, 1985. – 589 с.

2. Яблонский Г. С., Быков В. И., Горбань А. И. Кинетические модели каталитических реакций. – Новосибирск: Наука, 1983. – 254 с.

3. Кафаров В. В. Методы кибернетики в химии и химической технологии. – М.: Химия, 1988. – 489 с.

4. Кравцов А. В., Новиков А. А., Коваль П. И. Методы анализа химико-технологических процессов. – Томск: изд-во ТПУ, 1994. – 76 с.

5. Кафаров В. В., Глебов М. В. Математическое моделирование основных процессов химических производств. – М.: Высш. шк., 1991. – 400 с.

6. Мойзес О. Е., Коваль П. И., Баженов Д. А., Кузьменко Е. А. Информатика: учеб. пособие. В 2-х ч. – Томск, 1999. – 150 с.

7. Турчак Л. И. Основы численных методов. – М.: Наука, 1987. – 320 с.

8. Офицеров Д. В., Старых В. А. Программирование в интегрированной среде Турбо-Паскаль. – Минск: Беларусь, 1992. – 240 с.

9. Бесков В. С., Флор К. В. Моделирование каталитических процессов и реакторов. – М.: Химия, 1991. – 252 с.

10. Руд Р., Праустниц Дж., Шервуд Т. Свойства газов и жидкостей / под ред. Б. И. Соколова. – Л.: Химия, 1982. – 591 с.

11. Танатаров М. А. и др. Технологические расчеты установок переработки нефти. – М.: Химия, 1987. – 350 с.

12. Жоров Ю. М. Термодинамика химических процессов. – М.: Химия, 1985. – 458 с.

13. Расчеты основных процессов и аппаратов нефтепереработки: справочник / под ред. Е. Н. Судакова. – М.: Химия, 1979. – 568 с.

14. Кафаров В. В. Разделение многокомпонентных систем в химической технологии. Методы расчета. – М.: Московский химико-технологический институт, 1987. – 84 с.
Программа расчета гидродинамики насадочного абсорбера

Обозначения, принятые в программе:

Ha – высота абсорбера, м;

S – площадь поперечного сечения абсорбера, м2;

V – объёмный расход исходной газовой смеси, м3/ч;

C0 – концентрация извлекаемого компонента в исходной газовой смеси, моль/л;

N – число ячеек в модели;

tau – время пребывания, с;

С – массив концентраций внутри ячеек;

Сe – массив экспериментальных значений концентраций на кривой отклика, моль/л;

Сr – массив расчетных значений концентраций на кривой отклика, моль/л;

tk – время переходного процесса, с;

t – текущее время, c;

h – шаг интегрирования;

F – массив сумм квадратов отклонений расчетных значений концентраций на кривой отклика от экспериментальных;

Fmin – минимальное значение суммы квадратов отклонений расчетных значений концентраций на кривой отклика от экспериментальных;

N0 – оптимальное число ячеек.
Program absor;

Type mas=array[1..10] of real;

const Ha=11.5;S=1.8;V=10000.0;C0=0.18;h=1;

Ce:mas=(0.002,0.05,0.1,0.12,0.14,0.15,0.155,0.159,0.161,0.166);

var Cr,F:mas;

C:array[0..10]of real;

tau,Fmin:real;

i,N,N0,t:integer;

f1:text;

begin

assign(f1,'rabsor.pas');

rewrite(f1);

tau:=Ha*S/V*3600;

Writeln(f1,'Расчет гидродинамики абсорбера');

for N:=1 to 10 do

begin

C[0]:=C0;

for i:=1 to N do

C[i]:=0;

F[N]:=0;

for t:=1 to 10 do

begin

for i:=1 to n do

C[i]:=C[i]+h*N/tau*(C[i-1]-C[i]);

Cr[t]:=C[N];

F[N]:=F[N]+sqr(Ce[t]-Cr[t]);

end;

end;

Fmin:=F[1];

N0:=1;

For i:=2 to 10 do

if F[i]
begin

Fmin:=F[i];

N0:=i;

end;

C[0]:=C0;

for i:=1 to N0 do

C[i]:=0;

writeln(f1,'Оптимальное число ячеек N=',N0, '.. Fmin=', Fmin:11);

Writeln(f1,'Время,с Сэкс Срасч');

for t:=1 to 10 do

begin

for i:=1 to n0 do

C[i]:=C[i]+h*N0/tau*(C[i-1]-C[i]);

Cr[t]:=C[N0];

writeln(f1,t:4,Ce[t]:9:3,Cr[t]:9:3);

end;

close(f1);

end.